Class 11 RD Sharma Solutions – Chapter 30 Derivatives – Exercise 30.2 | Set 2
Last Updated :
30 Apr, 2021
Question 3. Differentiate each of the following using first principles:
(i) xsinx
Solution:
Given that f(x) = xsinx
By using the formula

We get
= 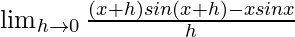
= 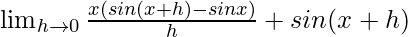
Using the formula
sinc – sind = 2cos((c + d)/2)sin((c – d)/2)
We get
= 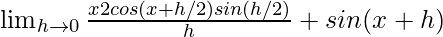
As we know that 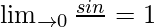
So,
= 2x × cosx × 1/2 + sinx
= x × cosx + sinx
= sinx + xcosx
(ii) xcosx
Solution:
Given that f(x) = xcosx
By using the formula
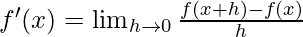
We get
= 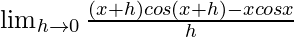
= 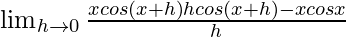
= 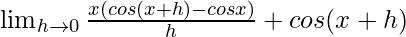
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}x.2sin(x-x+h/2)sin(x+h/2)+cos(x+h) [cosA-cosB=2sin(\frac{B-A}{2})sin(\frac{B+A}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d6447bf9b23ed3075f5fed9dfc40a65f_l3.png)
= 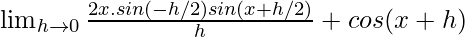
= -xsinx + cosx
(iii) sin(2x – 3)
Solution:
Given that f(x) = sin(2x – 3)
By using the formula

We get
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{sin[2(x+h)-3]-sin(2x-3)}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c9ad651a4aca5d5e94e09e205cdf938_l3.png)
= 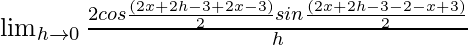
Using the formula
sinC – sinD = 2cos{C+D}/2sin{C-D}/2
= 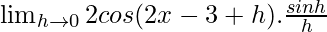
As we know that, \lim_{θ\to 0}\frac{sinθ}{θ}=1 so,
= 2cos(2x – 3)
(iv) √sin2x
Solution:
Given that f(x) = √sin2x
By using the formula

We get
= 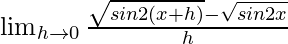
On multiplying numerator and denominator by 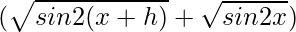
we get
= 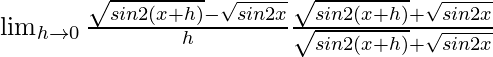
= 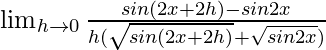
= 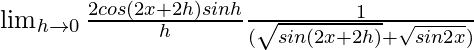
= 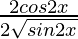
= 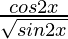
(v) sinx/x
Solution:
Given that f{x} = sinx/x
By using the formula

We get
= 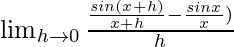
= 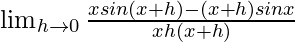
= 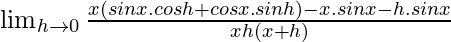
= 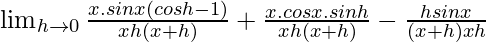
= 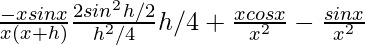
h ⇢ 0 ⇒ h/2 ⇢ 0 and 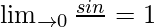
= 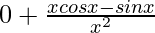
=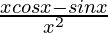
(vi) cosx/x
Solution:
Given that f(x) = cosx/x
By using the formula

We get
= 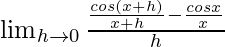
= 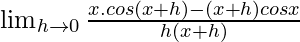
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{x[cosx.cosh-sinx.sinh]-x.cos-h.cosx}{h(x+h)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8228a5a7381eb39a60144755f9009ca_l3.png)
= 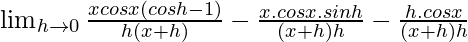
= 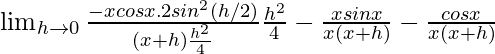
= 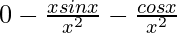
= 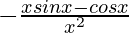
(vii) x2sinx
Solution:
Given that f(x) = x2sinx
By using the formula

We get
= 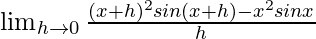
= 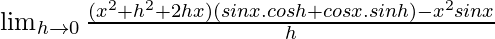
= 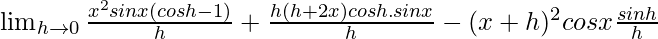
= 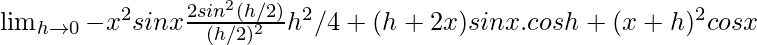
= 0 + [2xsinx + x2cosx]
= 2xsinx + x2cosx
(viii) 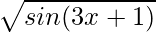
Solution:
Given that f(x) = 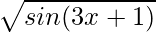
By using the formula

We get
= 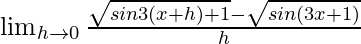
= 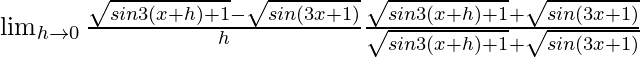
= 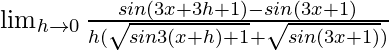
= 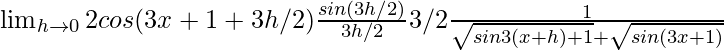
= 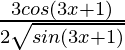
(ix) sinx + cosx
Solution:
Given that f(x) = sinx + cosx
By using the formula

We get
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[sin(x+h)+cos(x+h)]-sinx+cosx}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b975cc2fd34f42f6b5939f9373d7be96_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[sin(x+h)+cos(x+h)-sinx-cosx]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f2c640ab276424ba6973601cf297f17_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[sin(x+h)-sinx]+[cos(x+h)-cosx]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-930550f4f50501870a5778147f0b1e62_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[2sin\frac{x+h-x}{2}cos\frac{x+h+x}{2}]+[-2sin\frac{x+h+x}{2}sin\frac{x+h-x}{2}]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7f03ddea682e951d43f1f4c41a419465_l3.png)
= 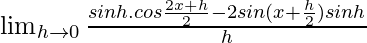
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{sinh}{h}[cos\frac{x+h}{2}-sin(x+\frac{h}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-185ed9f000845c5d27ddb1c7f83052cd_l3.png)
= cosx – sinx
Question 4. Differentiate each of the following using first principles:
(i) tan2x
Solution:
Given that f(x) = tan2x
By using the formula

We get
= 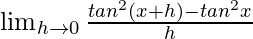
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[tan(x+h)+tanx][tan(x+h)-tanx]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e1bb45d8d907e404353d1ed5651d09ea_l3.png)
= 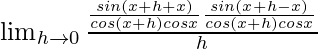
= 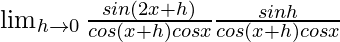
= 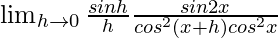
= 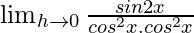
= 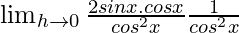
= 2tanx sec2x
(ii) tan(2x + 1)
Solution:
Given that f(x) = tan(2x+1)
By using the formula

We get
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{tan[2(x+h)+1]-tan(2x+1)}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-96cd2f37dba91c97d753e0e5faefa3c4_l3.png)
= 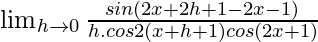
= 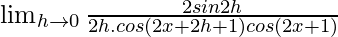
Multiplying both, numerator and denominator by 2.
= 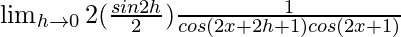
= 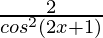
= 2sec2(2x+1)
(iii) tan2x
Solution:
Given that f(x) = tan2x
By using the formula

We get
= 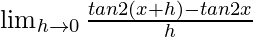
= 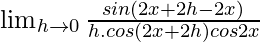
= 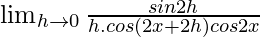
= 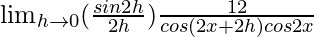
= 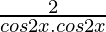
= 2sec22x
(iv) √tanx
Solution:
Given that f(x) = √tanx
By using the formula

We get
= 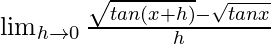
On multiplying numerator and denominator by 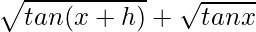
We get
= 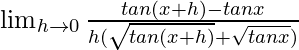
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{sin(x+h-x)}{h.cos(x+h)cosx[\sqrt{tan(x+h)}+\sqrt{tanx}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-786cfa2381a724019862fee1051fcf1b_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{sinh}{h}×\frac{1}{cos(x+h)cosx[\sqrt{tan(x+h)}+\sqrt{tanx}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8105327cd954fc85b014164041f8d2c3_l3.png)
= 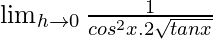
= 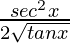
Question 5. Differentiate each of the following using first principles:
(i) 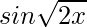
Solution:
Given that f(x) = 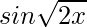
By using the formula

We get
= 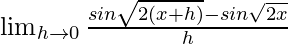
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{2sin[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]cos[\frac{\sqrt{2(x+h)}+\sqrt{2x}}{2}]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c807e1f9a661ef7d3e0a18a36db46f1_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{sin[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}{[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}\frac{(\sqrt{2(x+h)}-\sqrt{2x})(\sqrt{2(x+h)}+\sqrt{2x})}{(\sqrt{2(x+h)}+\sqrt{2x})h}cos[\frac{\sqrt{2(x+h)+2x}}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8c36845e81daadfdc771f002c7c8e066_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{sin[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}{[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}\lim_{h\to 0}\frac{{2(x+h)}-2x}{(\sqrt{2(x+h)}+\sqrt{2x})h}\lim_{h\to 0}cos[\frac{\sqrt{2(x+h)+2x}}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5d2c2901d1934e9a32e8b08649358bfe_l3.png)
= 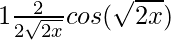
= 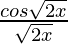
(ii) cos√x
Solution:
Given that f(x) = cos√x
By using the formula

We get
= 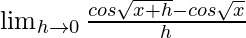
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{-2sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}].sin[\frac{\sqrt{x+h}-\sqrt{x}}{2}]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c0d8dc252558369fd2311d1286b8bd12_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{-2sin[\frac{\sqrt{x+h}-\sqrt{x}}{2}][\sqrt{x+h}-\sqrt{x}[\sqrt{x+h}+\sqrt{x}]}{h[\frac{\sqrt{x+h}-\sqrt{x}}{2}][\sqrt{x+h}+\sqrt{x}]}×sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bf72051f52d104bd445cf8108a0a2416_l3.png)
Multiplying numerator and denominator by 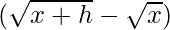
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{-sin[\frac{\sqrt{x+h}-\sqrt{x}}{2}]}{[\frac{\sqrt{x+h}-\sqrt{x}}{2}]}×\frac{x+h-x}{(\sqrt{x+h}+\sqrt{x})h}×sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c45b9cee19296e3a43860e921c03c742_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}-1\frac{h}{(\sqrt{x+h}+\sqrt{x})h}×sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cbbadee781ca185484b55c164bef676b_l3.png)
= 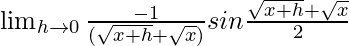
= 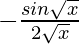
(iii) tan√x
Solution:
Given that f(x) = tan√x
By using the formula

We get
= 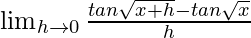
= 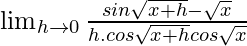
= 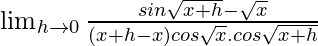
= 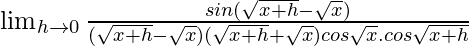
= 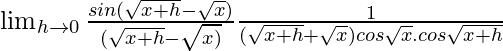
= 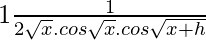
= 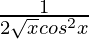
= 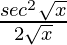
(iv) tanx2
Solution:
Given that f(x) = tanx2
By using the formula

We get
= 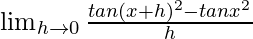
= 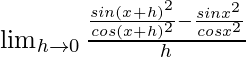
= 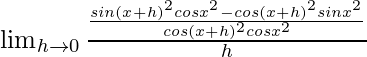
= 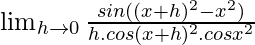
= 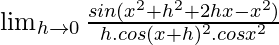
= 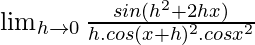
= 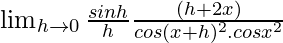
= 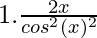
= 2xsec2x2
Question 6. Differentiate each of the following using first principles:
(i) -x
Solution:
Given that f(x) = -x
By using the formula

We get
= 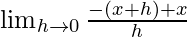
= 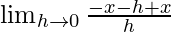
= -1
(ii) (-x)-1
Solution:
Given that f(x) = (-x)-1
By using the formula

We get
= 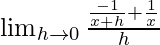
= 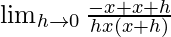
= 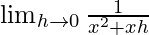
= 1/x2
(iii) sin(x + 1)
Solution:
Given that f(x) = sin(x+1)
By using the formula

We get
= 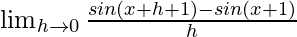
= 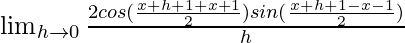
= 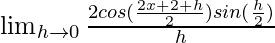
= 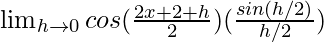
= 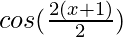
= cos(x+1)
(iv) cos(x – π/8)
Solution:
We have, f(x) = cos(x – π/8)
By using the formula

We get
= 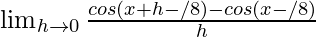
= 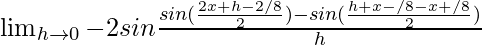
= 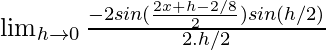
= 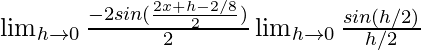
= 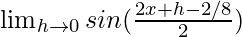
= 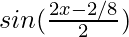
= -sin(x + π/8)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...