Class 11 RD Sharma Solutions – Chapter 30 Derivatives – Exercise 30.2 | Set 1
Last Updated :
30 Apr, 2021
Question 1. Differentiate each of the following using first principles:
(i) 2/x
Solution:
Given that f(x) = 2/x
By using the formula
f'(x) = 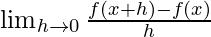
We get
= 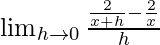
= 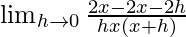
= 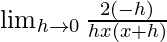
= 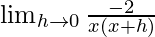
= 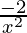
(ii) 1/√x
Solution:
Given that f(x) = 1/√x
By using the formula

We get
= 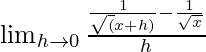
= 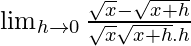
= 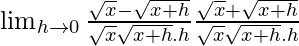
= 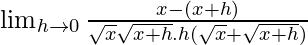
= 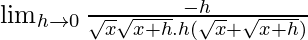
= 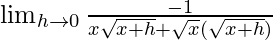
= 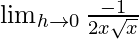
= 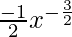
(iii) 1/x3
Solution:
We have f(x) = 1/x3
By using the formula

We get
= 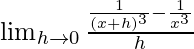
= 
= 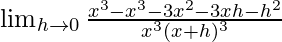
= 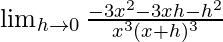
= 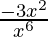
= 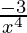
(iv) (x2 + 1)/x
Solution:
Given that f(x) = (x2 + 1)/x
By using the formula

We get
= 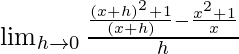
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{x[x^2+h^2+2xh+1]-(x^2+1)(x+h)}{hx(x+h)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c0d0cb61a2d84509a3b0d090b5051131_l3.png)
= 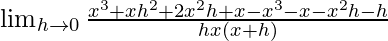
= 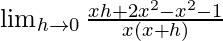
= 
= 
(v) (x2 – 1)/x
Solution:
Given that f(x) = (x2 – 1)/x
By using the formula

We get
= 
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{x[x^2+h^2+2xh-1]-(x^2-1)(x+h)}{hx(x+h)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bcb7bc926a3f794bb402d90d6d776cdd_l3.png)
= 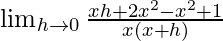
= 
= 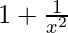
(vi) (x + 1)/(x + 2)
Solution:
Given that f(x) = (x + 1)/(x + 2)
By using the formula

We get
= 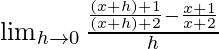
= 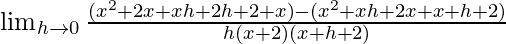
= 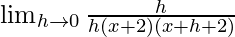
= 1/(x + 2)2
(vii) (x + 2)/(3x + 5)
Solution:
Given that f(x) = (x + 2)/(3x + 5)
By using the formula

We get
= 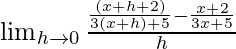
= 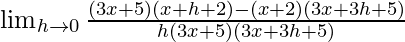
= 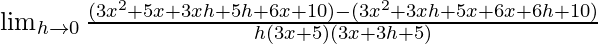
= 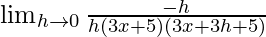
= 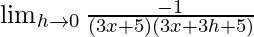
= 
(viii) kxn
Solution:
Given that f(x) = kxn
By using the formula

We get
= 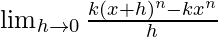
= 
= 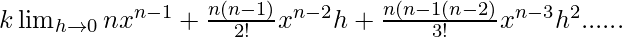
= k nxn-1+ 0 + 0 …
= k nxn-1
(ix) 1/√(3 – x)
Solution:
Given that f(x) = 1/√(3-x)
By using the formula

We get
= 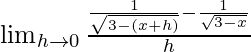
= 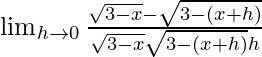
= 
= 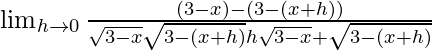
= 
= 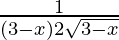
= 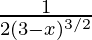
(x) x2 + x + 3
Solution:
Given that f(x) = x2 + x + 3
By using the formula

We get
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[(x+h)^2+(x+h)+3]-x^2+x+3}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0719ad319289ea333c92102b3f64ce6b_l3.png)
= 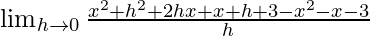
= 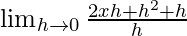
= 
= 2x + 0 + 1
= 2x + 1
(xi) (x + 2)3
Solution:
Given that f(x) = (x + 2)3
By using the formula

We get
= 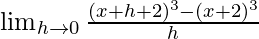
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[(x+2)+h]^3-(x+2)^3}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2da833d869c86e1839399481545b3d52_l3.png)
= 
= 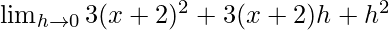
= 3(x + 2)2
(xii) x3 + 4x2 + 3x + 2
Solution:
Given that f(x) = x3 + 4x2 + 3x + 2
By using the formula

We get
= 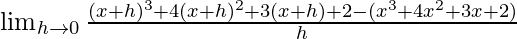
= 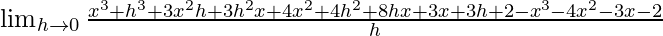
= 
= 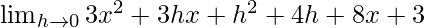
= 3x2 + 8x + 3
(xiii) (x2 + 1)(x – 5)
Solution:
Given that f(x) = (x2+1)(x-5)
By using the formula

We get
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[(x+h)^3+(x+h)-5(x+h^2)-5]-(x^3-5x^2+x-5)}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dc6be2b4ec49ad59f0ff3bc2a8511281_l3.png)
= 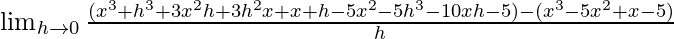
= 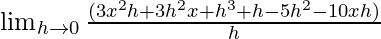
= 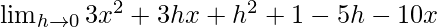
= 3x2 – 10x + 1
(xiv) √(2x2 + 1)
Solution:
Given that f(x) = √(2x2 + 1)
By using the formula

We get
= 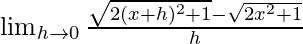
On multiplying numerator and denominator by 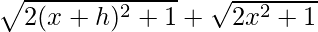
We get
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[2(x+h)^2+1-(2x^2+1)]}{h(\sqrt{2(x+h)^2+1}+\sqrt{2x^2+1})}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-262a4e3c9adb0003bad1d8ea9dfcdf92_l3.png)
= 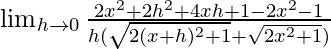
= 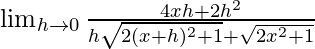
= 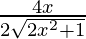
= 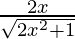
(xv) (2x + 3)/(x – 2)
Solution:
Given that f(x) = (2x + 3)/(x – 2)
By using the formula

We get
= 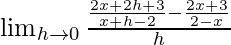
= 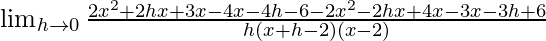
= 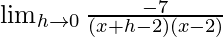
= 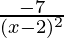
Question 2. Differentiate each of the following using first principles:
(i) e-x
Solution:
Given that f(x) = e-x
By using the formula

We get
= 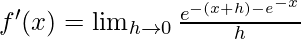
= 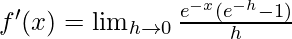
= 
= -e-x
(ii) e3x
Solution:
Given that f(x) = e3x
By using the formula

We get
= 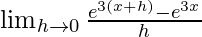
= 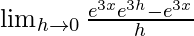
= 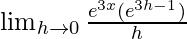
Multiplying numerator and denominator by 3.
= 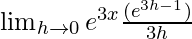
Here, 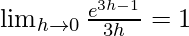
= 3e3x
(iii) eax+b
Solution:
Given that f(x) = eax+b
By using the formula

We get
= 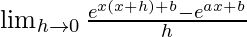
= 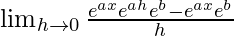
= 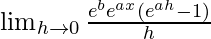
= 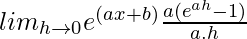
On multiplying numerator and denominator by a
Since 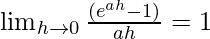
= aeax+b
(iv) xex
Solution:
Given that f(x) = xex
By using the formula

We get
= 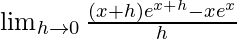
= 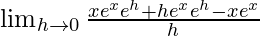
= 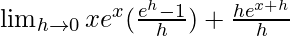
= xex + ex
= ex(x + 1)
(v) x2 ex
Solution:
Given that f(x) = x2ex
By using the formula

We get
= 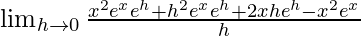
= 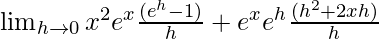
= x2ex + ex(0 + 2x)
= x2ex + 2xex
= ex(x2 + 2x)
(vi) 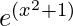
Given that f(x) = 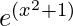
By using the formula

We get
= 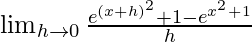
= 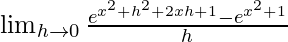
= 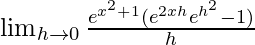
= 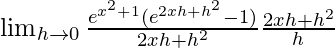
= 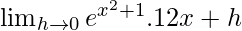
= 
(vii) e√(2x)
Solution:
Given that f(x) = 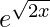
By using the formula

We get
= 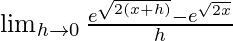
= 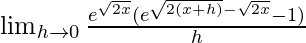
= 
On multiplying numerator and denominator by 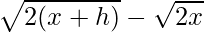
we get
= 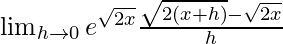
Again multiplying numerator and denominator by 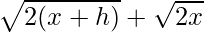
we get
= 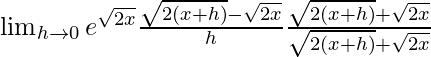
= 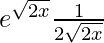
(viii) e√(ax + b)
Solution:
Given that f(x) = e√(ax+b)
By using the formula

We get
= 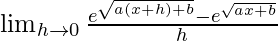
= 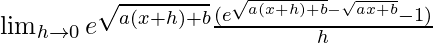
= 
On multiplying numerator and denominator by 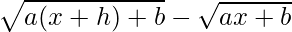
we get
= 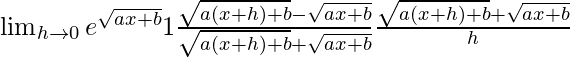
Again multiplying numerator and denominator by 
we get
= 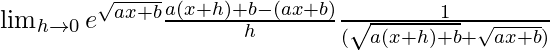
= 
= 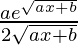
(ix) a√x
Solution:
Given that f(x) = a√x = e√xloga
By using the formula

We get
= 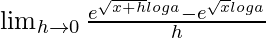
= 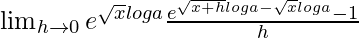
= 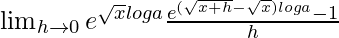
On multiplying numerator and denominator by 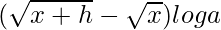
we get
f”(x) = 
= 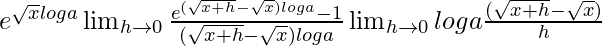
= 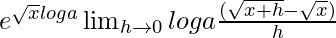
On multiplying numerator and denominator by 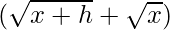
we get
f'(x) = 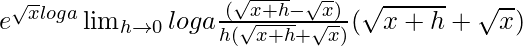
= 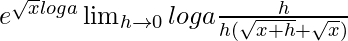
= 
= 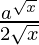 logea
logea
(x) 
Solution:
Given that f(x) = 
By using the formula

We get
= 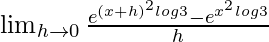
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}e^{x^2log3}\frac{[e({(x+h)^2-x^2)^{log3}}-1]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-30154b123d388b9b4e6a78170e426c64_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to 0}e^{x^2log3}\frac{[e{(x+h)^2-x^2]^{log3}}-1}{(x+h)^2-x^2}×\frac{(x+h)^2-x^2}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-348e0d2caa309b8145b67a456a818307_l3.png)
= 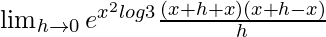
= 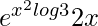
= 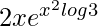
= 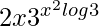
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...