Skip to content
Related Articles
Get the best out of our app
GeeksforGeeks App
Open App
geeksforgeeks
Browser
Continue

Related Articles

Class 11 RD Sharma Solutions- Chapter 30 Derivatives – Exercise 30.1

Improve Article
Save Article
Like Article
author
manandeep1610
scholar
57 published articles
Improve Article
Save Article
Like Article

Question 1. Find the derivative of f(x) = 3x at x = 2

Solution:

Given: f(x)=3x

By using the derivative formula,

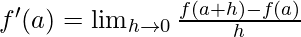f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {where h is a small positive number}

Derivative of f(x)=3x at x=2 is given as:

f'(2)= \lim_{h \to 0} \frac {f(2+h)-f(2)} h

⇒ f'(2)= \lim_{h \to 0} \frac {3(2+h)-3(2)} h

⇒ f'(2)= \lim_{h \to 0} \frac {3h+6-6} h

⇒ f'(2)= \lim_{h \to 0} \frac {3h} h

⇒ f'(2)= \lim_{h \to 0} 3 = 3

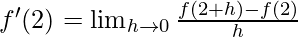
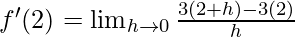
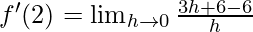
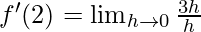
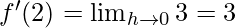
Hence, derivative of f(x)=3x at x=2 is 3

Question 2. Find the derivative of f(x) = x2– 2 at x = 10

Solution:

Given: f(x)= x2-2 

By using the derivative formula,

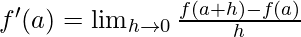f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {where h is a small positive number}

Derivative of f(x)=x2-2 at x=10 is given as:

f'(10)= \lim_{h \to 0} \frac {f(10+h)-f(10)} h

⇒f'(10)= \lim_{h \to 0} \frac {(100+h^2+20h-2-100+2))} h

⇒f'(10)= \lim_{h \to 0} \frac {h^2+20h} h

⇒f'(10)= \lim_{h \to 0} \frac {h(h+20)} h

⇒f'(10)= \lim_{h \to 0} {h+20}

⇒f'(10)= 0+20=20

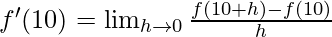
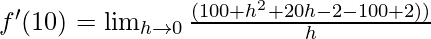
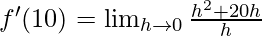
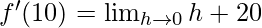
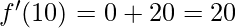
Hence, derivative of f(x)=x2-2 at x=10 is 20

Question 3. Find the derivative of f(x) = 99x at x = 100

Solution:

Given: f(x)= 99x

By using the derivative formula,

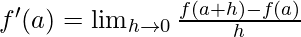f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {where h is a small positive number}

Derivative of f(x)=99x at x=100 is given as:

f'(100)= \lim_{h \to 0} \frac {f(100+h)-f(100)} h

⇒ f'(100)= \lim_{h \to 0} \frac {99(100+h)-99(100)} h

⇒ f'(100)= \lim_{h \to 0} \frac {9900+99h-9900} h

⇒ f'(100)= \lim_{h \to 0} 99 = 99

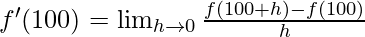
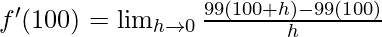
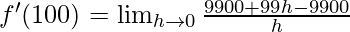
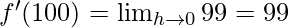
Hence, derivative of f(x)=99x at x=100 is 99

Question 4. Find the derivative of f(x) = x at x = 1

Solution:

Given: f(x)=x

By using the derivative formula,

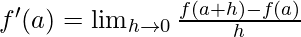f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h {where h is a small positive number}

Derivative of f(x)=x at x=1 is given as:

f'(1)= \lim_{h \to 0} \frac {f(1+h)-f(1)} h

⇒ f'(1)= \lim_{h \to 0} \frac {(1+h)-1} h

⇒ f'(1)= \lim_{h \to 0} \frac {h} h

⇒f'(1)= \lim_{h \to 0} 1 = 1

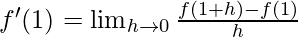
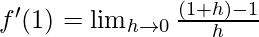
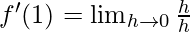
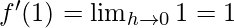
Hence, derivative of f(x)=x at x=1 is 1

Question 5. Find the derivative of f(x) = 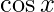\cos x  at x = 0

Solution:

Given: f(x)=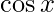\cos x

By using the derivative formula,

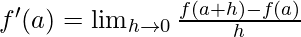f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h {where h is a small positive number}

Derivative of f(x)=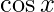\cos x  at x=0 is given as:

f'(0)= \lim_{h \to 0} \frac {f(0+h)-f(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\cos(0+h)-\cos(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\cos(h)-\cos(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\cos(h)-1} h

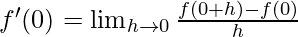
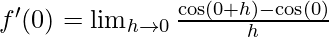
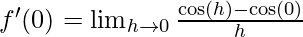
∵ we can not find the limit of the above function f(x)=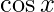\cos x  by direct substitution as it gives 0/0 form (indeterminate form)

So we will simplify it to find the limit.

As we know that 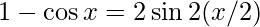1 - \cos x = 2 \sin2(x/2)

∴ f'(0)= \lim_{h \to 0} \frac {-(1-\cos(h))} h = - \lim_{h \to 0} \frac {2\sin^2(h/2)} h

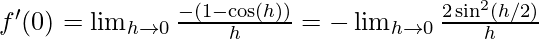
Divide the numerator and denominator by 2 to get the form 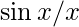\sin x/x  for applying sandwich theorem and multiplying h in numerator and denominator to get the required form.

⇒ f'(0)= -\lim_{h \to 0}( \frac {\frac {2\sin^2(h/2)}2} {\frac {h^2}2}) \times h

⇒ f'(0)= -\lim_{h \to 0}( \frac {\sin(h/2)} {\frac {h}2}) \times \lim_{h \to 0}h

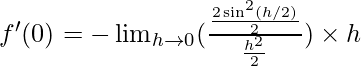
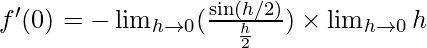
Using the formula: \lim_{x \to 0} \frac{\sin x}x=1

∴ f'(0)=-1 \times 0=0

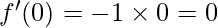
Hence, derivative of f(x)=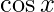\cos x  at x=0 is 0

Question 6. Find the derivative of f(x) = 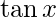\tan x  at x = 0

Solution:

Given: f(x)=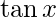\tan x

By using the derivative formula,

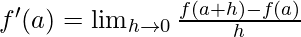f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h {where h is a small positive number}

Derivative of f(x)=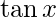\tan x  at x=0 is given as:

f'(0)= \lim_{h \to 0} \frac {f(0+h)-f(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\tan(0+h)-\tan(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\tan(h)-0} h

⇒ f'(0)= \lim_{h \to 0} \frac {\tan(h)} h

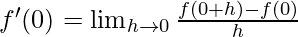
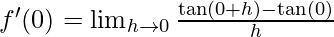
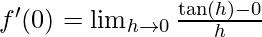
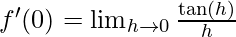
∴ Use the formula: 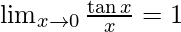 \lim_{x \to 0} \frac {\tan x} x=1  {sandwich theorem}

⇒ f'(0)=1

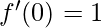
Hence, derivative of f(x)=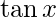\tan x  at x=0 is 1

Question 7(i). Find the derivatives of the following functions at the indicated points : 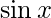\sin x  at x=\pi/2

Solution:

Given: f(x)= 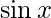\sin x

By using the derivative formula,

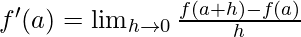f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h {where h is a small positive number}

Derivative of f(x)=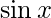\sin x  at x=\pi/2  is given as:

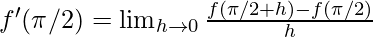
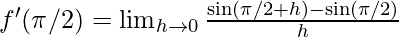
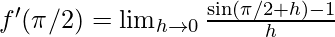
f'(\pi/2)= 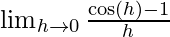\lim_{h \to 0} \frac {f(\pi/2+h)-f(\pi/2)} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {\sin(\pi/2+h)-\sin(\pi/2)} h

⇒  f'(\pi/2)= \lim_{h \to 0} \frac {\sin(\pi/2+h)-1} h

⇒  f'(\pi/2)= \lim_{h \to 0} \frac {\cos(h)-1} h   {∵\sin(\pi/2+x)=\cos x

∵ we can not find the limit of the above function by direct substitution as it gives 0/0 form (indeterminate form)

So we will simplify it to find the limit.

As we know that

1 - \cos x = 2 \sin^2(x/2)

∴ f'(\pi/2)= \lim_{h \to 0} \frac {-(1-\cos(h))} h = - \lim_{h \to 0} \frac {2\sin^2(h/2)} h

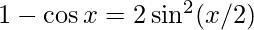
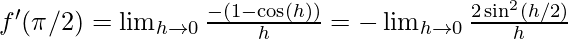
Divide the numerator and denominator by 2 to get the form (sin x)/x for applying sandwich theorem and multiplying h in numerator and denominator to get the required form.

⇒ f'(\pi/2)= -\lim_{h \to 0}( \frac {\frac {2\sin^2(h/2)}2} {\frac {h^2}2}) \times h

⇒ f'(\pi/2)= -\lim_{h \to 0}( \frac {\sin(h/2)} {\frac {h}2}) \times \lim_{h \to 0}h

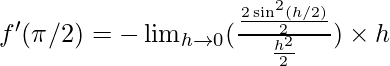
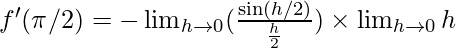
Using the formula:

\lim_{x \to 0} \frac{\sin x}x=1

∴ f'(\pi/2)=-1 \times 0=0

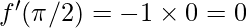
Hence, derivative of f(x)= \sin x  at x=\pi/2  is 0

Question 7(ii). Find the derivatives of the following functions at the indicated points : x at x=1

Solution:

Given: f(x)=x

By using the derivative formula,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {where h is a small positive number}

Derivative of f(x)=x at x=1 is given as:

f'(1)= \lim_{h \to 0} \frac {f(1+h)-f(1)} h

⇒ f'(1)= \lim_{h \to 0} \frac {(1+h)-1} h

⇒ f'(1)= \lim_{h \to 0} \frac {h} h

⇒ f'(1)= \lim_{h \to 0} 1 = 1

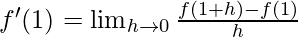
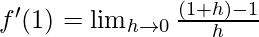
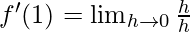
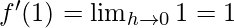
Hence, derivative of f(x)=x at x=1 is 1

Question 7(iii). Find the derivatives of the following functions at the indicated points : 2\cos x at x=\pi/2

Solution:

Given: f(x)= 2\cos x

By using the derivative formula,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {where h is a small positive number}

Derivative of f(x)= 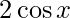2\cos x  at x=\pi/2  is given as:

f'(\pi/2)= \lim_{h \to 0} \frac {f(\pi/2+h)-f(\pi/2)} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {2\cos(\pi/2+h)-2cos(\pi/2)} h

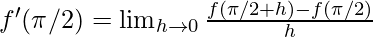
⇒ f'(\pi/2)= \lim_{h \to 0} \frac {-2\sin(h)} h {∵ 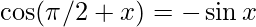\cos(\pi/2+x)=-\sin x }

∵ we can not find the limit of the above function by direct substitution as it gives 0/0 form (indeterminate form)

∴  f'(\pi/2)= -2\lim_{h \to 0} \frac {\sin h} h

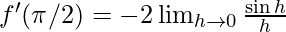
Using the formula: 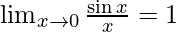 \lim_{x \to 0} \frac{\sin x}x=1

∴ f'(\pi/2)=-2 \times 1=-2

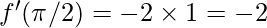
Hence, derivative of f(x)= 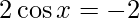2\cos x =-2

Question 7(iv). Find the derivatives of the following functions at the indicated points : 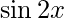\sin 2x  at x=\pi/2

Solution:

Given: f(x)= 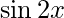\sin 2x

By using the derivative formula,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {where h is a small positive number}

Derivative of f(x)= 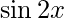\sin 2x  at x=\pi/2  is given as:

f'(\pi/2)= \lim_{h \to 0} \frac {f(\pi/2+h)-f(\pi/2)} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {\sin 2(\pi/2+h)-sin 2(\pi/2)} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {\sin(\pi+2h) - \sin \pi} h  {∵\sin(\pi+x)=-sinx }

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {-\sin(2h) - 0} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {-\sin(2h)} h

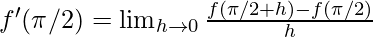
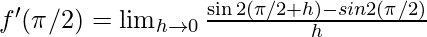
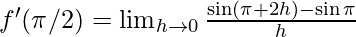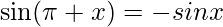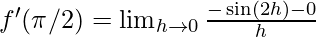
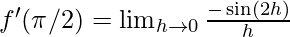
∵ we can not find the limit of the above function by direct substitution as it gives 0/0 form (indeterminate form)

Using the sandwich theorem  and multiplying 2 in numerator and denominator to apply the formula.

f'(\pi/2)= -\lim_{h \to 0} \frac {\sin(2h)} {2h} \times 2 = -2\lim_{h \to 0} \frac {\sin(2h)} {2h}

Using the formula: \lim_{x \to 0} \frac{\sin x}x=1

∴ f'(\pi/2)=-2 \times 1=-2

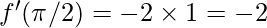
Hence, derivative of f(x)=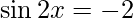\sin 2x=-2  


My Personal Notes arrow_drop_up
Last Updated : 03 Jan, 2021
Like Article
Save Article
Similar Reads
1. Class 11 RD Sharma Solutions - Chapter 31 Derivatives - Exercise 31.1
2. Class 12 RD Sharma Solutions - Chapter 12 Higher Order Derivatives - Exercise 12.1 | Set 1
3. Class 11 RD Sharma Solutions - Chapter 31 Derivatives - Exercise 31.4
4. Class 11 RD Sharma Solutions - Chapter 31 Derivatives - Exercise 31.3
5. Class 11 RD Sharma Solutions - Chapter 31 Derivatives - Exercise 31.2
6. Class 11 RD Sharma Solutions - Chapter 31 Derivatives - Exercise 31.5
7. Class 11 RD Sharma Solutions - Chapter 31 Derivatives - Exercise 31.6
8. Class 11 RD Sharma Solutions - Chapter 30 Derivatives - Exercise 30.2 | Set 1
9. Class 12 RD Sharma Solutions - Chapter 12 Higher Order Derivatives - Exercise 12.1 | Set 2
10. Class 11 RD Sharma Solutions - Chapter 30 Derivatives - Exercise 30.2 | Set 2
Related Tutorials
1. Linear Algebra
2. Maths
3. Physics
4. Chemistry
5. CBSE Class 12 Syllabus 2023-2024
Previous
Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.11
Next
Class 11 RD Sharma Solutions - Chapter 30 Derivatives - Exercise 30.2 | Set 1
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
manandeep1610
manandeep1610
Vote for difficulty
Article Tags :
Report Issue
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox