Question 1. Find f + g, f – g, cf (c ∈ R, c ≠ 0), fg, 1/f and f/g in each of the following:
(i) f(x) = x3 + 1 and g (x) = x + 1
Solution:
Given, f(x) = x3 + 1 and g(x) = x + 1 and f(x): R → R and g(x): R → R
We know, (f + g)(x) = f(x) + g(x) ⇒ (f + g) (x) = x3 + 1 + x + 1 = x3 + x + 2
So, (f + g)(x) = x3 + x + 2
As, (f – g)(x) = f(x) – g(x) ⇒ (f – g)(x) = x3 + 1 – (x + 1) = x3 + 1 – x – 1 = x3 –x
So, (f – g)(x) = x3 – x
Also, (cf)(x) = c × f(x) ⇒ (cf)(x) = c(x3 + 1) = cx3 + c
So, (cf)(x) = cx3 + c
Since, (fg)(x) = f(x)g(x) ⇒ (fg)(x) = (x3 + 1)(x + 1) = (x + 1) (x2 – x + 1) (x + 1) = (x + 1)2 (x2 – x + 1)
So, (fg)(x) = (x + 1)2(x2 – x + 1)
Now, (1/f)(x) = 1/f (x) ⇒ 1/f (x) = 1/(x3 + 1)
Since 1/f(x) is undefined when f(x) = 0 or when x = – 1,
Hence, 1/f: R – {–1} → R is given by 1/f (x) = 1 / (x3 + 1)
Lastly, (f/g)(x) = f(x)/g(x) ⇒ (f/g) (x) = (x3 + 1)/(x + 1)
Since (x3 + 1)/(x + 1) is undefined when g(x) = 0 or when x = –1.
As x3 + 1 = (x + 1)(x2 – x + 1), we have (f/g)(x) = 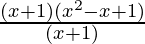 = x2 – x + 1
= x2 – x + 1
Hence, f/g: R – {–1} → R is given by (f/g)(x) = x2 – x + 1
(ii) f(x) = 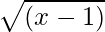 and g(x) =
and g(x) = 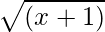
Solution:
Since real square root is defined only for non-negative numbers, f(x): [1, ∞) → R+ and g(x): [–1, ∞) → R+
We know, (f + g)(x) = f(x) + g(x) = 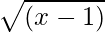 +
+ 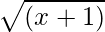
Domain of (f + g) = Domain of f ∩ Domain of g = [1, ∞) ∩ [–1, ∞) = [1, ∞)
Hence, f + g: [1, ∞) → R is given by (f + g)(x) = 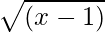 +
+ 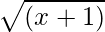
As, (f – g)(x) = f(x) – g(x) = 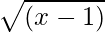 –
– 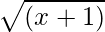
Domain of (f – g) = Domain of f ∩ Domain of g = [1, ∞) ∩ [–1, ∞) = [1, ∞)
Hence, f – g: [1, ∞) → R is given by (f – g)(x) = 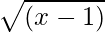 –
– 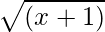
Since, (cf)(x) = c × f(x) = c 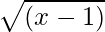
Domain of (cf) = Domain of f = [1, ∞)
Hence, cf: [1, ∞) → R is given by (cf)(x) = c 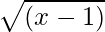
Also, (fg)(x) = f(x)g(x) = 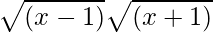 =
= 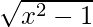
Domain of (fg) = Domain of f ∩ Domain of g = [1, ∞) ∩ [–1, ∞) = [1, ∞)
Hence, fg: [1, ∞) → R is given by (fg)(x) = 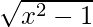
Now, (1/f) (x) = 1/f(x) = 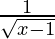
Domain of (1/f) = Domain of f = [1, ∞)
Since 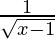 is also undefined when x – 1 = 0 or x = 1.
is also undefined when x – 1 = 0 or x = 1.
Hence, 1/f: (1, ∞) → R is given by (1/f)(x) = 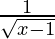
Lastly, (f/g) (x) = f(x)/g(x) =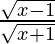
Domain of (f/g) = Domain of f ∩ Domain of g = [1, ∞) ∩ [–1, ∞) = [1, ∞)
Hence, f/g: [1, ∞) → R is given by (f/g) (x) =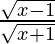
Question 2. Let f(x) = 2x + 5 and g(x) = x2 + x. Describe and find domain in each:
(i) f + g
Solution:
Given, f(x) = 2x + 5 and g(x) = x2 + x
Both f(x) and g(x) are defined for all x ∈ R.
So, domain of f = domain of g = R
We know, (f + g)(x) = f(x) + g(x) ⇒ (f + g)(x) = 2x + 5 + x2 + x
= x2 + 3x + 5
Since (f + g)(x) Is defined for all real numbers x.
Hence, (f + g)(x) = x2 + 3x + 5 and the domain of (f + g) is R.
(ii) f – g
Solution:
As (f – g)(x) = f(x) – g(x) ⇒ (f – g)(x)
= 2x + 5 – (x2 + x)
= 2x + 5 – x2 – x
= 5 + x – x2
Since (f – g)(x) is defined for all real numbers x.
Hence, (f – g)(x) = 5 + x – x2 and the domain of (f – g) is R.
(iii) fg
Solution:
We know, (fg)(x) = f(x)g(x) ⇒ (fg)(x) = (2x + 5)(x2 + x)
= 2x(x2 + x) + 5(x2 + x)
= 2x3 + 2x2 + 5x2 + 5x
= 2x3 + 7x2 + 5x
Since (fg)(x) is defined for all real numbers x.
Hence, (fg)(x) = 2x3 + 7x2 + 5x and the domain of fg is R.
(iv) f/g
Solution:
We know, (f/g) (x) = f(x)/g(x) ⇒ (f/g)(x) = 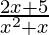
Clearly (f/g)(x) is defined for all real values of x, except for the case when x2 + x = 0.
x2 + x = 0 ⇒ x(x + 1) = 0 ⇒ x = 0 or x + 1 = 0 ⇒ x = 0 or –1
When x = 0 or –1, (f/g)(x) will be undefined.
Hence, The domain of f/g = R – {–1, 0}
Question 3. If f(x) be defined on [–2, 2] and is given by 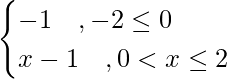 and g(x) = f(|x|) + |f(x)|. Find g(x).
and g(x) = f(|x|) + |f(x)|. Find g(x).
Solution:
f(|x|) = |x| – 1, where –2 ≤ x ≤ 2
and, |f(x)| = 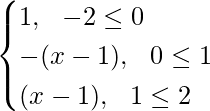
Thus, g(x) = f(|x|) + |f(x)| = 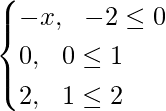
Question 4. Let f, g be two real functions defined by f(x) = 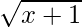 and g(x) =
and g(x) = 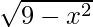 . Then, describe each of the following functions.
. Then, describe each of the following functions.
(i) f + g
Solution:
Given, f(x) = 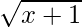 and g(x) =
and g(x) = 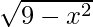
f(x) takes real values only when x + 1 ≥ 0 x ≥ –1, x ∈ [–1, ∞) ⇒ Domain of f = [–1, ∞)
g(x) takes real values only when 9 – x2 ≥ 0
⇒ x2 ≤ 9 ⇒ x2 – 32 ≤ 0 ⇒ (x + 3)(x – 3) ≤ 0
⇒ x ≥ –3 and x ≤ 3
⇒ Domain of g = [–3, 3]
We know, (f + g)(x) = f(x) + g(x) ⇒ (f + g) (x) = 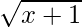 +
+ 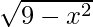
Domain of f + g = Domain of f ∩ Domain of g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
Hence, f + g: [–1, 3] → R is given by (f + g)(x) = f(x) + g(x) = 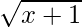 +
+ 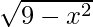
(ii) g – f
Solution:
We know, (g – f)(x) = g(x) – f(x) ⇒ (g – f)(x) =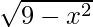 –
– 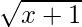
Domain of g – f = Domain of g ∩ Domain of f = [–3, 3] ∩ [–1, ∞) = [–1, 3]
Hence, g – f: [–1, 3] → R is given by (g – f) (x) = g(x) – f(x) = 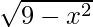 –
– 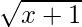
(iii) fg
Solution:
We know, (fg)(x) = f(x)g(x) ⇒ (fg)(x) = 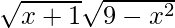
= 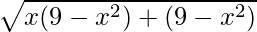
= 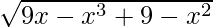
= 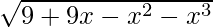
Domain of fg = Domain of f ∩ Domain of g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
Hence, fg: [–1, 3] → R is given by (fg) (x) = f(x) g(x) = 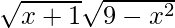 =
= 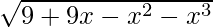
(iv) f/g
Solution:
We know, (f/g) (x) = f(x)/g(x) ⇒ (f/g) (x) = 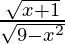
Domain of f/g = Domain of f ∩ Domain of g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
However, (f/g) (x) is defined for all real values of x ∈ [–1, 3], except for the case when 9 – x2 = 0 or x = ± 3
When x = ±3, (f/g) (x) will be undefined as the division result will be indeterminate.
Domain of f/g = [–1, 3] – {–3, 3} = [–1, 3)
Hence, f/g: [–1, 3) → R is given by (f/g) (x) = f(x)/g(x) = 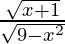
(v) g/f
Solution:
We know, (g/f)(x) = g(x)/f(x) ⇒ (g/f)(x) = 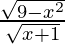
Domain of g/f = Domain of f ∩ Domain of g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
However, (g/f) (x) is defined for all real values of x ∈ [–1, 3], except for the case when x + 1 = 0 or x = –1
When x = –1, (g/f) (x) will be undefined as the division result will be indeterminate.
Domain of g/f = [–1, 3] – {–1} = (–1, 3]
Hence, g/f: (–1, 3] → R is given by (g/f) (x) = g(x)/f(x) =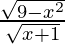
(vi) 2f – √5 g
Solution:
We know, (2f – √5g)(x) = 2f(x) – √5g(x)
⇒ (2f – √5g)(x) = 2f (x) – √5g(x)
= 2 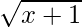 –
– 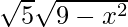
= 2 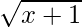 –
– 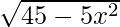
Domain of 2f – √5g = Domain of f ∩ Domain of g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
Hence, 2f – √5g: [–1, 3] → R is given by (2f – √5g) (x) = 2f(x) – √5 g(x) = 2 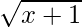 –
– 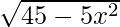
(vii) f2 + 7f
Solution:
We know, (f2 + 7f)(x) = f2(x) + (7f)(x)
⇒ (f2 + 7f) (x) = f(x).f(x) + 7f(x)
=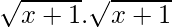 + 7
+ 7 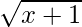
= x + 1 + 7 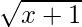
Domain of f2 + 7f is same as domain of f = [–1, ∞)
Hence, f2 + 7f: [–1, ∞) → R is given by (f2 + 7f) (x) = f(x) f(x) + 7f(x) = x + 1 + 7 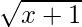
(viii) 5/g
Solution:
We know, (5/g)(x) = 5/g(x) ⇒ (5/g)(x) = 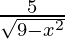
Domain of 5/g = Domain of g = [–3, 3]
However, (5/g)(x) is defined for all real values of x ∈ [–3, 3], except for the case when 9 – x2 = 0 or x = ± 3
When x = ±3, (5/g)(x) will be undefined.
Thus, Domain of 5/g = [–3, 3] – {–3, 3} = (–3, 3)
Hence, 5/g: (–3, 3) → R is given by (5/g)(x) = 5/g(x) = 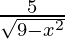
Question 5. If f(x) = loge (1 – x) and g(x) = [x], then determine each of the following functions:
(i) f + g
Solution:
f(x) = loge (1 – x) and g(x) = [x]
We know, f(x) takes real values only when 1 – x > 0 or when 1 > x
x < 1, ∴ x ∈ (–∞, 1) ⇒ Domain of f = (–∞, 1)
g(x) is defined for all real numbers x. ⇒ Domain of g = [x], x ∈ R = R
Thus, (f + g)(x) = f(x) + g(x) = loge(1 – x) + [x]
Domain of f + g = Domain of f ∩ Domain of g = (–∞, 1) ∩ R = (–∞, 1)
Hence, f + g: (–∞, 1) → R is given by (f + g) (x) = loge(1 – x) + [x]
(ii) fg
Solution:
We know, (fg)(x) = f(x)g(x) ⇒ (fg)(x) = loge(1 – x) × [x] = [x]loge(1 – x)
Domain of fg = Domain of f ∩ Domain of g = (–∞, 1) ∩ R = (–∞, 1)
Hence, fg: (–∞, 1) → R is given by (fg) (x) = [x] loge(1 – x).
(iii) f/g
Solution:
We know, (f/g)(x) = f(x)/g(x) ⇒ (f/g)(x) = 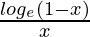
Domain of f/g = Domain of f ∩ Domain of g = (–∞, 1) ∩ R = (–∞, 1)
However, (f/g) (x) is defined for all real values of x ∈ (–∞, 1), except when [x] = 0.
We have, [x] = 0 when 0 ≤ x < 1 or x ∈ [0, 1)
When 0 ≤ x < 1, (f/g) (x) will be undefined. Domain of f/g = (–∞, 1) – [0, 1) = (–∞, 0)
Hence, f/g: (–∞, 0) → R is given by (f/g)(x) =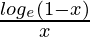
(iv) g/f
Solution:
We know, (g/f)(x) = g(x)/f(x) ⇒ (g/f)(x) = 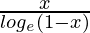
However, (g/f)(x) is defined for all real values of x ∈ (–∞, 1), except for the case when loge (1 – x) = 0.
⇒ loge (1 – x) = 0 ⇒ 1 – x = 1
or x = 0
When x = 0, (g/f) (x) will be undefined as the division result will be indeterminate.
Domain of g/f = (–∞, 1) – {0} = (–∞, 0) ∪ (0, 1)
Hence, g/f: (–∞, 0) ∪ (0, 1) → R is given by (g/f)(x) = 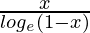
(v) (f + g)(–1)
Solution:
(f + g) (x) = loge(1 – x) + [x], x ∈ (–∞, 1)
Substituting x = –1 in the above equation, we get
(f + g)(–1) = loge(1 – (–1)) + [–1]
= loge(1 + 1) + (–1)
= loge2 – 1
Hence, (f + g)(–1) = loge2 – 1
(vi) (fg)(0)
Solution:
We have, (fg)(x) = [x]loge(1 – x), x ∈ (–∞, 1)
Substituting x = 0 in the above equation, we get
(fg)(0) = [0]loge(1 – 0)
= 0 × loge1 = 0
Hence, (fg) (0) = 0
(vii) (f/g)(1/2)
Solution:
(f/g)(x) = 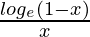 , x ∈ (–∞, 0)
, x ∈ (–∞, 0)
However, 1/2 is not in the domain of f/g.
Hence, (f/g)(1/2) does not exist.
(viii) (g/f)(1/2)
Solution:
We have, (g/f)(x) =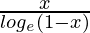 , x ∈ (–∞, 0) ∪ (0, ∞)
, x ∈ (–∞, 0) ∪ (0, ∞)
Substituting x=1/2 in the above equation, we get
(g/f)(1/2) = 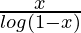
= 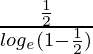
= 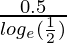
=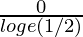 = 0
= 0
Hence, (g/f)(1/2) = 0
Question 6. If f, g, h are real functions defined by f(x) = 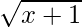 , g(x) = 1/x and h(x) = 2x2 – 3, then find the values of (2f + g – h)(1) and (2f + g – h)(0).
, g(x) = 1/x and h(x) = 2x2 – 3, then find the values of (2f + g – h)(1) and (2f + g – h)(0).
Solution:
Since, f(x) is defined for x + 1 ≥ 0 ⇒ x ≥ – 1
⇒ x ∈ [– 1, ∞] = Domain of f(x)
Now, (2f+g –h)(x) = 2f(x) + g(x) – h(x)
= 2 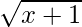 + 1/x – (2x2 – 3)
+ 1/x – (2x2 – 3)
= 2 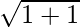 + 1/1 – 2(1)2 + 3
+ 1/1 – 2(1)2 + 3
(2f + g – h)(x) = 2√2 + 2
Since (2f+g –h)(0) does not lie in the domain x ∈ [– 1, ∞] – 0, it does not exist.
Question 7. The function f(x) is defined by: f(x) = 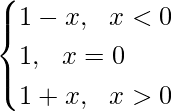 . Draw the graph of f(x).
. Draw the graph of f(x).
Solution:
The graph of f(x) for x < 0 lies to the left of origin.
The graph of f(x) for x > 0 lies to the right of origin.
The graph of f(x) for x = 0 is represented by the point (0,1).

Question 8. Let f, g: R ⇒ R be defined respectively as f(x) = x + 1 and g(x) = 2x – 3. Find f + g, f – g and f/g.
Solution:
We know, (f + g)(x) = f(x) + g(x) = (x + 1 + 2x – 3) = 3x – 2.
Now, (f – g)(x) = f(x) – g(x) = (x + 1) – (2x – 3) = 4 – x.
f/g(x) = f(x)/g(x) = 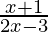
Question 9. Let f and g be defined respectively as f(x) = √x and g(x) = x. Find f + g, f – g, fg, and f/g.
Solution:
(f + g)(x) = f(x) + g(x) = √x + x
(f – g)(x) = f(x) – g(x) = √x – x
(fg)(x) = f(x)g(x) = √x.x = x1/2 + 1 = x3/2
f/g(x) = f(x)/g(x) = √x/x = 1/√x
Question 10. Let f(x) = x2 and g(x) = 2x + 1 be two real functions. Find f + g, f – g, fg, and f/g.
Solution:
(f + g)(x) = f(x) + g(x) = x2 + 2x + 1 = (x + 1)2
(f – g)(x) = f(x) – g(x) = x2 – 2x – 1
(fg)(x) = f(x)g(x) = x2(2x + 1) = 2x3 + x2
f/g(x) = f(x)/g(x) = 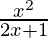
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...