Class 11 RD Sharma Solutions – Chapter 3 Functions – Exercise 3.2
Last Updated :
25 Jan, 2021
Question 1. If f(x)=x2-3x+4, then find the values of x satisfying the equation f(x)=f(2x+1).
Solution:
We have,
f(x)=x2-3x+4
Now,
f(2x+1)=(2x+1)2-3(2x+1)+4
f(2x+1)=4x2+1+4x-6x-3+4
f(2x+1)=4x2-2x+2
It is given that
f(x)=f(2x+1)
x2-3x+4=4x2-2x+2
0=4x2-x2-2x+3x+2-4
3x2+x-2=0
3x2+3x-2x-2=0
3x(x+1)-2(x+1)=0
(x+1)(3x-2)=0
x+1=0 or 3x-2=0
x=-1 or x=2/3
Therefore, the value of x are -1 and 2/3.
Question 2. If f(x)=(x-a)2 (x-b)2 ,find f(a+b).
Solution:
We have,
f(x)=(x-a)2(x-b)2
Now, let us find f(a+b)
f(a+b)=(a+b-a)2(a+b-b)2
f(a+b)=b2a2
Therefore, f(a+b)=(ba)2
Question 3. If y=f(x)=(ax-b)/(bx-a), show that x=f(y).
Solution:
Given,
y=f(x)=(ax-b)/(bx-a)
As we know, f(y)=(ay-b)/(by-a)
Let us prove that x=f(y).
We have,
y=(ax-b)/(bx-a)
By cross multiplying,
y(bx-a)=ax-b
bxy-ay=ax-b
bxy-ax=ay-b
x(by-a)=ay-b
x=(ay-b)/(by-a)
Therefore, x=f(y)
Hence proved.
Question 4. If f (x) = 1 / (1 – x), show that f [f {f (x)}] = x.
Solution:
Given:
f (x) = 1 / (1 – x)
Let us prove that f [f {f (x)}] = x.
Firstly, let us solve for f {f (x)}.
f {f (x)} = f {1/(1 – x)}
= 1 / 1 – (1/(1 – x))
= 1 / [(1 – x – 1)/(1 – x)]
= 1 / (-x/(1 – x))
= (1 – x) / -x
= (x – 1) / x
∴ f {f (x)} = (x – 1) / x
Now, we shall solve for f [f {f (x)}]
f [f {f (x)}] = f [(x-1)/x]
= 1 / [1 – (x-1)/x]
= 1 / [(x – (x-1))/x]
= 1 / [(x – x + 1)/x]
= 1 / (1/x)
∴ f [f {f (x)}] = x
Hence proved.
Question 5. If f (x) = (x + 1) / (x – 1), show that f [f (x)] = x.
Solution:
Given:
f (x) = (x + 1) / (x – 1)
We have to prove that f [f (x)] = x.
f [f (x)] = f [(x+1)/(x-1)]
= [(x+1)/(x-1) + 1] / [(x+1)/(x-1) – 1]
= [[(x+1) + (x-1)]/(x-1)] / [[(x+1) – (x-1)]/(x-1)]
= [(x+1) + (x-1)] / [(x+1) – (x-1)]
= (x+1+x-1)/(x+1-x+1)
= 2x/2
= x
∴ f [f (x)] = x
Hence proved.
Question 6. If
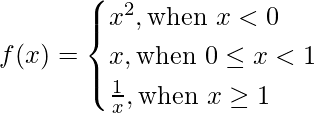
Find:
(i) f (1/2)
(ii) f (-2)
(iii) f (1)
(iv) f (√3)
(v) f (√-3)
Solution:
(i) f (1/2)
When, 0 ≤ x ≤ 1, f(x) = x
∴ f (1/2) = 1/2
(ii) f (-2)
When, x < 0, f(x) = x2
f (–2) = (–2)2
= 4
∴ f (–2) = 4
(iii) f (1)
When, x ≥ 1, f (x) = 1/x
f (1) = 1/1
∴ f(1) = 1
(iv) f (√3)
We have √3 = 1.732 > 1
When, x ≥ 1, f (x) = 1/x
∴ f (√3) = 1/√3
(v) f (√-3)
We know √-3 is not a real number and the function f(x) is defined only when x ∈ R.
∴ f (√-3) does not exist.
Question 7. If f(x)=x3-(1/x3), show that f(x)+f(1/x)=0.
Solution:
We have,
f(x)=x3-(1/x)3 —(i)
Now,
f(1/x)=(1/x)3-(1/(1/x)3)
f(1/x)=(1/x)3-x3 —(ii)
Adding equation (i) and (ii), we get
f(x)+f(1/x) = (x3-1/x3)+(1/x3-x3)
f(x)+f(1/x)=x3-x3+1/x3-1/x3
f(x)+f(1/x)=0
Hence, proved.
Question 8. If f(x)= 2x/(1+x2),show that f(tan θ)=sin 2θ.
Solution.
We have,
f(x)=2x/(1+x2)
Now,
f(tan θ)=2(tan θ)/(1+tan2 θ)
f(tan θ)=sin 2θ (Because, sin 2θ = 2(tan θ)/(1+tan2θ))
Hence, proved.
Question 9. If f(x)=(x-1)/(x+1), then show that
i) f(1/x)=-f(x)
ii) f(1/(-x))=-1/f(x)
Solution.
i) We have,
f(x)=(x-1)/(x+1)
Now,
f(1/x)=((1/x)-1)/((1/x)+1)
f(1/x)=((1-x)/x)/((1+x)/x)
f(1/x)=(1-x)/(1+x)=f(-x)
Hence, proved.
ii) We have,
f(x)=(x-1)/(x+1)
Now,
f(1/(-x))= ((1/(-x))-1)/((1/(-x))+1)
f(1/(-x))=((1+x)/(-x))/((1-x)/(-x))
f(1/(-x))=(1+x)/(1-x)
f(1/(-x))=(-1)/((x-1)/(x+1))
f(1/(-x))=-1/f(x)
Hence, proved.
Question 10. If f(x)=(a-xn)1/n ,a>0 and n ∈ N, then prove that f(f(x))=x for all x.
Solution.
We have,
![Rendered by QuickLaTeX.com f(x)=(a-x^n)^\frac{1}{n}, a>0\\ \newline \\ Now, \\ f(f(x))=f(a-x^n)^\frac{1}{n}\\ f(f(x))=[a-\{(a-x^n)^\frac{1}{n}\}^n]^\frac{1}{n} \\ f(f(x))=[a-(a-x^n)]^\frac{1}{n}\\ f(f(x))=[a-a+x^n]^\frac{1}{n}\\ f(f(x))=(x^n)^\frac{1}{n}\\ f(f(x))=x\\ Hence, proved](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cbf49f4813d2ad7666611839655398e7_l3.png)
Question 11. If for non-zero x, a f(x)+b f(1/x) = 1/x – 5, where a ≠ b, then find f(x).
Solution.
We have,
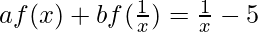 —(i)
—(i)
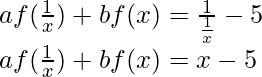
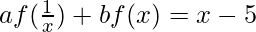 —(ii)
—(ii)
Adding equation (i) and (ii), we get
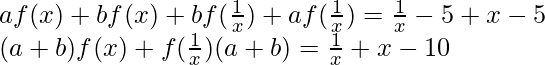
![Rendered by QuickLaTeX.com f(x)+f(\frac{1}{x})=\frac{1}{a+b}[\frac{1}{x}+x-10]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-63d2cab94c972f1cf136b75d47a2ec67_l3.png) —(iii)
—(iii)
Subtracting equation (ii) from equation (i)
![Rendered by QuickLaTeX.com af(x)-bf(x )+bf(\frac{1}{x})-af(\frac{1}{x})=\frac{1}{x}-5-x+5 \\ (a-b)f(x)-f(\frac{1}{x})(a-b)=\frac{1}{x}-x \\ f(x)-f(\frac{1}{x})=\frac{1}{a-b}[\frac{1}{x}-x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a751155103c5a647b28e25650b0d1373_l3.png) —(iv)
—(iv)
Adding equations(iii) and (iv), we get
![Rendered by QuickLaTeX.com 2f(x)=\frac{1}{a+b}[\frac{1}{x}+x-10]+\frac{1}{a-b}[\frac{1}{x}-x]\\ 2f(x)=\frac{(a-b)[\frac{1}{x}+x-10]+(a+b)[\frac{1}{x}-x]}{(a+b)(a-b)} \\ 2f(x)=\frac{\frac{a}{x}+ax-10a-\frac{b}{x}-bx+10b+\frac{a}{x}-ax+\frac{b}{x}-bx}{a^2-b^2} \\ 2f(x)=\frac{\frac{2a}{x}-10a+10b-2bx}{a^2-b^2} \\ f(x)=\frac{1}{a^2-b^2}\times\frac{1}{2}[\frac{2a}{x}-10a+10b-2bx]\\ f(x)=\frac{1}{a^2-b^2}[\frac{a}{x}-5a+5b-bx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a7fa75719fb7844e97a763b99a4b66e_l3.png)
Therefore,
![Rendered by QuickLaTeX.com f(x)=\frac{1}{a^2-b^2}[\frac{a}{x}-5a+5b-bx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d95002e95d4a98a994303888d59db8c_l3.png)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...