Class 11 RD Sharma Solutions – Chapter 29 Limits – Exercise 29.8 | Set 2
Last Updated :
08 May, 2021
Question 20. limx→1[(1 + cosπx)/(1 – x)2]
Solution:
We have,
limx→1[(1 + cosπx)/(1 – x)2]
Here, x→1, h→0
= Limh→0[{1 + cosπ(1 + h)}/{1 – (1 + h)}2]
= Limh→0[(1 – cosπh)/h2]
= Limh→0[2sin2(πh/2)/h2]
= ![Rendered by QuickLaTeX.com 2\lim_{h\to0}[\frac{sin^2(\frac{πh}{2})}{(\frac{2}{π})^2×(\frac{πh}{2})^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3661205844e7de55434ae913bc99ddbe_l3.png)
= 2π2/4
= π2/2
Question 21. limx→1[(1 – x2)/sinπx]
Solution:
We have,
limx→1[(1 – x2)/sinπx]
Here, x→1, h→0
= limh→0[{1 – (1 – h)2}/sinπ(1 – h)]
= limh→0[(2h – h2)/-sinπh]
= -limh→0[{h(2 – h)}/sinπh]
=![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{(2-h)}{\frac{sinπh}{h}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bccd2e6805be883ef261a3191dedae45_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{(2-h)}{(\frac{sinπh}{πh})×π}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-02f145477f53890c89dfbfb58d1e1bb6_l3.png)
= (2 – 0)/π
= 2/π
Question 22. limx→π/4[(1 – sin2x)/(1 + cos4x)]
Solution:
We have,
limx→π/4[(1 – sin2x)/(1 + cos4x)]
Here, x→π/4, h→0
= limh→0[{1 – sin2(π/4 – h)}/{1 + cos4(π/4 – h)}]
= limh→0[{1 – sin(π/2 – 2h)}/{1 + cos(π – 4h)}]
= limh→0[(1 – cos2h)/(1 – cos4h)]
= limh→0[2sin2h/2sin22h]
=![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{\frac{sin^2h}{h^2}}{\frac{sin^22h}{4h^2}×4}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69baa94f2fa56f53968db44cb164289b_l3.png)
= (1/4)
Question 23. limx→π[(1 + cosx)/tan2x]
Solution:
We have,
limx→π[(1 + cosx)/tan2x]
Here, x→π, h→0
= limh→0[{1+cos(π + h)}/tan2(π + h)]
= limh→0[(1 – cosh)/tan2h]
= limh→0[{2sin2(h/2)}/tan2h]
= ![Rendered by QuickLaTeX.com 2×\lim_{h\to0}[\frac{sin^2(\frac{h}{2})}{(\frac{h}{2})^2×(\frac{2}{h})^2}]×\lim_{h\to0}[\frac{1}{\frac{tan^2h}{h^2}×h^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-27483a2b55268d5c7188abc55b7e0fd1_l3.png)
= 2/4
= 1/2
Question 24. limn→∞[nsin(π/4n)cos(π/4n)]
Solution:
We have,
limn→∞[nsin(π/4n)cos(π/4n)]
= limn→∞[nsin(π/4n)]Limn→∞[cos(π/4n)]
=![Rendered by QuickLaTeX.com \lim_{n\to∞}[\frac{nsin\frac{π}{4n}}{(\frac{π}{4n})}]×(\frac{π}{4n})×1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d83eb9c91a800de6a5f42dc5b0cc4040_l3.png)
=![Rendered by QuickLaTeX.com (\frac{π}{4})\lim_{n\to∞}[\frac{sin\frac{π}{4n}}{(\frac{π}{4n})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa52860ff621691eeba0a00f7df663f4_l3.png)
Let, y = (π/4n)
If n→∞, y→0.
= (π/4).Limy→0[siny/y]
= (π/4)
Question 25. limn→∞[2n-1sin(a/2n)]
Solution:
We have,
limn→∞[2n-1sin(a/2n)]
=![Rendered by QuickLaTeX.com \lim_{n\to∞}[\frac{2^n}{2}×sin(\frac{a}{2^n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f44b4bb23f836a69d7437c1b7a09469f_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to∞}[\frac{2^n}{2}×\frac{sin(\frac{a}{2^n})}{\frac{a}{2^n}}×\frac{a}{2^n}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72dfeaa93ee0fe9a32e5e00973c0e2ad_l3.png)
=![Rendered by QuickLaTeX.com (\frac{a}{2})\lim_{n\to∞}[\frac{sin\frac{a}{2^n}}{(\frac{a}{2^n})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fd8d44bcf8d525138710433b2d29ef47_l3.png)
Let, y = (a/2n)
If n→∞, y→0
= (a/2).Limy→0[siny/y]
= (a/2)
Question 26. limn→∞[sin(a/2n)/sin(b/2n)]
Solution:
We have,
limn→∞[sin(a/2n)/sin(b/2n)]
=![Rendered by QuickLaTeX.com \lim_{n\to∞}[\frac{sin(\frac{a}{2^n})}{(\frac{a}{2^n})}×(\frac{a}{2^n})]\lim_{n\to∞}[\frac{}{\frac{sin(\frac{b}{2^n})}{(\frac{b}{2^n})}×(\frac{b}{2^n})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-afa9585b54576e4c99be357737b34f0f_l3.png)
Let, y = (a/2n) and z = (b/2n)
If n→∞, y→0 and z→0
=![Rendered by QuickLaTeX.com \frac{y}{z}\lim_{y\to0}[\frac{siny}{y}]\lim_{z\to0}[\frac{y}{siny}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3aadaad8a4825f3a0078c616b8c0e9c8_l3.png)
=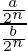
= (a/b)
Question 27. limx→-1[(x2 – x – 2)/{(x2 + x) + sin(x + 1)}]
Solution:
We have,
limx→-1[(x2 – x – 2)/{(x2 + x) + sin(x + 1)}]
= limx→-1[(x2 – x – 2)/{x(x + 1) + sin(x + 1)}]
= limx→-1[(x – 2)(x + 1)/{x(x + 1) + sin(x + 1)}]
Let, y = x + 1
If x→-1, then y→0
= limy→0[y(y – 3)/{y(y – 1) + siny}]
=![Rendered by QuickLaTeX.com \lim_{y\to0}[\frac{(y-3)}{(y-1)+\frac{siny}{y}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cce51120accd78fbf06159c9cfe40bf7_l3.png)
= (0 – 3)/{(0 – 1) + 1}
= -3/0
= ∞
Question 28. limx→2[(x2 – x – 2)/{(x2 – 2x) + sin(x – 2)}]
Solution:
We have,
limx→2[(x2 – x – 2)/{(x2 – 2x) + sin(x – 2)}]
= limx→2[{(x – 2)(x + 1)}/{x(x + 1) + sin(x + 1)}]
Let, y = x – 2
If x→2, then y→0
= limy→0[y(y + 3)/{y(y + 2) + siny}]
= ![Rendered by QuickLaTeX.com \lim_{y\to0}[\frac{(y+3)}{(y+2)+\frac{siny}{y}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e56205cb13100fc52b0fc31b823a3545_l3.png)
= (0 + 3)/{(0 + 1) + 1}
= 3/3
= 1
Question 29. limx→1[(1 – x)tan(πx/2)]
Solution:
We have,
limx→1[(1 – x)tan(πx/2)]
Here, x→1, h→0
= limh→0[{1 – (1 – h)}tan{π/2(1 – h)}]
= limh→0[htan{π/2-πh/2)}
= limh→0[hcot(πh/2)]
=![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{h}{tan(\frac{πh}{2})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3ebf5594d92581ccb24a7ea67317d2a3_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{1}{\frac{tan(\frac{πh}{2})}{\frac{πh}{2}}×\frac{π}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc95870e3b84de207af7faf9a2e48332_l3.png)
=
= (2/π)
Question 30. limx→π/4[(1 – tanx)/(1 – √2sinx)]
Solution:
We have,
limx→π/4[(1 – tanx)/(1 – √2sinx)]
On rationalizing the denominator.
= limx→π/4[{(1 – tanx)(1 – √2sinx)}/(1 – 2sin2x)]
=![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{4}}[\frac{(1-\frac{sinx}{cosx})(1+\sqrt2sinx)}{cos2x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-24932d334519195b4ec92b4a08c09248_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{4}}[\frac{(cosx-sinx)(1+\sqrt2sinx)}{cosx.cos2x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-44827246de7e509dba1390396a350a41_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{4}}[\frac{(cosx-sinx)(1+\sqrt2sinx)}{cosx.(cos^2x-sin^2x)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f8b2e2e4246afc40293b2ec9318603f4_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{4}}[\frac{(cosx-sinx)(1+\sqrt2sinx)}{cosx.(cosx-sinx)(cosx+sinx)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-31d9427c08fe532a117e994f06f955ea_l3.png)
=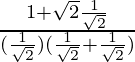
= 2/1
= 2
Question 31. limx→π[{√(2 + cosx) – 1}/(π – x)2]
Solution:
We have,
limx→π[{√(2 + cosx) – 1}/(π – x)2]
Let, y = [π – x]
Here, x→π, y→0
=![Rendered by QuickLaTeX.com \lim_{y\to0}[\frac{\sqrt{2+cos(π-y)}-1}{y^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-926d8778df41d1d331b23513c82b1132_l3.png)
= limy→0[{√(2 – cosy) – 1}/y2]
On rationalizing the numerator, we get
=![Rendered by QuickLaTeX.com \lim_{y\to0}[\frac{2-cosy-1}{y^2(\sqrt{2-cosy}-1)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c7eeecb12738dceef99ad10bf117029c_l3.png)
= limy→0[{1 – cosy}/y2{√(2 – cosy) – 1}]
=![Rendered by QuickLaTeX.com \lim_{y\to0}[\frac{2sin^2\frac{y}{2}}{y^2(\sqrt{2-cosx}+1)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8270f6bd4104aeec99a097c50e80b39c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{y\to0}[\frac{2sin^2\frac{y}{2}}{(\frac{y}{2})^2(\sqrt{2-cosx}+1)×4}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-82fcece0d8d9405ac204c7da549e0b90_l3.png)
= 2 × (1/4) × {1/(1 + 1)}
= (1/4)
Question 32. limx→π/4[(√cosx – √sinx)/(x – π/4)]
Solution:
We have,
limx→π/4[(√cosx – √sinx)/(x – π/4)]
On rationalizing the numerator, we get
= limx→π/4[(cosx – sinx)/{(√cosx + √sinx)(x – π/4)}]
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{cos(\frac{π}{4}+h)-sin(\frac{π}{4}+h)}{(\frac{π}{4}+h-\frac{π}{4})(\sqrt{cos(\frac{π}{4}+h)}+\sqrt{sin(\frac{π}{4}+h)}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-decca72c9b18f81cd85de12bccdf5545_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{-2×\frac{1}{\sqrt2}×sinh}{h(\sqrt{cos(\frac{π}{4}+h)}+\sqrt{sin(\frac{π}{4}+h)})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3709dc226b20600677f503fed0e01e1f_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{-\sqrt2×sinh}{h(\sqrt{cos(\frac{π}{4}+h)}+\sqrt{sin(\frac{π}{4}+h)})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d69507132dd52f396841bd179003472a_l3.png)
=![Rendered by QuickLaTeX.com -\sqrt2[\frac{1}{(\frac{1}{\sqrt2})^{\frac{1}{2}}+(\frac{1}{\sqrt2})^{\frac{1}{2}}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6fb32534ce2a73713a8a605a46d59225_l3.png)
Question 33. limx→1[(1 – 1/x)/sinπ(x – 1)]
Solution:
We have,
limx→1[(1 – 1/x)/sinπ(x – 1)]
= limx→1[(x – 1)/x{sinπ(x – 1)}]
Let, y = x – 1
If x→1, then y→0
= limy→0[y/{(y + 1)sin(πy)}]
= ![Rendered by QuickLaTeX.com \lim_{y\to0}[\frac{1}{\frac{(y+1).sin(πy)}{y}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8a3ef01a9bddf209dc12439feb7fbfd_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{y\to0}[\frac{1}{\frac{(y+1).sin(πy)}{πy}×π}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b3f0ddf66c669599881021fa62b2a810_l3.png)
= 1/{(1 + 0) × 1 × π}
= 1/π
Question 34. limx→π/6[(cot2x – 3)/(cosecx – 2)]
Solution:
We have,
limx→π/6[(cot2x – 3)/(cosecx – 2)]
= limx→π/6[(cosec2x – 1 – 3)/(cosecx – 2)]
= limx→π/6[(cosec2x – 22)/(cosecx – 2)]
= limx→π/6[{(cosecx + 2)(cosecx – 2)}/(cosecx – 2)]
= limx→π/6[(cosecx + 2)]
= cosec(π/6) + 2
= 2 + 2
= 4
Question 35. limx→π/4[(√2 – cosx – sinx)/(4x – π)2]
Solution:
We have,
limx→π/4[(√2 – cosx – sinx)/(4x – π)2]
= limx→π/4[(√2 – cosx – sinx)/{42(π/4 – x)2}]
=![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{2}}\frac{\sqrt2[1-(\frac{1}{\sqrt2}.cosx+\frac{1}{\sqrt2}.sinx)]}{4^2(\frac{π}{4}-x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3ce670266757290fa6de9595e8f27f8e_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{2}}\frac{\sqrt{2}[1-cos(\frac{π}{4}-x)]}{4^2(\frac{π}{4}-x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5f3750173b4065c73be13410f4ae58d2_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{2}}\frac{[2\sqrt{2}sin^2\frac{(\frac{π}{4}-x)}{2}]}{4^2(\frac{π}{4}-x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-77c0efbb74872e9d455f252eb3c127ff_l3.png)
=![Rendered by QuickLaTeX.com 2\sqrt{2}\lim_{x\to \frac{π}{2}}\frac{[sin^2\frac{(\frac{π}{4}-x)}{2}]}{4^2×\frac{(\frac{π}{4}-x)}{4}^2×4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-93de6a9a022e1f7ede84999db1c05916_l3.png)
= 2√2/43
= (2√2 × √2)/(43√2)
= 4/(43√2)
= 1/(16√2)
Question 36. limx→π/2[{(π/2 – x)sinx – 2cosx}/{(π/2 – x) + cotx}]
Solution:
We have,
limx→π/2[{(π/2 – x)sinx – 2cosx}/{(π/2 – x) + cotx}]
=![Rendered by QuickLaTeX.com \lim_{h\to0}\frac{[\frac{π}{2}-(\frac{π}{2}-h)]sin(\frac{π}{2}-h)-2cos(\frac{π}{2}-h)}{[\frac{π}{2}-(\frac{π}{2}-h)]+cot(\frac{π}{2}-h)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-507315d6b59ebe6f287b1abc2eae7b51_l3.png)
= limh→0[(hcosh-2sinh)/(h+tanh)]
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{cosh-2\frac{sinh}{h}}{1+\frac{tanh}{h}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85a926fba771094e7cb477b0cb00c2bc_l3.png) (On dividing the numerator and denominator by h)
(On dividing the numerator and denominator by h)
= (1 – 2)/(1 + 1)
= -1/2
Question 37. limx→π/4[(cosx – sinx)/{(π/4 – x)(cosx + sinx)}]
Solution:
We have,
limx→π/4[(cosx – sinx)/{(π/4 – x)(cosx + sinx)}]
On dividing the numerator and denominator by √2, we get
= ![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{4}}[\frac{\frac{cosx}{\sqrt2}-\frac{sinx}{\sqrt2}}{(\frac{π}{4}-x)(\frac{cosx+sinx}{\sqrt2})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3126bf9b2046fee36e1a14dff8bbf8b_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{4}}[\frac{{\sqrt2}(sin\frac{π}{4}.cosx-cos\frac{π}{4}.sinx)}{(\frac{π}{4}-x)(cosx+sinx)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-49777c7839fb8370b64b593ad89f8955_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to \frac{π}{4}}[\frac{{\sqrt2}[sin(\frac{π}{4}-x)]}{(\frac{π}{4}-x)(cosx+sinx)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c78773c10c8b47ada68a54b595ec07af_l3.png)
= ![Rendered by QuickLaTeX.com \sqrt2\lim_{x\to \frac{π}{4}}[\frac{[sin(\frac{π}{4}-x)]}{(\frac{π}{4}-x)}]\lim_{x\to \frac{π}{4}}[\frac{1}{(cosx+sinx)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-84c8e6bbe19e77545f0127c45e5880cb_l3.png)
= 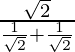
= (√2 × √2)/2
= 1
Question 38. limx→π[{1 – sin(x/2)}/{cos(x/2)(cosx/4 – sinx/4}]
Solution:
We have,
limx→π[{1 – sin(x/2)}/{cos(x/2)(cosx/4 – sinx/4}]
Let, x = π + h
If x→π, then h→0
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{1-sin(\frac{π+h}{2})}{cos(\frac{π+h}{2})[cos(\frac{π+h}{4})-sin(\frac{π+h}{4})]}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ecaee1a43200c4f17a9ae66bf3b1e371_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{1-sin(\frac{π}{2}+\frac{h}{2})}{cos(\frac{π}{4}+\frac{h}{2})[cos(\frac{π}{4}+\frac{h}{4})-sin(\frac{π}{4}+\frac{h}{4})]}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d442fa335899c40c6a4649c7f220c27f_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{1-cos(\frac{h}{2})}{-sin(\frac{h}{2})[-\sqrt{2}sin(\frac{h}{2})]}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b7fadbcc01a108dd81e1be7571ba6e41_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{2sin^2(\frac{h}{4})}{-sin(\frac{h}{2})[-\sqrt{2}sin(\frac{h}{4})]}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ede6855cd210c89cd861297df01841a8_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{2sin^2(\frac{h}{4})}{2sin(\frac{h}{4})cos(\frac{h}{4})[\sqrt{2}sin(\frac{h}{4})]}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f4ab704f591ef987ad863eda8c8091fe_l3.png)
= 
= 1/√2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...