Class 11 RD Sharma Solutions – Chapter 29 Limits – Exercise 29.6 | Set 2
Last Updated :
18 Apr, 2022
Question 14. Limn→∞{12 + 22 + ……………. + n2}/(n3)
Solution:
We have,
Limn→∞{12 + 22 + ……………. + n2}/(n3)
= Limn→∞[n(n+1)(2n+1)]/6n3
= Limn→∞[(n+1)(2n+1)]/6n2
=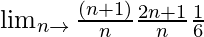
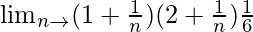
When n → ∞, (1/n) → 0
= 2/6
= 1/3
Question 15. Limn→∞{1 + 2 + 3 + 4 +……………. + n – 1}/n2
Solution:
We have,
Limn→∞{1 + 2 + 3 + 4 +……………. + n – 1}/n2
= Limn→∞[n(n – 1)/2n2]
= Limn→∞[n2 – n/2n2]
= Limn→∞(1/2 – 1/2n)
When n → ∞, (1/n) → 0
= 1/2
Question 16. Limn→∞{13 + 23 + ……………. + n3}/(n4)
Solution:
We have,
Limn→∞{13 + 23 + ……………. + n3}/(n4)
= Limn→∞[n2(n + 1)2]/(4n4) [since (13 + 23 + …………. + n3) = n2(n + 1)2/4]
= Limn→∞[(n + 1)2]/(4n2)
= Limn→∞[(1 + 1/n)2 × (1/4)]
When n → ∞, (1/n) → 0
= 1/4
Question 17. Limn→∞{13 + 23 + ……………. + n3}/(n – 1)4
Solution:
We have,
Limn→∞{13 + 23 + ……………. + n3}/(n – 1)4
= Limn→∞[n2(n + 1)2]/[4(n – 1)4] [since (13 + 23 + …………. + n3) = n2(n + 1)2/4]
=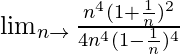
=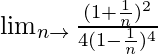
When n → ∞, (1/n) → 0
= 1/4
Question 18. Limx→∞[√x{√(x + 1) – √x}]
Solution:
We have,
Limx→∞[√x{√(x + 1) – √x}]
On rationalizing numerator, we get
= Limx→∞[(√x){(x + 1) – x}]/{√(x + 1) + √x}
= Limx→∞(√x}/{√(x + 1) + √x}
=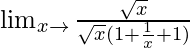
When x → ∞, (1/x) → 0.
= 1/(√1 + 1)
= 1/2
Question 19. Limx→∞[1/3 + 1/32 + 1/33 + ……………… + 1/3n]
Solution:
We have,
Limx→∞[1/3 + 1/32 + 1/33 + ……………… + 1/3n]
This is G.P series of common ratio 1/3.
So, the sum of n terms of G.P. Sn = [a(1 – rn)]/(1 – r) (i)
a = 1/3, r = 1/3
On putting the value of a & r in equation (i), we get
Sn = (1/2)(1 – 1/3n)
= Limx→∞[(1/2)(1 – 1/3n)]
= (1/2)Limx→∞(1 – 1/3n)
= (1/2)(1 – 0)
= 1/2
Question 20. Limx→∞{(x4 + 7x3 + 46x + a)}/{(x4 + 6)}.
Solution:
We have,
Limx→∞{(x4 + 7x3 + 46x + a)}/{(x4 + 6)}
=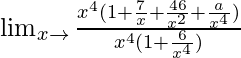
When x → ∞, (1/x), (1/x2), (1/x3), (1/x4) → 0
= 1/1
= 1
Question 21. f(x) = (ax2 + b)/(x2 + 1), Limx→0f(x) = 1, Limx→∞f(x) = 1, then prove that f(-2) = f(2) = 1
Solution:
We have,
f(x) = (ax2 + b)/(x2 + 1)
= Limx→0[(ax2 + b)/(x2 + 1)]
b/1 = 1
b = 1
= Limx→∞[(ax2 + b)/(x2 + 1)]
= 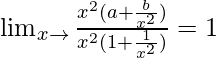
When x → ∞, (1/x2) → 0.
(a + 0)/(1 + 0) = 1
a = 1
Hence, a = 1, b = 1
f(x) = (x2 + 1)/(x2 + 1)
f(x) = 1
f(-2) = 1
f(2) = 1 (Since f(x) is independent on x)
f(-2) = f(2) = 1
Hence proved
Question 22. Show that Limx→∞[√(x2 + x + 1) – x] ≠ Limx→∞[√(x2 + 1) – x]
Solution:
We have,
L.H.S,
= Limx→∞[√(x2 + x + 1) – x]
On rationalizing numerator, we get
= Limx→∞[(x2 + x + 1) – x2]/[√(x2 + x + 1) + x]
= Limx→∞(x + 1)/[√(x2 + x + 1) + x]
= Limx→∞[x(1 + 1/x)/[x{√(1 + 1/x + 1/x2) + 1}]
= Limx→∞[(1 + 1/x)/[{√(1 + 1/x + 1/x2) + 1}]
When x → ∞, (1/x), (1/x2) → 0.
= 1/(√1 + 1)
= 1/2
Now we solve R.H.S,
= Limx→∞[√(x2 + 1) – x]
On rationalizing numerator, we get
= Limx→∞[(x2 + 1) – x2]/[√(x2 + 1) + x]
= Limx→∞(1)/[√(x2 + 1) + x]
= 1/[√(∞ + 1) + ∞]
= 1/∞
= 0
L.H.S ≠ R.H.S
Hence, Limx→∞[√(x2 + x + 1) – x] ≠ Limx→∞[√(x2 + 1) – x]
Question 23. Limx→-∞[√(4x2 – 7x) + 2x]
Solution:
We have,
Limx→-∞[√(4x2 – 7x) + 2x]
Let x = -n when x → -∞, then n → ∞.
= Limn→∞[√(4n2 + 7n) – 2n]
On rationalizing numerator, we get
= Limn→∞[(4n2 + 7n) – 4n2]/[√(4n2 + 7n) + 2n]
= Limn→∞[(7n)/[√(4n2 + 7n) + 2n]
= Limn→∞(7n)/[n{√(4 + 7/n) + 2}]
= Limn→∞(7)/{√(4 + 7/n) + 2}
When n → ∞, (1/n) → 0
= 7/(√4 + 2)
= 7/(2 + 2)
= 7/4
Question 24. Limx→-∞[√(x2 – 8x) + x]
Solution:
We have,
Limx→-∞[√(x2 – 8x) + x]
Let x = -n when x → -∞, then n → ∞.
= Limn→∞[√(n2 + 8n) – n]
On rationalizing numerator, we get
= Limn→∞[(n2 + 8n) – n2]/[√(n2 + 8n) + n]
= Limn→∞[(8n)/[√(n2 + 8n) + n]
= Limn→∞(8n)/[n{√(1 + 8/n) + 1}]
= Limn→∞(8)/{√(1 + 8/n) + 1}
When n → ∞, (1/n) → 0
= 8/(√1 + 1)
= 8/2
= 4
Question 25. Limn→∞(14 + 24 + ……….+ n4)/n5 – Limn→∞(13 + 23 + ………. + n3)/n5
Solution:
We have,
Limn→∞(14 + 24 + ……….+ n4)/n5 – Limn→∞(13 + 23 + ………. + n3)/n5
=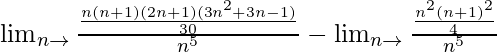
=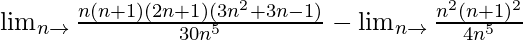
=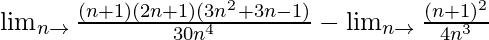
=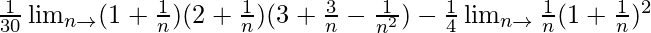
When n → ∞, (1/n), (1/n2), (1/n3) → 0
= 1/3 × 1 × 2 × 3 – 1/4 × 0
= 6/30
= 1/5
Question 26. Limn→∞{(1.2 + 2.3 + 3.4 + ……….+ n (n + 1)}/n3
Solution:
We have,
Limn→∞{(1.2 + 2.3 + 3.4 + ……….+ n (n + 1)}/n3
=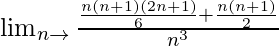
=![Rendered by QuickLaTeX.com \lim_{n\to∞}\frac{n(n+1)[\frac{(2n+1)+3}{6}]}{n^3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69aef80edc54b5caf591d4beecbc6746_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to∞}\frac{n(n+1)[\frac{(2n+4)}{6}]}{n^3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7c6ceafa6549ef42f97ce97fda491ab9_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to∞}\frac{n(n+1)[(2n+4)]}{6n^3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8133eb7a0d6e7a070725ea258de409b5_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to∞}\frac{n(n+1)[(2n+4)]}{6n^3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8133eb7a0d6e7a070725ea258de409b5_l3.png)
=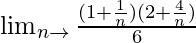
When n → ∞, (1/n) → 0
= (1 × 2)/6
= 2/6
= 1/3
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...