Evaluates the following limits:
Question 1. Limx→0{√(1 + x + x2) – 1}/x.
Solution:
We have, Limx→0{√(1 + x + x2) – 1}/x
Find the limit of the given equation when x =>0.
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 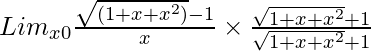
= Limx→0(1 + x + x2 – 1)/{x√(1 + x + x2) + 1}
= Limx→0{x(x + 1)}/{x√(1 + x + x2) + 1}
= Limx→0(x + 1)/{√(1 + x + x2) + 1}
Now put x = 0, we get
= (0 + 1)/{√(1 + 0 + 0) + 1}
= 1/2
Question 2. Limx→0(2x)/{√(a + x) – √(a – x)}
Solution:
We have, Limx→0(2x)/{√(a + x) – √(a – x)}
Find the limit of the given equation when x =>0.
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 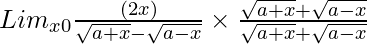
= Limx→0[2x{√(a + x) + √(a – x)}]/{(a + x) – (a – x)}
= Limx→0[2x{√(a + x) + √(a – x)}]/2x
= Limx→0{√(a + x) + √(a – x)}
Now put x = 0, we get
= √a + √a
= 2√a
Question 3. Limx→0{√(a2 + x2) – a}/x2
Solution:
We have, Limx→0{√(a2 + x2) – a}/x2
Find the limit of the given equation when x =>0.
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 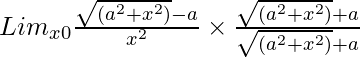
= Limx→0(a2 + x2 – a2)/[x2{√(a2 + x2) + a}]
= Limx→0(x2)/[x2{√(a2 + x2) + a}]
= Limx→0(1)/{√(a2 + x2) + a}
Now put x = 0, we get
= 1/(a + a)
= 1/2a
Question 4. Limx→0{√(1 + x) – √(1 – x)}/2x
Solution:
We have, Limx→0{√(1 + x) – √(1 – x)}/2x
Find the limit of the given equation when x =>0.
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 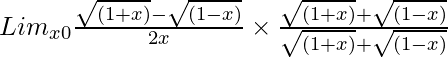
= Limx→0(1 + x – 1 + x)/[2x{√(1 + x) + √(1 – x)}]
= Limx→0(2x)/[2x{√(1 + x) + √(1 – x)}]
= Limx→0(1)/{√(1 + x) + √(1 – x)}
Now put x = 0, we get
= 1/(1 + 1)
= 1/2
Question 5. Limx→2{√(3 – x) – 1}/(2 – x)
Solution:
We have, Limx→2{√(3 – x) – 1}/(2 – x)
Find the limit of the given equation
When we put x = 2, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 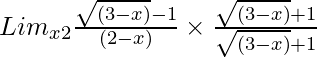
= Limx→2{(3 – x) – 1}/[(2 – x){√(3 – x) + 1}]
= Limx→2(2 – x)/[(2 – x){√(3 – x) + 1}]
= Limx→2(1)/{√(3 – x) + 1}
Now put x = 2, we get
= 1/{√(3 – 2) + 1}
= 1/(1 + 1)
= 1/2
Question 6. Limx→3(x – 3)/{√(x – 2) – √(4 – x)}
Solution:
We have, Limx→3(x – 3)/{√(x – 2) – √(4 – x)}
Find the limit of the given equation
When we put x = 3, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 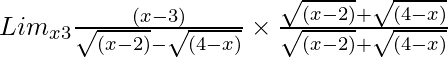
= Limx→3[(x – 3){√(x – 2) + √(4 – x)}]/{(x – 2) – (4 – x)}
= Limx→3[(x – 3){√(x – 2) + √(4 – x)}]/{2(x – 3)}
= Limx→3{√(x – 2) + √(4 – x)}/2
Now put x = 3, we get
= {√(3 – 2) + √(4 – 3)}/2
= (1 + 1)/2
= 1
Question 7. Limx→0(x)/{√(1 + x) – √(1 – x)}
Solution:
We have, Limx→0(x)/{√(1 + x) – √(1 – x)}
Find the limit of the given equation
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 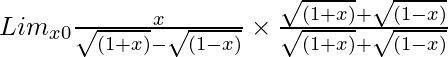
= Limx→0[x{√(1 + x) + √(1 – x)}]/{(1 + x) – (1 – x)}
= Limx→0[x{√(1 + x) + √(1 – x)}]/(2x)
= Limx→0{√(1 + x) + √(1 – x)}/(2)
Now put x = 0, we get
= (√1 + √1)/2
= 2/2
= 1
Question 8. Limx→1{√(5x – 4) – √x}/(x – 1)
Solution:
We have, Limx→1{√(5x – 4) – √x}/(x – 1)
Find the limit of the given equation
When we put x = 1, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 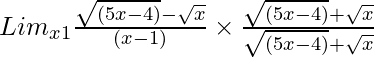
= Limx→1{5x – 4 – x}/[(x – 1){√(5x – 4) + √x}]
= Limx→1{4(x – 1)}/[(x – 1){√(5x – 4) + √x}]
= Limx→1(4)/{√(5x – 4) + √x}
Now put x = 1, we get
= 4/{√(5 – 4) + √1}
= 4/(1 + 1)
= 2
Question 9. Limx→1(x – 1)/{√(x2 + 3) – 2}
Solution:
We have, Limx→1(x – 1)/{√(x2 + 3) – 2}
Find the limit of the given equation
When we put x = 1, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 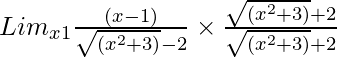
= Limx→1[(x – 1){√(x2 + 3) + 2}]/{(x2 + 3) – 4}
= Limx→1[(x – 1){√(x2 + 3) + 2}]/(x2 – 1)
= Limx→1[(x – 1){√(x2 + 3) + 2}]/{(x – 1)(x + 1)}
= Limx→1{√(x2 + 3) + 2}/{(x + 1)}
Now put x = 1, we get
= {√(1 + 3) + 2}/(1 + 1)
= (2 + 2)/2
= 2
Question 10. Limx→3{√(x + 3) – √6}/(x2 – 9)
Solution:
We have, Limx→3{√(x + 3) – √6}/(x2 – 9)
Find the limit of the given equation
When we put x = 3, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 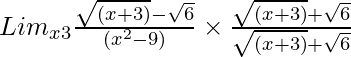
= Limx→3{(x + 3) – 6}/[(x2 – 9){√( x+ 3) + √6}]
= Limx→3(x – 3)/[(x – 3)(x + 3){√(x + 3) + √6}]
= Limx→3(1)/[(x + 3){√(x + 3) + √6}]
Now put x = 3, we get
= 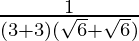
= 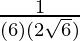
= 1/(12√6)
Question 11. Limx→1{√(5x – 4) – √x}/(x2 – 1)
Solution:
We have, Limx→1{√(5x – 4) – √x}/(x2 – 1)
Find the limit of the given equation
When we put x = 1, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 
= Limx→1{5x – 4 – x}/[(x2 – 1){√(5x – 4) + √x}]
= Limx→1{4(x – 1)}/[(x – 1)(x + 1){√(5x – 4) + √x}]
= Limx→1(4)/[{√(5x – 4) + √x}(x + 1)]
Now put x = 1, we get
= 4/[{√(5 – 4) + √1}(1 + 1)]
= 4/[(1 + 1)(1 + 1)]
= 4/4
= 1
Question 12. Limx→0{√(1 + x) – 1}/x
Solution:
We have, Limx→0{√(1 + x) – 1}/x
Find the limit of the given equation
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 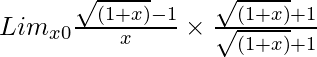
= Limx→0(1 + x – 1)/[x{√(1 + x) + 1}]
= Limx→0(x)/[x{√(1 + x) + 1}]
= Limx→0(1)/{√(1 + x) + 1}
Now put x = 0, we get
= 1/(1 + 1)
= 1/2
Question 13. Limx→2{√(x2 + 1) – √5}/(x – 2)
Solution:
We have, Limx→2{√(x2 + 1) – √5}/(x – 2)
Find the limit of the given equation
When we put x = 2, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 
= Limx→2{x2 + 1 – 5}/[(x – 2){√(x2 + 1) + √5}]
= Limx→2{(x2 – 4)}/[(x – 2){√(x2 + 1) + √5}]
= Limx→2{(x – 2)(x + 2)}/[(x – 2){√(x2 + 1) + √5}]
= Limx→2{(x + 2)}/{√(x2 + 1) + √5}
Now put x = 2, we get
= 4/{√(5) + √5}
= 4/(2√5)
= 2/(√5)
Question 14. Limx→2(x – 2)/{√x – √2}
Solution:
We have, Limx→2(x – 2)/{√x – √2}
Find the limit of the given equation
When we put x = 2, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 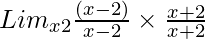
= Limx→2[(x – 2){√x + √2}]/{x – 2}
= Limx→2{√x + √2}
Now put x = 2, we get
= √2 + √2
= 2√2
Question 15. Limx→7{4 – √(9 + x)}/{1 – √(8 – x)}
Solution:
We have, Limx→7{4 – √(9 + x)}/{1 – √(8 – x)}
Find the limit of the given equation
When we put x = 7, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
=
=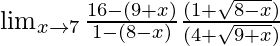
=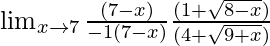
Now put x = 7, we get
= -{1 + √(8 – 7)}/{4 + √(9 + 7)}
= -2/(4 + 4)
= -1/4
Question 16. Limx→0{√(a + x) – √a}/[x{√(a2 + ax)}]
Solution:
We have,
Limx→0{√(a + x) – √a}/[x{√(a2 + ax)}]
Find the limit of the given equation
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 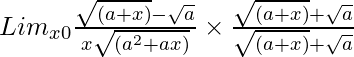
= Limx→0{(a + x) – a}/[x{√(a2 + ax)}{√(a + x) + √a}]
= Limx→0(x)/[x{√(a2 + ax)}{√(a + x) + √a}]
= Limx→0(1)/[{√(a2 + ax)}{√(a + x) + √a}]
Now put x = 0, we get
= 1/{a.(√a + √a)}
= 1/(2a√a)
Question 17. Limx→7(x – 5)/{√(6x – 5) – √(4x + 5)}
Solution:
We have, Limx→7(x – 5)/{√(6x – 5) – √(4x + 5)}
Find the limit of the given equation
When we put x = 7, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 
= Limx→7[{√(6x – 5) + √(4x + 5)}(x – 5)]/{(6x-5) – (4x + 5)}
= Limx→7[{√(6x – 5) + √(4x + 5)}(x – 5)]/{2(x – 5)}
= Limx→7[{√(6x – 5) + √(4x + 5)}]/(2)
Now put x = 7, we get
= {√(6 × 7 – 5) + √(4 × 7 + 5)}/(2)
= (5 + 5)/2
= 5
Share your thoughts in the comments
Please Login to comment...