Class 11 RD Sharma Solutions – Chapter 29 Limits – Exercise 29.10 | Set 3
Last Updated :
04 May, 2021
Evaluate the following limits:
Question 31.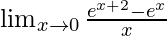
Solution:
We have,
=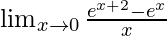
=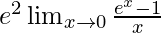
We know,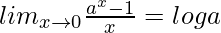 . So, we have,
. So, we have,
= e2 × log e
= e2
Question 32.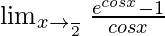
Solution:
We have,
=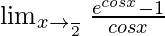
Let x − π/2 = h. So, we get
=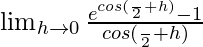
=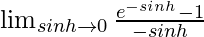
We know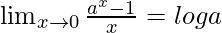 . So, we get,
. So, we get,
= log e
= 1
Question 33.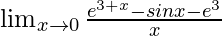
Solution:
We have,
=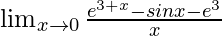
=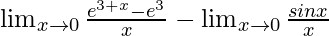
=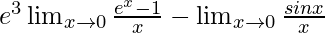
We know,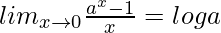 and
and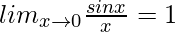 . So, we have,
. So, we have,
= e3 log e − 1
= e3 − 1
Question 34.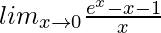
Solution:
We have,
=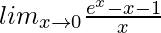
=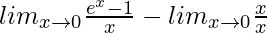
=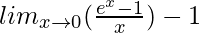
We know,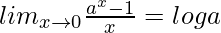 . So, we have,
. So, we have,
= log e − 1
= 1 − 1
= 0
Question 35.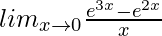
Solution:
We have,
=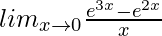
=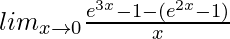
=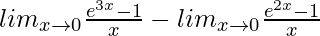
=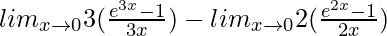
We know,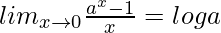 . So, we have,
. So, we have,
= 3 log e − 2 log e
= 3 − 2
= 1
Question 36.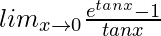
Solution:
We have,
=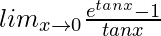
=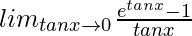
We know,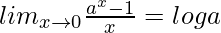 . So, we have,
. So, we have,
= log e
= 1
Question 37.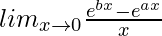 , 0 < a < b
, 0 < a < b
Solution:
We have,
=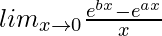
=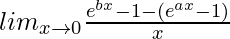
=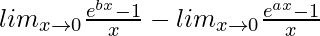
=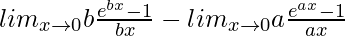
We know,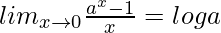 . So, we have,
. So, we have,
= b log e − a log e
= b − a
Question 38.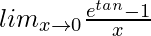
Solution:
We have,
=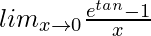
=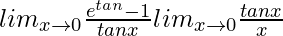
We know,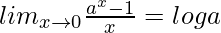 and
and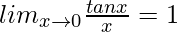 . So, we have,
. So, we have,
= log e × 1
= 1
Question 39.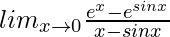
Solution:
We have,
=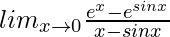
=![Rendered by QuickLaTeX.com lim_{x\to0}e^{sinx}\left[\frac{e^{x-sinx}-1}{x-sinx}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-88d133601123c412f5fad65b440b8bc6_l3.png)
=![Rendered by QuickLaTeX.com lim_{x\to0}e^{sinx}×lim_{x\to0}\left[\frac{e^{x-sinx}-1}{x-sinx}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bc626754224e032257818fc26bb62b40_l3.png)
We know,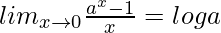 . So, we have,
. So, we have,
=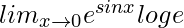
= e0
= 1
Question 40.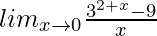
Solution:
We have,
=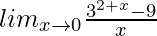
=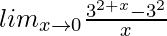
=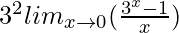
We know,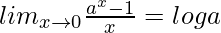 . So, we have,
. So, we have,
= 9 × log 3
= 9 log 3
Question 41.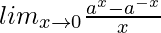
Solution:
We are given,
=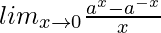
=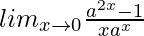
=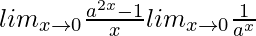
=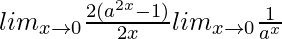
We know,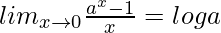 . So, we have,
. So, we have,
=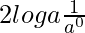
= 2 log a
Question 42.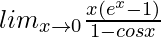
Solution:
We have,
=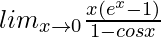
=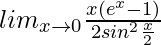
=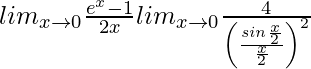
We know,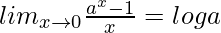 and
and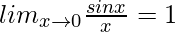 . So, we have,
. So, we have,
=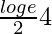
= 2
Question 43.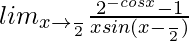
Solution:
We have,
=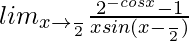
=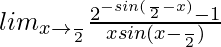
=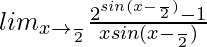
=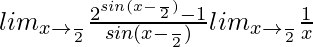
Let x− π/2 = h in first part. So, we get,
=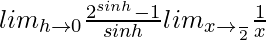
We know,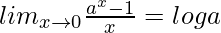 . So, we have,
. So, we have,
=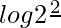
=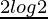
=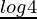
Share your thoughts in the comments
Please Login to comment...