Question 13. Prove that the tetrahedron with vertices at points O(0,0,0), A(0,1,1), B(1,0,1) and C(1,1,0) is a regular one.
Solution:
Given: The points O(0,0,0), A(0,1,1), B(1,0,1) and C(1,1,0).
A regular tetrahedron has all equal sides and diagonals.
We know that the distance between two points (a, b, c) and (d, e, f) is given as follows:

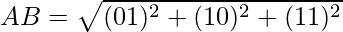
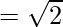
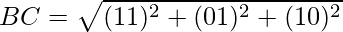
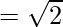

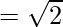
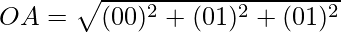
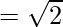
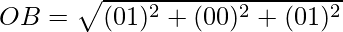
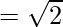
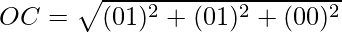
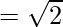
Clearly, OA = OB = OC = AB = BC = CA.
Hence O, A, B and C represent a regular tetrahedron.
Question 14. Show that the points (3,2,2), (-1,1,3), (0,5,6), (2,1,2) lie on a sphere whose centre is (1,3,4). Also find its radius.
Solution:
Given: The points A(3,2,2), B(-1,1,3), C(0,5,6), D(2,1,2) and E(1,3,4)
We know that the distance between two points (a, b, c) and (d, e, f) is given as follows:

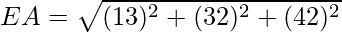
= 3
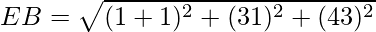
= 3
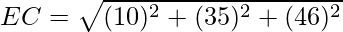
= 3
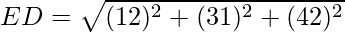
= 3
Since EA = EB = EC = ED, the points lie on a sphere with centre E.
Radius of the sphere = 3 units.
Question 15. Find the coordinates of the point which is equidistant from the four points O(0,0,0), A(2,0,0), B(0,3,0) and C(0,0,8).
Solution:
Given: Points O(0,0,0), A(2,0,0), B(0,3,0) and C(0,0,8).
Let the required point be P(x,y,z).
We are given that OP = PA ⇒ OP2 = PA2
Using formula, we have:
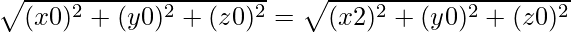
⇒ x2 + y2 + z2 = x2 − 4x + 4 + y2 +z2
⇒ 4x = 4
⇒ x = 1
Similarly, OP2 = PB2
⇒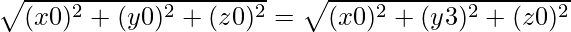
⇒ x2 + y2 + z2 = x2 + y2 − 6y +9 +z2
⇒ 6y = 9
⇒ y = 3/2
Also, OP2 = PC2
⇒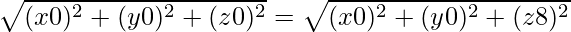
⇒ x2 + y2 + z2 = x2 + y2 +z2 − 16z + 64
⇒ 16z = 64
⇒ z = 4
Hence the point is P[1, 3/2, 4].
Question 16. If A(-2,2,3) and B(13,-3,13) are two points, find the locus of a point P which moves in a way such that 3PA = 2PB.
Solution:
Given: A(-2,2,3) and B(13,-3,13)
Let P = (x, y, z) be the required point.
We are given 3PA = 2PB
Using the formula,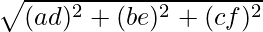 , we have:
, we have:
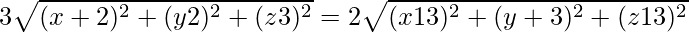
Squaring both sides, we have;
9(x2 + 4x +4 + y2 + 4 − 4y + z2 + 9 − 6z) = 4(x2 + 169 − 26x + y2 +9 + 6y + z2 + 169 − 26z)
⇒ 5(x2 + y2 +z2) + 140x − 60y + 50z − 1235 = 0.
Question 17. Find the locus of P if PA2 + PB2 = 2k2, where A and B are the points (3,4,5) and (-1,3,-7).
Solution:
Given: A(3,4,5) and B(-1,3,-7)
Let P(x, y, z) be the required point.
PA2 + PB2 = 2k2. Using the formula,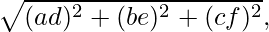 we have:
we have:
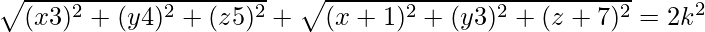
⇒ 2x2 + 2y2 + 2z2 − 4x −14y + 4z + 109 − 2k2 = 0
⇒ 2(x2 + y2 +z2) − 4x −14y + 4z + 109 − 2k2 = 0.
Question 18. Show that the points A(a, b, c), B(b, c, a) and C(c, a, b) are vertices of an equilateral triangle.
Solution:
Given: points A(a, b, c), B(b, c, a) and C(c, a, b)
Using formula, distance between two points (a, b, c) and (d, e, f) is given as follows:


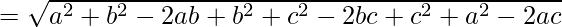
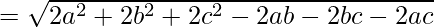
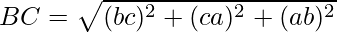
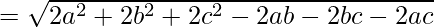
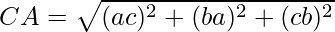
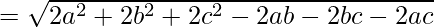
Since AB = BC = CA
ABC is an equilateral triangle.
Question 19. Are points A(3,6,9), B(10,20,30), and C(25,41,5) the vertices of a right-angled triangle?
Solution:
Given: A(3,6,9), B(10,20,30) and C(25,41,5)
Using formula, distance between two points (a, b, c) and (d, e, f) is given as follows:


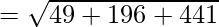
⇒ AB2 = 586
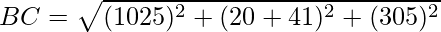
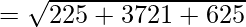
⇒ BC2 = 4571
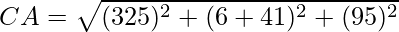
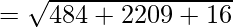
⇒ CA2 = 2709
Since, AB2 + BC2 ≠ AC2
AB2 + AC2 ≠ BC2
BC2 + AC2 ≠ AB2
ABC is not a right triangle.
Question 20. Verify that:
(i) (0,7,-10), (1,6,-6) and (4,9,-6) are the vertices of an isosceles triangle.
Solution:
Given: A(0,7,-10), B(1,6,-6) and C(4,9,-6)
Using formula, distance between two points (a, b, c) and (d, e, f) is given as follows:

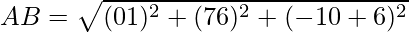
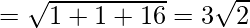
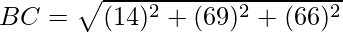
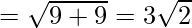
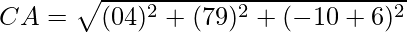
= 6
Since AB = BC, ABC is an isosceles triangle.
(ii) (0,7,-10), (-1,6,6) and (4,9,-6) are the vertices of a right-angled triangle.
Solution:
Given: Given: A(0,7,-10), B(1,6,-6) and C(4,9,-6)
Using formula, distance between two points (a, b, c) and (d, e, f) is given as follows:


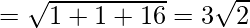
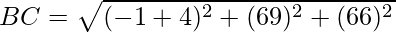
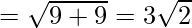
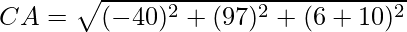
= 6
Since AB2 + BC2 = AC2, ABC is a right triangle.
(iii) (-1,2,1), (1,-2,5), (4,-7,8) and (2,-3,4) are the vertices of a parallelogram.
Solution:
Given: A(-1,2,1), B(1,-2,5), C(4,-7,8) and D(2,-3,4)
Using formula, distance between two points (a, b, c) and (d, e, f) is given as follows:



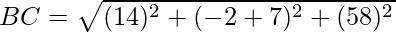
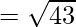
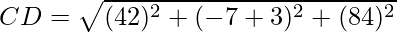

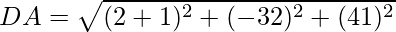
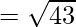
Since the opposite sides are equal, ABCD is a parallelogram.
(iv) (5,-1,1), (7,-4,7), (1,-6,10) and (-1,-3,4) are vertices of a rhombus.
Solution:
Given: A(5,-1,1), B(7,-4,7), C(1,-6,10) and D(-1,-3,4)
Using formula, distance between two points (a, b, c) and (d, e, f) is given as follows:

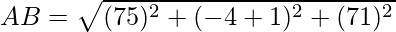
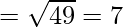
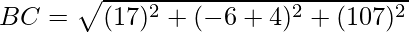
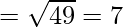
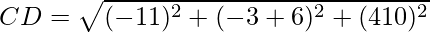
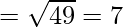

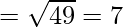
Since AB = BC = CA = AD
ABCD is a rhombus.
Question 21. Find the locus of the points which are equidistant from the points (1,2,3) and (3,2,-1).
Solution:
Let P(x, y, z) be the point equidistant from the points A(1,2,3) and B(3,2,-1).
Using formula, distance between two points (a, b, c) and (d, e, f) is given as follows:

⇒ AP = BP or AP2 = BP2
⇒ (x − 1)2 + (y − 2)2 + (z − 3)2 = (x − 3)2 + (y − 2)2 + (z + 1)2
⇒ 4x − 8z = 14 − 14
⇒ x − 2z = 0.
Question 22. Show that the points A(1,2,3), B(-1.-2,-1), C(2,3,2) and D(7,4,6) are the vertices of a parallelogram ABCD.
Solution:
Using formula, distance between two points (a, b, c) and (d, e, f) is given as follows:

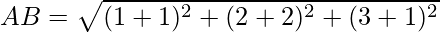

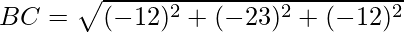
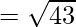
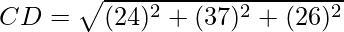


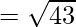
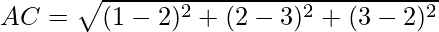

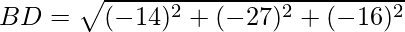
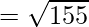
Since the opposite sides are equal, ABCD is a parallelogram.
Question 23: Find the locus of the point, the sum of whose distances from the points A(4,0,0) and B(-4,0,0) is equal to 10.
Solution:
Let P(x, y, z) be the required locus.
Given: PA + PB = 10. Using distance formula,

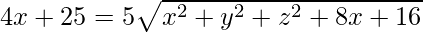
Squaring both sides, we get
16x2 + 625 + 200x = 25(x2 + y2 + z2 + 8x + 16)
⇒ 9x2 + 25y2 + 25z2 – 225 = 0
Question 24. Find the equation of the set of points P such that its distances from the points A(3,4,-5) and B(-2,1,4) are equal.
Solution:
Given: A(3,4,-5) and B(-2,1,4)
Let P(x, y, z) be the required point, It is given that PA = PB.
Hence, PA2 = PB2
Using distance formula, we have,
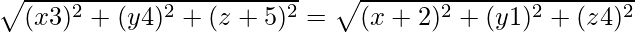
⇒ -6x + 9 – 8y + 16 + 10z + 25 = 4x + 4 – 2y +1 – 8z +16
⇒ 10x + 6y – 18z -29 = 0.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...