Question 1. The equation of the directrix of a hyperbola is x – y + 3 = 0. Its focus is (-1, 1) and eccentricity 3. Find the equation of the hyperbola.
Solution:
Given: Focus = (-1, 1) and Eccentricity = 3
The equation of the directrix of a hyperbola ⇒ x – y + 3 = 0.
Let ‘M’ be the point on directrix and P(x, y) be any point of the hyperbola.
We know, e = PF/PM ⇒ PF2 = e2PM2
![Rendered by QuickLaTeX.com ⇒ (x+1)^2 + (y-1)^2 = 3^2[\frac{x-y+3}{\sqrt{1^2+(-1)^2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85818ab45cfd3ce86d82a1309d814825_l3.png)
⇒ 2{x2 + 1 + 2x + y2 + 1 – 2y} = 9{x2 + y2+ 9 + 6x – 6y – 2xy}
⇒ 2x2 + 2 + 4x + 2y2 + 2 – 4y = 9x2 + 9y2+ 81 + 54x – 54y – 18xy
⇒ 2x2 + 4 + 4x + 2y2– 4y – 9x2 – 9y2 – 81 – 54x + 54y + 18xy = 0
⇒ – 7x2 – 7y2 – 50x + 50y + 18xy – 77 = 0
⇒ 7(x2 + y2) – 18xy + 50x – 50y + 77 = 0
∴The equation of hyperbola is 7(x2 + y2) – 18xy + 50x – 50y + 77 = 0.
Question 2. Find the equation of the hyperbola whose
(i) focus is (0, 3), directrix is x + y – 1 = 0 and eccentricity = 2
Solution:
Given: Focus = (0, 3), Directrix => x + y – 1 = 0 and Eccentricity = 2
Let ‘M’ be the point on directrix and P(x, y) be any point of the hyperbola.
We know, e = PF/PM ⇒ PF2 = e2PM2
![Rendered by QuickLaTeX.com ⇒ (x-0)^2 + (y-3)^2 = 2^2[\frac{x+y-1}{\sqrt{1^2+(1)^2}}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d94f3759ff4b004b8c364aa397085ce_l3.png)
⇒ 2{x2 + y2 + 9 – 6y} = 4{x2 + y2 + 1 – 2x – 2y + 2xy}
⇒ 2x2 + 2y2 + 18 – 12y – 4x2 – 4y2 – 4 – 8x + 8y – 8xy = 0
⇒ – 2x2 – 2y2 – 8x – 4y – 8xy + 14 = 0
⇒ –2(x2 + y2 – 4x + 2y + 4xy – 7) = 0
⇒ x2 + y2 – 4x + 2y + 4xy – 7 = 0
∴The equation of hyperbola is x2 + y2 – 4x + 2y + 4xy – 7 = 0.
(ii) focus is (1, 1), directrix is 3x + 4y + 8 = 0 and eccentricity = 2
Solution:
Focus = (1, 1), Directrix => 3x + 4y + 8 = 0 and Eccentricity = 2
Let ‘M’ be the point on directrix and P(x, y) be any point of the hyperbola.
We know, e = PF/PM ⇒ PF2 = e2PM2
![Rendered by QuickLaTeX.com ⇒ (x-1)^2 + (y-1)^2 = 2^2[\frac{3x+4y+8}{\sqrt{3^2+(4)^2}}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4c883315c85e6b3c5ac586830a30fe89_l3.png)
⇒ 25{x2 + 1 – 2x + y2 + 1 – 2y} = 4{9x2 + 16y2+ 64 + 24xy + 64y + 48x}
⇒ 25x2 + 25 – 50x + 25y2 + 25 – 50y = 36x2 + 64y2 + 256 + 96xy + 256y + 192x
⇒ 25x2 + 25 – 50x + 25y2 + 25 – 50y – 36x2 – 64y2 – 256 – 96xy – 256y – 192x = 0
⇒ – 11x2 – 39y2 – 242x – 306y – 96xy – 206 = 0
⇒ 11x2 + 96xy + 39y2 + 242x + 306y + 206 = 0
∴The equation of hyperbola is 11x2 + 96xy + 39y2 + 242x + 306y + 206 = 0.
(iii) focus is (1, 1) directrix is 2x + y = 1 and eccentricity = 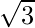
Solution:
Given: Focus = (1, 1), Directrix => 2x + y = 1 and Eccentricity = 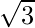
Let ‘M’ be the point on directrix and P(x, y) be any point of the hyperbola.
We know, e = PF/PM ⇒ PF2 = e2PM2
![Rendered by QuickLaTeX.com ⇒ (x-1)^2 + (y-1)^2 = (\sqrt{3})^2[\frac{2x+y-1}{\sqrt{2^2+(1)^2}}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e6f46cf6e3b6fa573d145178c37e6ba1_l3.png)
⇒ 5{x2 + 1 – 2x + y2 + 1 – 2y} = 3{4x2 + y2+ 1 + 4xy – 2y – 4x}
⇒ 5x2 + 5 – 10x + 5y2 + 5 – 10y = 12x2 + 3y2 + 3 + 12xy – 6y – 12x
⇒ 5x2 + 5 – 10x + 5y2 + 5 – 10y – 12x2 – 3y2 – 3 – 12xy + 6y + 12x = 0
⇒ – 7x2 + 2y2 + 2x – 4y – 12xy + 7 = 0
⇒ 7x2 + 12xy – 2y2 – 2x + 4y– 7 = 0
∴The equation of hyperbola is 7x2 + 12xy – 2y2 – 2x + 4y– 7 = 0.
(iv) focus is (2, -1), directrix is 2x + 3y = 1 and eccentricity = 2
Solution:
Given: Focus = (2, -1), Directrix => 2x + 3y = 1 and Eccentricity = 2
Let ‘M’ be the point on directrix and P(x, y) be any point of the hyperbola.
By using the formula, e = PF/PM ⇒ PF2 = e2PM2
![Rendered by QuickLaTeX.com ⇒ (x-2)^2 + (y+1)^2 = 2^2[\frac{2x+3y-1}{\sqrt{2^2+(3)^2}}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a7c1188367648545f343cc6988a2d05_l3.png)
⇒ 13{x2 + 4 – 4x + y2 + 1 + 2y} = 4{4x2 + 9y2 + 1 + 12xy – 6y – 4x}
⇒ 13x2 + 52 – 52x + 13y2 + 13 + 26y = 16x2 + 36y2 + 4 + 48xy – 24y – 16x
⇒ 13x2 + 52 – 52x + 13y2 + 13 + 26y – 16x2 – 36y2 – 4 – 48xy + 24y + 16x = 0
⇒ – 3x2 – 23y2 – 36x + 50y – 48xy + 61 = 0
⇒ 3x2 + 23y2 + 48xy + 36x – 50y– 61 = 0
∴The equation of hyperbola is 3x2 + 23y2 + 48xy + 36x – 50y– 61 = 0.
(v) focus is (a, 0), directrix is 2x + 3y = 1 and eccentricity = 2
Solution:
Given: Focus = (a, 0), Directrix => 2x + 3y = 1 and Eccentricity = 2
Let ‘M’ be the point on directrix and P(x, y) be any point of the hyperbola.
By using the formula, e = PF/PM ⇒ PF2 = e2PM2
![Rendered by QuickLaTeX.com ⇒ (x-a)^2 + (y-0)^2 = (4/3)^2[\frac{2x-y+a}{\sqrt{2^2+(-1)^2}}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-02f2a65f05cc9670500def64a9c22055_l3.png)
⇒ 45{x2 + a2 – 2ax + y2} = 16{4x2 + y2 + a2 – 4xy – 2ay + 4ax}
⇒ 45x2 + 45a2 – 90ax + 45y2 = 64x2 + 16y2 + 16a2 – 64xy – 32ay + 64ax
⇒ 45x2 + 45a2 – 90ax + 45y2 – 64x2 – 16y2 – 16a2 + 64xy + 32ay – 64ax = 0
⇒ 19x2 – 29y2 + 154ax – 32ay – 64xy – 29a2 = 0
∴The equation of hyperbola is 19x2 – 29y2 + 154ax – 32ay – 64xy – 29a2 = 0.
(vi) focus is (2, 2), directrix is x + y = 9 and eccentricity = 2
Solution:
Given: Focus = (2, 2), Directrix => x + y = 9 and Eccentricity = 2
Let ‘M’ be the point on directrix and P(x, y) be any point of the hyperbola.
By using the formula, e = PF/PM ⇒ PF2 = e2PM2
![Rendered by QuickLaTeX.com ⇒ (x-2)^2 + (y-2)^2 = (2)^2[\frac{x+y-9}{\sqrt{1^2+(1)^2}}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-651925d80f54f1ffb2ce2a2e78d3c71e_l3.png)
⇒ x2 + 4 – 4x + y2 + 4 – 4y = 2{x2 + y2 + 81 + 2xy – 18y – 18x}
⇒ x2 – 4x + y2 + 8 – 4y = 2x2 + 2y2 + 162 + 4xy – 36y – 36x
⇒ x2 – 4x + y2 + 8 – 4y – 2x2 – 2y2 – 162 – 4xy + 36y + 36x = 0
⇒ – x2 – y2 + 32x + 32y + 4xy – 154 = 0
⇒ x2 + 4xy + y2 – 32x – 32y + 154 = 0
∴The equation of hyperbola is x2 + 4xy + y2 – 32x – 32y + 154 = 0.
Question 3. Find the eccentricity, coordinates of the foci, equations of directrices, and length of the latus-rectum of the hyperbola.
(i) 9x2 – 16y2 = 144
Solution:
Given: 9x2 – 16y2 = 144
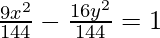
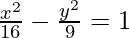
This is of the form 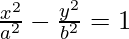 where, a2 = 16, b2 = 9 i.e., a = 4 and b = 3
where, a2 = 16, b2 = 9 i.e., a = 4 and b = 3
Eccentricity is given by:
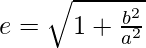


Eccentricity 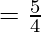
Foci: The coordinates of the foci are (±ae, 0)
Foci = (±5, 0)
The equation of directrices is given as: 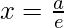 ⇒ 5x ∓ 16 = 0
⇒ 5x ∓ 16 = 0
The length of latus-rectum is given as: 2b2/a = 2(9)/4
Length of latus rectum= 9/2
(ii) 16x2 – 9y2 = –144
Solution:
Given: 16x2 – 9y2 = –144
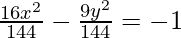
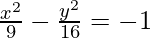
This is of the form 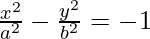 where, a2 = 9, b2 = 16 i.e., a = 3 and b = 4.
where, a2 = 9, b2 = 16 i.e., a = 3 and b = 4.
Eccentricity is given by:
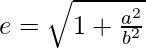


Eccentricity = 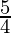
Foci: The coordinates of the foci are (0, ±be)
(0, ±be) = (0, ±4(5/4))
= (0, ±5).
The equation of directrices is given as: x =  ⇒ 5x ∓ 16 = 0.
⇒ 5x ∓ 16 = 0.
The length of latus-rectum is given as: 2a2/b = 2(9)/4 = 9/2.
(iii) 4x2 – 3y2 = 36
Solution:
Given: 4x2 – 3y2 = 36
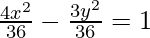

This is of the form 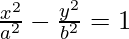 where, a2 = 9, b2 = 12 i.e., a = 3 and b = √12
where, a2 = 9, b2 = 12 i.e., a = 3 and b = √12
Eccentricity is given by:
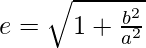
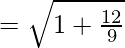
Eccentricity = 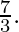
Foci: The coordinates of the foci are (±ae, 0)= (±ae, 0) = (±√21, 0)
The length of latus-rectum is given as= 2b2/a = 2(12)/3 = 24/3 = 8
(iv) 3x2 – y2 = 4
Solution:
Given: 3x2 – y2 = 4
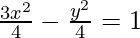
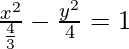
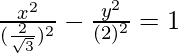
This is of the form 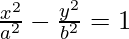 where,
where, 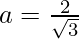 and b = 2
and b = 2
Eccentricity is given by:
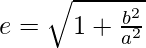
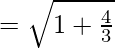
Eccentricity = 2
Foci: The coordinates of the foci are (±ae, 0)= (±ae, 0) = ±(2/√3)(2) = ±4/√3
(±ae, 0) = (±4/√3, 0)
The length of latus-rectum is given as:= 2b2/a = 2(4)/[2/√3] = 4√3.
(v) 2x2 – 3y2 = 5
Solution:
Given: 2x2 – 3y2 = 5
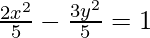
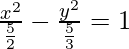
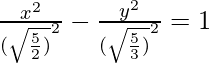
This is of the form 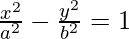 where,
where, 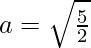 and
and 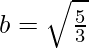
Eccentricity is given by:
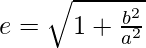
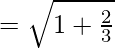
Eccentricity = 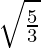 .
.
Foci: The coordinates of the foci are (±ae, 0)
or, (±ae, 0) = 
The length of latus-rectum is given as: 2b2/a = 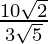
Question 4. Find the axes, eccentricity, latus-rectum, and the coordinates of the foci of the hyperbola 25x2 – 36y2 = 225.
Solution:
Given: 25x2 – 36y2 = 225
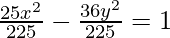
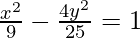
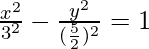
This is of the form 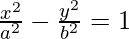 where, a = 3 and b = 5/2
where, a = 3 and b = 5/2
Eccentricity is given by:
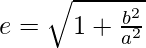
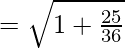
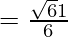
Foci: The coordinates of the foci are (±ae, 0)
(±ae, 0) = (± √61/2, 0)
The length of latus-rectum is given as: 2b2/a
∴ Transverse axis = 6, conjugate axis = 5, e = √61/6, LR = 25/6, foci = (± √61/2, 0)
Question 5. Find the center, eccentricity, foci, and directions of the hyperbola
(i) 16x2 – 9y2 + 32x + 36y – 164 = 0
Solution:
Given: 16x2 – 9y2 + 32x + 36y – 164 = 0.
⇒ 16x2 + 32x + 16 – 9y2 + 36y – 36 – 16 + 36 – 164 = 0
⇒ 16(x2 + 2x + 1) – 9(y2 – 4y + 4) – 16 + 36 – 164 = 0
⇒ 16(x2 + 2x + 1) – 9(y2 – 4y + 4) – 144 = 0
⇒ 16(x + 1)2 – 9(y – 2)2 = 144
Here, center of the hyperbola is (-1, 2).
So, let x + 1 = X and y – 2 = Y
The obtained equation is of the form 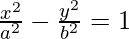 where, a = 3 and b = 4.
where, a = 3 and b = 4.
Eccentricity is given by:
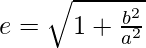
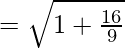
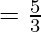
Foci: The coordinates of the foci are (±ae, 0)
X = ±5 and Y = 0
x + 1 = ±5 and y – 2 = 0
x = ±5 – 1 and y = 2
x = 4, -6 and y = 2
So, Foci: (4, 2) (-6, 2)
∴ The center is (-1, 2), eccentricity (e) = 5/3, Foci = (4, 2) (-6, 2), Equation of directrix = 5x – 4 = 0 and 5x + 14 = 0.
(ii) x2 – y2 + 4x = 0
Solution:
Given: x2 – y2 + 4x = 0.
⇒ x2 – y2 + 4x = 0
⇒ x2 + 4x + 4 – y2 – 4 = 0
⇒ (x + 2)2 – y2 = 4
Here, center of the hyperbola is (2, 0).
The obtained equation is of the form 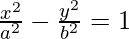 where, a = 2 and b = 2
where, a = 2 and b = 2
Eccentricity is given by:
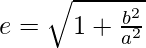
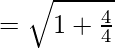
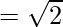
Foci: The coordinates of the foci are (±ae, 0)
X = ± 2√2 and Y = 0
X + 2 = ± 2√2 and Y = 0
X= ± 2√2 – 2 and Y = 0
So, Foci = (± 2√2 – 2, 0)
∴ The center is (-2, 0), eccentricity (e) = √2, Foci = (-2± 2√2, 0), Equation of directrix = x + 2 = ±√2.
(iii) x2 – 3y2 – 2x = 8
Solution:
Given: x2 – 3y2 – 2x = 8.
⇒ x2 – 3y2 – 2x = 8
⇒ x2 – 2x + 1 – 3y2 – 1 = 8
⇒ (x – 1)2 – 3y2 = 9
Here, center of the hyperbola is (1, 0)
The obtained equation is of the form 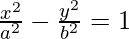 where, a = 3 and b = √3
where, a = 3 and b = √3
Eccentricity is given by:
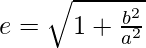
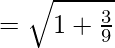

Foci: The coordinates of the foci are (±ae, 0)
X = ± 2√3 and Y = 0
X – 1 = ± 2√3 and Y = 0
X= ± 2√3 + 1 and Y = 0
So, Foci = (1 ± 2√3, 0)
∴ The center is (1, 0), eccentricity (e) = 2√3/3, Foci = (1 ± 2√3, 0), Equation of directrix = X = 1±9/2√3.
Question 6. Find the equation of the hyperbola, referred to its principal axes as axes of coordinates, in the following cases:
(i) the distance between the foci = 16 and eccentricity = √2
Solution:
Given: Distance between the foci = 16 and Eccentricity = √2
Let us compare with the equation of the form 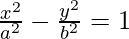 …..(1)
…..(1)
Distance between the foci is 2ae and b2 = a2(e2 – 1)
So, 2ae = 16
⇒ ae = 16/2
⇒ a√2 = 8
⇒ a = 8/√2
⇒ a2 = 64/2 = 32
We know that, b2 = a2(e2 – 1)
So, b2 = 32[(√2)2 – 1]
= 32(2 – 1)
= 32
The Equation of hyperbola is given as 
⇒ x2 – y2 = 32
∴ The Equation of hyperbola is x2 – y2 = 32.
(ii) conjugate axis is 5 and the distance between foci = 13
Solution:
Given: Conjugate axis = 5 and Distance between foci = 13
Let us compare with the equation of the form 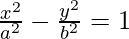 …..(1)
…..(1)
Distance between the foci is 2ae and b2 = a2(e2 – 1)
Length of conjugate axis is 2b
So, 2b = 5
⇒ b = 5/2
⇒ b2 = 25/4
We know that, 2ae = 13
ae = 13/2
⇒ a2e2 = 169/4
b2 = a2(e2 – 1)
⇒ b2 = a2e2 – a2
⇒ 25/4 = 169/4 – a2
⇒ a2 = 169/4 – 25/4
⇒ a2 = 144/4 = 36
The Equation of hyperbola is given as 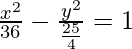
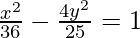
∴ The Equation of hyperbola is 25x2 – 144y2 = 900.
(iii) conjugate axis is 7 and passes through the point (3, -2)
Solution:
Given: Conjugate axis = 7 and Passes through the point (3, -2)
Conjugate axis is 2b
So, 2b = 7
⇒ b = 7/2
⇒ b2 = 49/4
The Equation of hyperbola is given as 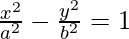
Since it passes through points (3, -2), we have
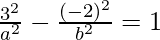
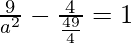
⇒ a2 = 441/65
The equation of hyperbola is given as: 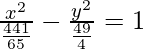
∴ The Equation of hyperbola is 65x2 – 36y2 = 441.
Question 7. Find the equation of the hyperbola whose:
(i) foci are (6,4) and (-4,4) and eccentricity is 2.
Solution:
Clearly, coordinates of the center are (1,4).
Equation of the hyperbola is:
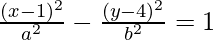
Distance between the foci = 2ae
⇒ 2ae = 10
⇒ a = 5/2
⇒ a2 = 25/4
Since, b2 = a2(e2 – 1)
⇒ b2 = 75/4
Putting the values in the equation, we get
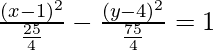
⇒ 12×2 – 4y2 – 24x + 32y -127 = 0.
(ii) vertices are (-8,-1) and (16,-1) and focus is (17,-1)
Solution:
Clearly, coordinates of the center are (4,-1).
Equation of the hyperbola is :
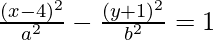
Distance between vertices = 2ae
⇒ 24 = 2a
⇒ a = 12
⇒ a2 = 144 and e2 = 169/144
Since, b2 = a2(e2 – 1)
⇒ b2 = 25
Putting the values in the equation, we get

⇒ 25x2 – 144y2 – 200x – 288y – 3344 = 0.
(iii) foci are (4, 2) and (8, 2) and eccentricity is 2.
Solution:
Clearly, coordinates of the center are (6, 2).
Equation of the hyperbola is:
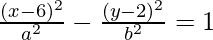
Distance between the foci = 2ae
⇒ 2ae = 4
⇒ a = 1
Since, b2 = a2(e2 – 1)
⇒ b2 =3
Putting the values in the equation, we get
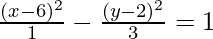
⇒ 3×2 – y2 – 36x + 4y + 101 = 0.
(iv) vertices are (0, ±7) and foci at (0, ±28/3).
Solution:
Vertices of coordinates are (0, ±b) and (0, ±be).
⇒ b = 7
⇒ b2 = 49
and, be = 28/3
⇒ e = 4/3 ⇒ e2 = 16/9
Now, a2 = b2(e2-1)
⇒ a2 = 343/9
The equation becomes:
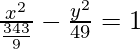
(v) vertices are at (±6, 0) and one of the directrices is x = 4.
Solution:
It is given that the vertices of the hyperbola are (±6, 0).
=> a = 6
=> a2 = 36
Now, x = 4
=> a/e = 4
=> 6/e = 4
=> e = 3/2
Now we know,
(ae)2 = a2 + b2
(6 × (3/2))2 = 62 + b2
b2 = 81 – 36
b2 = 45
The equation becomes,
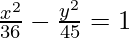
(vi) Whose foci are at (± 2, 0) and eccentricity is 3/2.
Solution:
We have the foci given as, (± 2, 0).
Here e = 3/2. We know,
ae = 2
=> a = 2/e
=> a = 2/(3/2)
=> a = 4/3
Now we know,
(ae)2 = a2 + b2
(2)2 = (4/3)2 + b2
b2 = 4 – 16/3
b2 = 20/9
So the equation becomes,,
=> 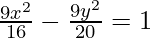
=> 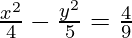
Question 8. Find the eccentricity if the length of the conjugate axis is 3/4 of the length of the traverse axis.
Solution:
Given: 2b = 6a/4
⇒ b/a = 3/4
⇒ b2/a2 = 9/16
Now, 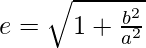

e = 5/4.
Question 9. Find the equation of the hyperbola whose focus is at (5,2) and (4,2) and center at (3,2).
Solution:
Clearly the coordinates of the first vertex are (2,2).
Equation of the hyperbola is :

Distance between 2 vertices = 2a
⇒ a = 1
and, e = 2
b2 = a2(e2 – 1)
⇒ b2 = 3
The equation becomes:
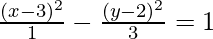
⇒ 3(x-3)2 – (y-2)2 = 3.
Question 10. If P is any point on the hyperbola whose axis is equal, prove that SP.S’P = CP2.
Solution:
Given: a = b
Equation becomes: x2 – y2 = a2
 , C = (0,0),
, C = (0,0), 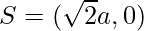 and
and 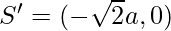
SP. S’P = 4a4 + 4a2(a2 + b2) + (a2 + b2)2 – 8a2b2
= (a2 + b2)2 = CP
Hence, SP.S’P = CP2.
Question 11. Find the equation of the hyperbola whose:
(i) foci are (±2,0) and foci are (±3,0).
Solution:
Equation of the hyperbola is :
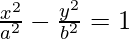
Distance between the foci = 2ae
⇒ a = 2
⇒ a2 = 4
e = 3/2
Since, b2 = a2(e2 – 1)
⇒ b2 = 5
Putting the values in the equation, we get
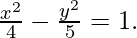
(ii) vertices are (0, ±4) and foci at (0, ±2/3).
Solution:
Vertices of coordinates are (0, ±b) and (0, ±be).
⇒ b = 4
⇒ b2 = 16
and, be = 2/3
⇒ e = 2/3 ⇒ e2 = 4/9
Now, a2 = b2(e2-1)
⇒ a2 = 343/9
The equation becomes:
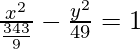
Question 12. Find the equation when the distance between foci is 16 and eccentricity is 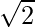 .
.
Solution:
Distance between foci = 2ae = 16
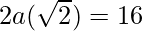
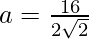
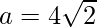

or, b2 = 32
Equation becomes: x2 – y2 = 32.
Question 13. Show that the set of all points such that the difference of their distance from (4,0) and (-4,0) is always equal to 2 represents a hyperbola.
Solution:
Let P(x, y) be the point of the set.
Distance of P from (4,0) = 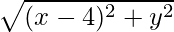
Distance of P from (-4,0) = 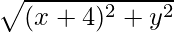
Given:

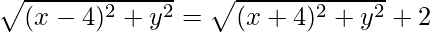
Squaring both sides, we have
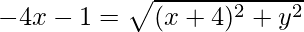
⇒ 15x2 – y2 = 15.
Thus, P represents a hyperbola.
Share your thoughts in the comments
Please Login to comment...