Question 1(i). Find the coordinates of the centre and radius of the circle x2 + y2 + 6x – 8y – 24 = 0.
Solution:
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Centre = (-g, -f)
Radius = 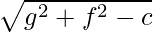
Given equation of circle is x2 + y2 + 6x – 8y – 24 = 0
On comparing with eq(i), we get
Hence, g = 3, f = -4, c = -24
So,
Centre = (-3, 4)
Radius = 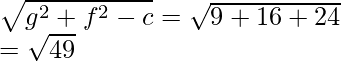
Radius = 7
Question 1(ii). Find the coordinates of the centre and radius of the circle 2x2 + 2y2 – 3x + 5y = 7.
Solution:
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Centre = (-g, -f)
Radius = 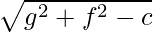
Given equation of circle is 2x2 + 2y2 – 3x + 5y – 7 = 0
x2 + y2 – 3/2x + 5/2y – 7/2 = 0
On comparing with eq(i), we get
Hence, g = -3/4, f = 5/4, c = -7/2
So, center = (3/4, -5/4)
Radius = 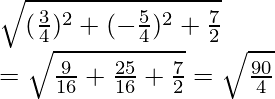
Radius = 3√10/4
Question 1(iii). Find the coordinates of the centre and radius of the circle 1/2(x2 + y2) + x cosθ + y sinθ – 4 = 0.
Solution:
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Centre = (-g, -f)
Radius = 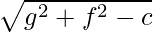
Given equation of circle is 1/2(x2 + y2) + x cosθ + y sinθ – 4 = 0
⇒ x2 + y2 + 2x cosθ + 2sin θ – 8 = 0
On comparing with eq(i), we get
Hence, g = cos θ, f = sin θ, c = -8
So, centre = (-cos θ, -sinθ)
Radius = 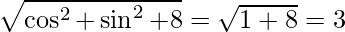
Radius = 3
Question 1(iv). Find the coordinates of the centre and radius of the circle x2 + y2 – ax – by = 0.
Solution:
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Centre = (-g, -f)
Radius = 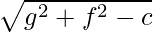
Given equation of circle is x2 + y2 – ax – by = 0
On comparing with eq(i), we get
Hence, g = -a/2, f = -b/2, c = 0
So, centre = (a/2, b/2)
Radius = 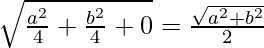
Radius = 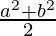
Question 2(i). Find the equation of the circle passing through the points (5, 7), (8, 1), and (1, 3).
Solution:
Given that, the circle pass through points P(5, 7), Q(8, 1), and R(1, 3)
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Since, P, Q, and R lies on eq(i)
So,
25 + 49 + 10g + 14f + c = 0 …….(ii)
64 + 1 + 16g + 2f + c = 0 …….(iii)
1 + 9 + 2g + 6f + c = 0 ……(iv)
Now on solving eq (ii), (iii), and (iv), we get,
g = -29/6, f = -19/6, c = 56/3
Now put all these values in eq(i), we get
The equation of circle is
x2 + y2 – 29/3x – 19/6y + 56/3 = 0
3(x2 + y2) – 29x – 19y + 56 = 0
Question 2(ii). Find the equation of the circle passing through the points (1, 2), (3, -4), and (5, -6).
Solution:
Given that, the circle pass through points P(1, 2), Q(3, -4), and R(5, -6)
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Since, P, Q, and R lies on eq(i)
So,
1 + 4 + 2g + 4f + c = 0 …..(ii)
9 + 16 + 6g – 8f + c = 0 …..(iii)
25 + 36 + 10g – 12f + c = 0 …..(iv)
Now on solving eq (ii), (iii), and (iv), we get,
g = -11, f = -2, and c = 25
Now put all these values in eq(i), we get
The equation of circle is
x2 + y2 – 22x – 4y + 25 = 0
Question 2(iii). Find the equation of the circle passing through the points (5, -8), (-2, 9), and (2, 1).
Solution:
Given that, the circle pass through points P(5, -8), Q(-2, 9), and R(2, 1)
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Since, P, Q, and R lies on eq(i)
So,
25 + 64 + 10g – 16f + c = 0 …..(ii)
4 + 81 – 4g + 18f + c = 0 …..(iii)
4 + 1 + 4g + 2f + c = 0 …..(iv)
Now on solving eq (ii), (iii), and (iv), we get,
g = 58, f = 24, and c = -285
Now put all these values in eq(i), we get
The equation of circle is
x2 + y2 + 116x + 48y – 285 = 0
Question 2(iv). Find the equation of the circle passing through the points (0, 0), (-2, 1), and (-3, 2).
Given that, the circle pass through points P(0, 0), Q(-2, 1), and R(-3, 2)
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Since, P, Q, and R lies on eq(i)
So,
0 + 00 + 0 + c = 0 …..(ii)
4 + 1 – 4x + 2y + c = 0 …..(iii)
9 + 4 – 6x + 4y + c = 0 …..(iv)
Now on solving eq (ii), (iii), and (iv), we get,
g = -3/2, f = -11/2, and c = 0
Now put all these values in eq(i), we get
The equation of circle is
x2 + y2 – 3x – 11y = 0
Question 3. Find the equation of the circle which passes through (3, -2), (-2, 0) and has its centre on the line 2x – y = 3.
Solution:
It is given that, the circle passing through P(3, -2) and Q(-2, 0) and having its centre on 2x – y = 3.
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Since the circle passes through (3, -2) and also (-2, 0)
So,
9 + 4 + 6g – 4f + c = 0 …..(ii)
4 + 0 – 4g + 0 + c = 0 …..(iii)
Also, the centre of the circle lies on 2x – y = 3
-2g + f = 3 …..(iv)
Now on solving eq (ii), (iii), and (iv), we get,
g = 3/2, f = 6, and c = 2
Now put all these values in eq(i), we get
The equation of circle is
x2 + y2 + 3x + 12y + 2 = 0
Question 4. Find the equation of the circle which passes through points (3, 7), (5, 5), and has its centre on the line x – 4y = 1.
Solution:
It is given that, the circle passing through P(3, 7) and Q(5, 5) and having its centre on x – 4y = 1
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Since the circle passes through P and Q
so,
9 + 49 + 7g + 14f + c = 0 …..(ii)
25 + 25 + 10g + 10f + c = 0 …..(iii)
Also, the centre of the circle lies on x – 4y = 1
so, -g + 4f = 1 …..(iv)
Now on solving eq (ii), (iii), and (iv), we get,
g = 3, f = 1, and c = -90
Now put all these values in eq(i), we get
The equation of circle is
x2 + y2+ 6x + 2y – 90 = 0
Question 5. Show that the points (3, -2), (1, 0), (-1, -2) and (1, -4) are concyclic.
Solution:
Given that P (3, -2), Q(1, 0), R(-1, -2), and S(1,-4)
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Since the circle passes through P, Q and R
So,
9 + 4 + 6g – 4f + c = 0 …..(ii)
1 + 0 + 2g – 0 + c = 0 …..(iii)
1 + 4 – 2g – 4f + c = 0 …..(iv)
Now on solving eq (ii), (iii), and (iv), we get,
g = -1, f = 2 and c = 1
Now put all these values in eq(i), we get
The equation of circle is
x2 + y2 – 2x + 4y + 1 = 0 …..(v)
Here, we clearly see that point S(1,-4) satisfy eq(v)
Hence, points P, Q, R, and S are concyclic
Question 6. Show that the point (5, 5), (6, 4), (-2, 4), and (7, 1) all lie on a circle, and find its equation, centre, and radius.
Solution:
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Centre = (-g, -f)
Radius = 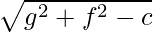
Therefore, P(5, 5), Q(6, 4), and R(-2, 4) lie on eq(i),
So,
25 + 25 + 10g + 10f + c = 0 …..(ii)
36 + 16 + 12g + 8f + c = 0 …..(iii)
4 + 16 + 4g + 8f + c = 0 …..(iv)
Now on solving eq (ii), (iii), and (iv), we get,
g = -2, f = -1, c = -20
Now put all these values in eq(i), we get
The equation of circle is
x2 + y2 – 4x – 2y – 20 = 0 …..(v)
Here, we clearly see that point S(7, 1)
Hence, points P, Q, R, and S are concyclic
Now, the centre = (-g, -f) = (2, 1)
Radius = 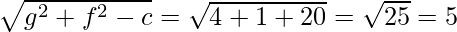
Question 7(i). Find the equation of the circle which circumscribes the triangle formed by the lines x + y + 3 = 0, x – y + 1 = 0, and x = 3.
Solution:
The equations of lines are
x + y = -3 …..(i)
x – y = -1 …..(ii)
x = 3 …..(iii)
Let us considered A, B, and C are the point of intersection of lines (i), (ii), and (iii)
So, Point A(-2,-1), B(3, 4), and C(3,-6)
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(iv)
So, the circle circumscribing the ∆ABC
4 + 1 – 4g – 2f + c = 0 …..(v)
9 + 16 + 6g + Bf + c = 0 …..(vi)
9 + 36 + 6g – 12f + c = 0 …..(vii)
Now on solving eq (v), (vi), and (vii), we get,
g = -3, f = 1, c = -15
Now put all these values in eq(iv), we get
The equation of circle is
x2 + y2 – 6x + 2y – 15 = 0
Question 7(ii). Find the equation of the circle which circumscribes the triangle formed by the lines 2x + y – 3 = 0, x + y – 1 = 0, and 3x + 2y – 5 = 0.
Solution:
The equations of lines are
2x + y = 3 …..(i)
x + y = 1 …..(ii)
3x + 3y = 5 …..(iii)
Let us considered A, B, and C are the point of intersection of lines (i), (ii), and (iii)
So, A = (2, -1)
B = (3, -2)
C = (1, 1)
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(iv)
So, the circle circumscribing the ∆ABC
4 + 1 + 4g – 2f + c = 0 …..(v)
9 + 4 + 6g – 4f + c = 0 …..(vi)
1 + 1 + 2g + 2f + c = 0 …..(vii)
Now on solving eq (v), (vi), and (vii), we get,
g = -13/2, f = -5/2, and c = 16
Now put all these values in eq(iv), we get
The equation of circle is
x2 + y2 – 13x – 5y + 16 = 0
Question 7(iii). Find the equation of the circle which circumscribes the triangle formed by the lines x + y = 2, 3x – 4y = 6, and x – y = 0.
Solution:
The equations of lines are
x + y = 2 …..(i)
3x – 4y = 6 …..(ii)
x – y = 0 …..(iii)
Let us considered A, B, and C are the point of intersection of lines (i), (ii), and (iii)
So, A = (2, 0)
B = (-6, -6)
C = (1, 1)
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(iv)
So, the circle circumscribing the ∆ABC
4 + 4g + c = 0 …..(v)
36 + 36 – 12g – 12f + c = 0 …..(vi)
1 + 1 + 2g + 2f + c = 0 …..(vii)
Now on solving eq (v), (vi), and (vii), we get,
g = 2, f = 3, and c = -12
Now put all these values in eq(iv), we get
The equation of circle is
x2 + y2 + 4x + 6y – 12 = 0
Question 7(iv). Find the equation of the circle which circumscribes the triangle formed by the lines y = x + 2, 3y = 4x, and 2y = 3x.
Solution:
The equations of lines are
y = x + 2 …..(i)
3y = 4x …..(ii)
2y = 3x …..(iii)
Let us considered A, B, and C are the point of intersection of lines (i), (ii), and (iii)
So, A = (6, 8)
B = (4, 6)
C = (0, 0)
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(iv)
So, the circle circumscribing the ∆ABC
12g + 16f + c = -100 …..(v)
8g + 12f + c = -52 …..(vi)
c = 0 …..(vii)
Now on solving eq (v), (vi), and (vii), we get,
f = 11 and g = -23
Now put all these values in eq(iv), we get
The equation of circle is
x2 + y2 – 46x + 22y = 0.
Question 8. Prove that the centre of the three circles x2 + y2 – 4x – 6y – 12 = 0, x2 + y2 + 2x + 4y – 10 = 0, and x2 + y2 -10x – 16y – 1 = 0 are collinear.
Solution:
The given equation of circles are,
x2 + y2 – 4x – 6y – 12 = 0 …….(i)
x2 + y2 + 2x + 4y – 10 = 0 …….(ii)
x2 + y2 – 10x – 16y – 1 = 0 …….(iii)
Let O1, O2 and O3 are the centres of (i), (ii), and (iii)
O1 = (-g, -f) = (2, 3)
O2 = (-g, -f) = (-1, -2)
O3 = (-g, -f) = (5, 8)
O1, O2 and O3 will be collinear if ar(∆ O1O2O3) = 0
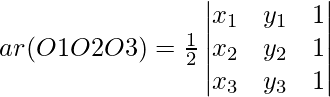
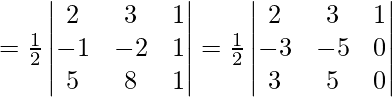
R2 ⇒ R2 ⇒ -R1
R3 ⇒ R3 ⇒ -R1
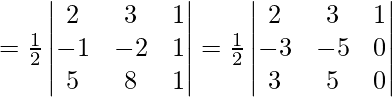
O1, O2, and O3 are collinear
Question 9. Prove that the radii of the circles x2 + y2 = 1, x2 + y2 – 2x – 6y – 6 = 0, and x2 + y2 – 4x – 12y – 9 = 0 are in A.P.
Solution:
The given equation of circles are,
x2 + y2 = 1 ———–(i)
x2 + y2 – 2x – 6y – 6 = 0 ———-(ii)
x2 + y2 – 4x – 12y – 9 = 0 ———-(iii)
Let us considered R1, R2, and R3 are the radii of (i), (ii), and (iii)
So, R1 = 1
R2 = 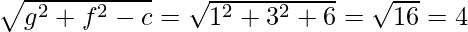
R3 = 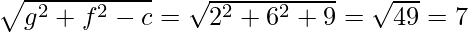
As we know that if a, b, c are in AP, then b = a + b/2
so, a = 1, b = 4, c = 7, b = 1 + 7/2 = 4
Therefore 1, 4, 7 are in AP.
Hence, the radius of the three circles lie in AP.
Question 10. Find the equation of the circle which passes through the origin and cuts off chord of length 4 and 6 on the positive side of the x-axis and y-axis respectively.
Solution:
It is given that a circle that passes through origin O(0, 0) and
cut off on intercepts of length 4 on x-axis and 6 on y-axis.
So, OA = 4
OB = 6
Let us assume C be the centre of the circle and
CM and CN are perpendicular line drawn on OA and OB
so, the coordinate of A = (4, 0) and B = (0, 6)
The coordinates of M = (2, 0) and N = (0, 3)
And the coordinates of C = (2, 3)
Now in ∆OCM,
Using Pythagoras theorem
OC2 = OM2 + CM2
= 22 + 32
= 4 + 9
OC = √13
Hence, the required circle is
(x – 2)2 + (y – 3)2 = 13
x2 + y2 – 4x – 6y = 0
Question 11. Find the equation of the circle concentric with circles x2 + y2 – 6x + 12y + 15 = 0 and double of its area.
Solution:
The given equation of circle is
x2 + y2 – 6x + 12y + 15 = 0 …….(i)
so, centre = (-g, -f) = (3, 6)
radius = 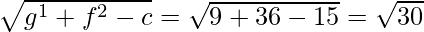
Now, the required equation of circle in concentric with (i)
that means both have same centre (3,-6)
The area of required circle = 2 * Area of (i)
πR2 = 2 * π(√30)2
R2 = 60
R = 2√15
Hence, the required circle is
(x – 3)2 + (y + 6)2 = 60
x2 + y2 – 6x + 12y – 15 = 0
Question 12. Find the equation of the circle which passes through the points (1, 1), (2, 2), and whose radius is 1. Show that there are two such circles.
Solution:
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
It is given that the points P(1, 1) and Q(2, 2) passes through it eq(1)
So,
1 + 1 + 2g + 2f + c = 0 …..(ii)
4 + 4 + 4g + 4f + c = 0 …..(iii)
It is given that the radius = 1
⇒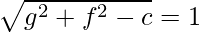
⇒ g2 + f2 – c = 1 ……(iv)
Now from eq(ii) and (iii), we get
g + f + c/2 = -1
g + f + c/4 = -2
Now on subtracting both the equations, we get
c = 4
g + f = -3 …….(v)
Now on solving eq(v) and (vi), we get
g = -1 or -2 and f = -2 or -1
Hence, the required circle is
x2 + y2 – 2x – 4y + 4 = 0
or
x2 + y2 – 4x – 2y + 4 = 0
Question 13. Find the equation of the circle concentric with x2 + y2 – 4x – 6x – 6y – 3 = 0 and which touches the y-axis.
Solution:
The given equation of circle is
x2 + y2 – 4x – 6y – 3 = 0 …..(i)
so, centre = (-g, -f) = (2, 3)
The required circle is concentric with eq(i)
so, both have centre(2, 3)
Also, the required circle touches y-axis at A.
So, CA = radius = 2
Hence, the required circle is
(x – 2)2 + (y – 3)2 = 4
x2 + y2 – 4x – 6y + 9 = 0
Question 14. If a circle passes through the point (0, 0), (a, 0), (0, b), then find the coordinates of its centre.
Solution:
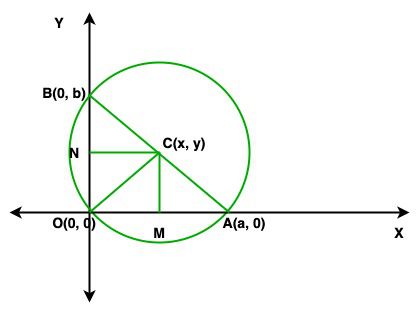
From the given figure, CA, CO, and AB are the equal radii of the circle
So,
CA = CO = CB = r
Also, OCA is an isosceles triangle, and CM is the perpendicular bisector to the OA.
Hence OM = a/2
Similarly, CN is the perpendicular bisector to the OB
So, ON = b/2
from the above figure, it is clear that
OM = x = a/2
ON = y = b/2
Hence the centre of the circle is c(a/2, b/2)
Question 15. Find the equation of the circle which passes through the point (2, 3) and (4, 5), and the centre lies on the straight line y – 4x + 3 = 0.
Solution:
It is given that a circle which passes through the point P(2, 3) and Q(4, 5) and
the centre lies on the straight line y – 4x + 3 = 0.
As we know that the general equation of circles is
x2 + y2 + 2gx + 2fy + c = 0 …..(i)
Since the circle passes through P, and Q
So,
13 + 14g + 6f + c = 0 …..(ii)
41 + 8g + 10f + c = 0 …..(iii)
Centre (-g, -f) lies on y – 4x + 3 = 0
So, -f + 4g = -3 …..(iv)
Now on subtracting eq(ii) from (iii), we get
28 + 4g + 4f = 0 …..(v)
On solving eq(iv) and (v) we get,
f = -5 and g = -2
Now put all these values in eq(i), we get
The equation of circle is
41 – 16 – 50 + c = 0
c = 25
Hence, the required equation of the circle is,
x2 + y2 – 4x – 10y + 25 = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...