Class 11 RD Sharma Solutions- Chapter 23 The Straight Lines- Exercise 23.17
Last Updated :
19 Jan, 2021
Question 1. Prove that the area of the parallelogram formed by the lines
a1x + b1y + c1 = 0, a1x + b1y + d1 = 0, a2x + b2y + c2 = 0, a2x + b2y + d2 = 0 is 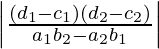 sq. units.
sq. units.
Deduce the condition for these lines to form a rhombus.
Solution:
Given:
The given lines are
a1x + b1y + c1 = 0 —(equation-1)
a1x + b1y + d1 = 0 —(equation-2)
a2x + b2y + c2 = 0 —(equation-3)
a2x + b2y + d2 = 0 —(equation-4)
Let us prove, the area of the parallelogram formed by the lines a1x + b1y + c1 = 0, a1x + b1y + d1 = 0, a2x + b2y + c2 = 0, a2x + b2y + d2 = 0 is
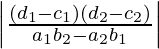 sq. units.
sq. units.
The area of the parallelogram formed by the lines a1x + b1y + c1 = 0, a1x + b1y + d1 = 0, a2x + b2y + c2 = 0 and a2x + b2y + d2 = 0 is given below:
Area = 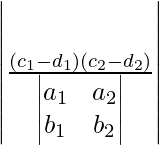
Since, \begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix} = a1b2 – a2b1
Therefore, Area = 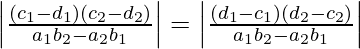
If the given parallelogram is a rhombus, then the distance between the pair of parallel lines is equal.
Therefore, 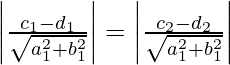
Hence proved.
Question 2. Prove that the area of the parallelogram formed by the lines 3x – 4y + a = 0, 3x – 4y + 3a = 0, 4x – 3y – a = 0 and 4x – 3y – 2a = 0 is 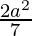 sq. units.
sq. units.
Solution:
Given:
The given lines are
3x − 4y + a = 0 —(equation-1)
3x − 4y + 3a = 0 —(equation-2)
4x − 3y − a = 0 —(equation-3)
4x − 3y − 2a = 0 —(equation-4)
We have to prove, the area of the parallelogram formed by the lines 3x – 4y + a = 0, 3x – 4y + 3a = 0, 4x – 3y – a = 0 and 4x – 3y – 2a = 0 is 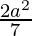 sq. units.
sq. units.
From above solution, we know that
Area of the parallelogram = 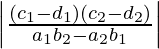
Area of the parallelogram = 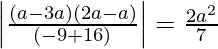 sq. units
sq. units
Hence proved.
Question 3. Show that the diagonals of the parallelogram whose sides are lx + my + n = 0, lx + my + n’ = 0, mx + ly + n = 0 and mx + ly + n’ = 0 include an angle π/2.
Solution:
Given:
The given lines are
lx + my + n = 0 —(equation-1)
mx + ly + n’ = 0 —(equation-2)
lx + my + n’ = 0 —(equation-3)
mx + ly + n = 0 —(equation-4)
We have to prove, the diagonals of the parallelogram whose sides are lx + my + n = 0, lx + my + n’ = 0, mx + ly + n = 0 and mx + ly + n’ = 0 include an angle 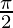 .
.
By solving equation (1) and (2), we will get
B = 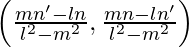
Solving equation (2) and (3), we get
C = 
Solving equation (3) and (4), we get
D = 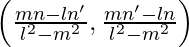
Solving equation (1) and (4), we get
A = 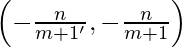
Let m1 and m2 be the slope of AC and BD.
Now,
m1 = 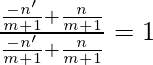
m2 = 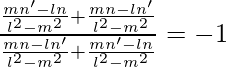
Therefore,
m1m2 = -1
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...