Class 11 RD Sharma Solutions- Chapter 23 The Straight Lines- Exercise 23.16
Last Updated :
19 Jan, 2021
Question 1. Determine the distance between the following pair of parallel lines:
(i) 4x – 3y – 9 = 0 and 4x – 3y – 24 = 0
(ii) 8x + 15y – 34 = 0 and 8x + 15y + 31 = 0
(iii) y = mx + c and y = mx + d
(iv) 4x + 3y – 11 = 0 and 8x + 6y = 15
Solution:
(i) 4x – 3y – 9 = 0 and 4x – 3y – 24 = 0
Given:
The parallel lines are
4x − 3y − 9 = 0 —(Equation-1)
4x − 3y − 24 = 0 —(Equation-2)
Let ‘d’ be the distance between the given lines.
Thus,
d = 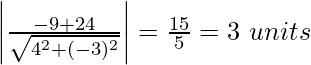
Therefore,
The distance between givens parallel line is 3 units.
(ii) 8x + 15y – 34 = 0 and 8x + 15y + 31 = 0
Given:
The parallel lines are
8x + 15y − 34 = 0 —(Equation-1)
8x + 15y + 31 = 0 —(Equation-2)
Let ‘d’ be the distance between the given lines.
Thus,
d = 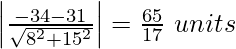
Therefore,
The distance between givens parallel line is 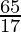 units.
units.
(iii) y = mx + c and y = mx + d
Distance between y = mx + c and y = mx + d is
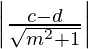
(iv) 4x + 3y – 11 = 0 and 8x + 6y = 15
The distance between 4x + 3y – 11 = 0 and 8x + 6y = 15 is
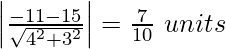
Question 2. The equations of two sides of a square are 5x – 12y – 65 = 0 and 5x – 12y + 26 = 0. Find the area of the square.
Solution:
Given:
Two side of square are 5x – 12y – 65 = 0 and 5x – 12y + 26 = 0
The sides of a square are
5x − 12y − 65 = 0 —(Equation-1)
5x − 12y + 26 = 0 —(Equation-2)
Here we can see that lines (1) and (2) are parallel.
Hence, the distance between them will give the length of the side of the square.
Let ‘d’ be the distance between the given lines.
d = 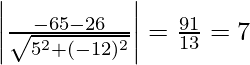
Therefore,
Area of the square = 72 = 49 square units
Question 3. Find the equation of two straight lines that are parallel to x + 7y + 2 = 0 and at unit distance from the point (1, -1).
Solution:
Given:
The equation is parallel to x + 7y + 2 = 0 and at unit distance from the point (1, -1)
The equation of given line is
x + 7y + 2 = 0 —(Equation-1)
The equation of a line parallel to line x + 7y + 2 = 0 is given below:
x + 7y + λ = 0 —(Equation-2)
The line x + 7y + λ = 0 is at a unit distance from the point (1, − 1).
Thus,
1 = 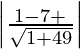
λ – 6 = ± 5√2
λ = 6 + 5√2, 6 – 5√2
Now,
Substitute the value of λ back in equation x + 7y + λ = 0, we get
x + 7y + 6 + 5√2 = 0 and x + 7y + 6 – 5√2
Therefore, The required lines:
x + 7y + 6 + 5√2 = 0 and x + 7y + 6 – 5√2
Question 4. Prove that the lines 2x + 3y = 19 and 2x + 3y + 7 = 0 are equidistant from the line 2x + 3y = 6.
Solution:
Given:
The lines A, 2x + 3y = 19 and B, 2x + 3y + 7 = 0 also a line C, 2x + 3y = 6.
Let d1 be the distance between lines 2x + 3y = 19 and 2x + 3y = 6,
While d2 is the distance between lines 2x + 3y + 7 = 0 and 2x + 3y = 6
d1 =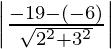 and d2 =
and d2 = 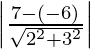
d1 = 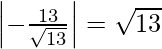 and d2 =
and d2 = 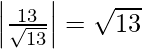
Hence, proved, the lines 2x + 3y = 19 and 2x + 3y + 7 = 0 are equidistant from the line 2x + 3y = 6
Question 5. Find the equation of the line mid-way between the parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
Solution:
Given:
9x + 6y – 7 = 0 and 3x + 2y + 6 = 0 are parallel lines
The given equations of the lines are shown as:
3x + 2y – 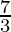 = 0 —(Equation-1)
= 0 —(Equation-1)
3x + 2y + 6 = 0 —(Equation-2)
Let the equation of the line midway between the parallel lines (1) and (2) be
3x + 2y + λ = 0 —(Equation-3)
The distance between (1) and (3) and the distance between (2) and (3) are equal.
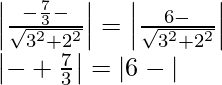
6 – λ = λ + 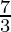
λ = 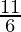
Now substitute the value of λ back in equation 3x + 2y + λ = 0, we get
3x + 2y + 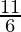 = 0
= 0
By taking LCM
18x + 12y + 11 = 0
Therefore,
The required equation of line is 18x + 12y + 11 = 0.
Question 6. Find the ratio in which the line 3x + 4y + 2 = 0 divides the distance between the lines 3x + 4y + 5 = 0 and 3x + 4y – 5 = 0.
Solution:
Clearly, the slope of each of the given lines is same equal to 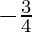
Hence, the line 3x + 4y + 2 = 0 is parallel to each of the given lines.
Putting y = 0 in 3x + 4y + 2 = 0, we get x = 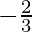
So, the coordinates of a point on 3x + 4y + 2 = 0 are \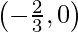
The distance d1 between the lines 3x + 4y + 2 = 0 and 3x + 4y + 5 = 0 is given by
d1 = 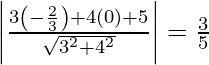
The distance d2 between the lines 3x + 4y + 2 = 0 and 3x + 4y – 5 =0 is given by
d2 = 
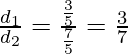
So, 3x + 4y + 2 = 0 divides the distance between the lines 3x + 4y + 5 = 0 and 3x + 4y – 5 = 0 in the ratio 3 : 7.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...