Class 11 RD Sharma Solutions – Chapter 23 The Straight Lines- Exercise 23.12 | Set 3
Last Updated :
01 Nov, 2022
Question 21. Find the coordinates of the foot of the perpendicular from the point (-1, 3) to the line 3x – 4y – 16 = 0.
Solution:
Let us considered the foot of perpendicular of P(-1, 3) on line 3x – 4y = 16 be Q(a, b)
So, (slope of given line) x (slope of PQ) = -1
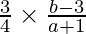
3(b – 3) = -4a – 4
3b – 9 = -4a – 4
4a + 3b = 5 …….(1)
It is given that Q(a, b) lie on the line 3x – 4y = 16
3a – 4b = 16 …….(2)
On solving eq(1) and (2), we get
a = (68/25) and b = (-49/25)
Hence, the coordinate of Q is (68/25, -49/25)
Question 22. Find the projection of the point (1, 0) on the line joining the points (-1, 2) and (5, 4).
Solution:
Let us considered P(-1, 2) and Q(5, 4) are the given point
So, the equation of line PQ is
y – y1 = m(x – x1)

3y – x = 7 ……..(1)
And the slope of line PQ = 1/3
Let us considered point A(1, 0) is the given point and B(x1, y1) be the projection of A
So, the slope of AB = -3
The equation of PQ is
y – 0 = -3(x – 1)
y = -3x + 3 …….(2)
On solving eq(1) and (2), we get
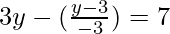
-9y – y + 3 = -21
-10y = -24
y = 12/5
12/5 = -3x + 3
-3x = 12/5 – 3 = (12 -15)/5 = -3/5
x = 1/5
Hence, the B(1/5, 12/5)
Question 23. Find the equation of a line perpendicular to the line √3x – y + 5 = 0 and at a distance of 3 units from the origin.
Solution:
Let us considered the required equation of line is
y – y1 = m'(x – x1) ……….(1)
It is given that the required line is perpendicular to the line √3x – y + 5 = 0
So, the slope of the line is
y = √3x + 5
On comparing y = mx + c, we get
m = √3
m’ = -1/m = -1/√3
and the point is (x1, y1) = (3, 3)
Now put the value of m’ and (x1, y1) is eq(1), we get
y – 3 = -1/√3(x – 3)
x + √3y – 6 = 0
Hence, the required equation of line is x + √3y – 6 = 0
Question 24. The line 2x + 3y = 12 meets the x-axis at A and y-axis at B. The line through (5, 5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
Solution:
It is given that the line 2x+3y=12 meets the x-axis at A and y-axis at B
So, A is 2x = 12 = x = 6
A is (6, 0)
B is 3y = 12
y = 4
B is (0, 4)
It is given that line through (5, 5) perpendicular to 2x + 3y = 12 will have slope = 3/2
y – y1 = m(x – x1)
(y – 5) = 3/2(x – 5)
And 2y – 3x = -5 is equation of line which meets x-axis at C and the line at E
So, C is -3x = -5
x = -5/3
E is (5/3, 0)
Here, E is the point of intersection of two lines
So, 2x + 3y = 12
2y – 3x = -5
Now we find the area of OBCE = area of AOB – area of ACE
= 1/2 x AO x OB – 1/2 x AC x CE
= 24/2 – 1/2 x √13 x 2/3√13
= 24/2 – 1/2 x 2/3 x 13
= 12 – 13/3
= 23/3 sq.unit
Question 25. Find the equation of the straight line which cuts of intercepts on x-axis twice that on y-axis and is at unit distance from the origin.
Solution:
Let us considered the equation of line in intercept form is 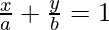
It is given that its intercept on y-axis = 2a
So, the equation is
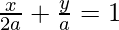
ax + 2ay = 2a2 ……..(1)
Now, perpendicular distance of eq(1) from origin is given unity
So, 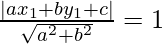
a = a, b = 2a, c = -2a2, x1 = 0, y1 = 0
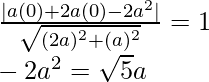
4a4 = a25
a2 = 5/4
a = ±√5/4
So, the intercept form of straight line is
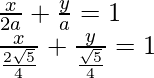
x + 2y = ±√5
Hence, the required equation of line is x + 2y = ±√5
Question 26. The equations of the perpendicular bisector of the sides AB and AC of a triangle ABC x – y + 5 = 0 and x + 2y = 0 respectively. If point A is (1, -2), find the equation of the line BC.
Solution:

Let us considered (x1, y1) and (x2, y2) be the coordinates of B and C.
It is given that perpendicular bisector of AB is x – y + 5 = 0
So, its slope = 1
The coordinates of F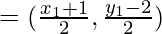
From the figure it is given that F lie on the x – y + 5 = 0
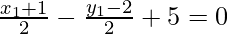
x1 + 1 – y1 + 2 + 10 = 0
x1 – y1 + 13 = 0 ……(1)
From the figure it is given that AB is perpendicular to HF
So, (slope of AB) x (slope of HF) = -1
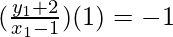
x1 + y1 + 1 = 0
Now on solving equation (1) and (2), we get
x1 = -7, y1 = 6
So, B is (-7, 6)
Now, perpendicular bisector of AC is x + 2y = 0
So, its slope = -1/2
The coordinate of E 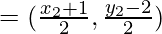
From the figure it is given that E lies on perpendicular bisector of AC
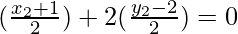
x2 + 1 + 2y2 – 4 = 0
x2 + 2y2 – 3 = 0 ……(3)
Also, AC is perpendicular to HE
So, (slope of AC) x (slope of HE) = -1
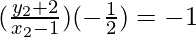
y2 + 2 = 2x2 – 2
2x2 – y2 = 4 …..(4)
On solving equation (3) and (4), we get
x2 = 11/5 , y2 = 2/5
Thus, point C is (11/5, 2/5)
So, the equation of BC is
y – y1=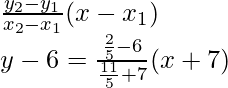
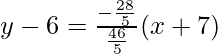
y – 6 = -14/23(x + 7)
23y – 138 = -14x – 98
14x + 23y – 40 = 0
Hence, the required equation of line is 14x + 23y – 40 = 0
Question 27. Find the equation of the straight line passing through the point of intersection of the lines 5x – 6y -1 = 0 and perpendicular to the line 3x – 5y + 11 = 0.
Solution:

Let us considered M be the point of intersection of the given lines 5x – 6y – 1 = 0 and 3x + 2y + 5 = 0
On solving both the equations we get the point of intersection as M (-1, -1).
Now we find the slope of 3x – 5y + 11 = 0
5y = 3x + 11
y = 3x/5 + 11/5
On comparing y = mx + c, we get
m = 3/5
From the figure we can see that AP is perpendicular to line 3x – 5y + 11 = 0
So, the slope of AP = -5/3
Now the equation of AP is
y – y1 = m(x – x1)
y + 1 = -5/3(x + 1)
3y + 3 = -5x – 5
5x + 3y + 8 = 0
Hence, the equation of the line AP is 5x + 3y + 8 = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...