Class 11 RD Sharma Solutions – Chapter 23 The Straight Lines- Exercise 23.12 | Set 2
Last Updated :
18 Feb, 2022
Question 11. Find the equation of the right bisector of the line segment joining the points (a, b) and (a1, b1).
Solution:
Let us considered P(a, b) and Q(a1, b1) are the given points and O be the mid-point of line PQ.
So the coordinate O = ((a + a1)/, (b + b1)/2)
Slope of line PQ = 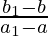
And the slope of right bisector of AB(m’) = 
The equation of required line is
y – y1 = m'(x – x1)
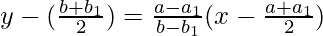
2x(a1 – a) + 2y(b1 – b) + a2 + b2 = a12 + b12
2x(a1 – a) + 2y(b1 – b) + (a2 + b2) – (a12 + b12) = 0
Hence, the equation of line is 2x(a1 – a) + 2y(b1 – b) + (a2 + b2) – (a12 + b12) = 0
Question 12. Find the image of the point (2, 1) with respect to the line mirror x + y – 5 = 0.
Solution:
Let us considered P(2, 1) be the image of Q(a, b) are the given points and O be the mid-point of line PQ.
So the coordinate O = ((2 + a)/2, (1 + b)/2)
And O point lie on the line x + y – 5 = 0
(2 + a)/2 + (1 + b)/2 – 5 = 0
a + b = 7 ………(1)
Here, x + y – 5 = 0 is perpendicular to PQ
So, (Slope of PQ) x (slope of AB) = -1
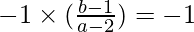
b – 1 = a – 2
b – a = -1 ………(2)
On solving eq(1) and (2), we get
a = 5 and b = 2
Hence, the image of (1, 2) in x + y – 5 = 0 is (4, 3)
Question 13. If the image of the point (2, 1) with respect to the line mirror be (5, 2), find the equation of the mirror.
Solution:
Let us considered A(5, 2) be image of B(2, -1) and O be the mid point of AB
So the coordinate O = (7/2, 3/2)
Let us considered PQ be the mirror and line AB perpendicular to PQ
So, (Slope of PQ) x (slope of AB) = -1
(2 – 1/5 – 2) x (slope of AB) = -1
(slope of AB) = -3
So the equation of the mirror is
y – 3/2 = -3(x – 7/2)
2y – 3 = -6x + 21
Hence, the equation of the mirror is 3x + y – 12 = 0
Question 14. Find the equation to the straight line parallel to 3x – 4y + 6 = 0 and passing through the middle point of the join points (2, 3) and (4, -1).
Solution:
It is given that A(2, 3) and B(4, -1) and O be the mid point of AB
So the coordinate O = (3, 1)
It is given that the equation to the straight line parallel to 3x – 4y + 6 = 0
So,
y = 3x/4 + 3/2
On comparing y = mx + c, we get
m = 3/4
Now put the value of m and (x1, y1) is eq(1), we get
The required equation of line is
y – y1 = m(x – x1)
y – 1 = 3/4(x – 3)
4y – 4 = 3x – 9
3x – 4y = 5
Hence, the equation of line is 3x – 4y = 5
Question 15. Prove that the lines 2x – 3y + 1 = 0, x + y = 3, 2x – 3y = 2 and x + y = 4 form a parallelogram.
Solution:
AS we know that in a parallelogram opposite sides are parallel and parallel sides have equal slope.
So, the slope of line 2x – 3y + 1 = 0
m1 = 2/3 …….(1)
The slope of line x + y = 3
m2 = -1 …….(2)
The slope of line 2x – 3y – 2 = 0
m3 = 2/3 …….(3)
The slope of line x + y = 4
m4 = -1 …….(4)
From (1), (2), (3) and (4), we get
We conclude that the opposite sides of ABCD have same slope
Hence, the given quadrilateral is parallelogram.
Question 16. Find the equation of a line drawn perpendicular to the line x/4 + y/6 = 1 through the point where it meets the y-axis.
Solution:
Let us considered the required equation of line is
y – y1 = m(x – x1) ……….(1)
The required line is perpendicular to the given line x/4 + y/6 = 1
When x = 0
y/6 = 1
y = 6
So, the point (x1, y1) is (0, 6)
It is given that the required equation of line is perpendicular to the line x/4 + y/6 = 1
So,
(slope of required line) x (slope of given line) = -1
m1 = -1/(-6/4) = 4/6 = 2/3
Now put the value of m’ and (x1, y1) is eq(1), we get
(y – 6) = 2/3(x – 0)
2x – 3y = -18
2x – 3y + 18 = 0
Hence, the equation of line is 2x – 3y + 18 = 0
Question 17. The perpendicular from the origin to the line y = mx + c meets it at the point (-1, 2). Find the values of m and c.
Solution:
Let us considered point O (0, 0) and P (-1, 2) and OP is perpendicular to the given line y = mx + c
So, (slope of OP) x (slope of line)=-1
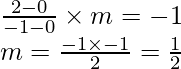
And point P lie on the line  so,
so,
2 = (1/2)(-1) + c
c = 2 + 1/2 = 5/2
Hence, the value of c = 5/2 and m = 1/2
Question 18. Find the equation of the right bisector of line segment joining the points (3, 4) and (-1, 2).
Solution:
Let us considered P(3, 4) and Q(-1, 2) are the given point and O be the mid point of AB
So, the coordinate O = (1, 3)
And the slope of line PQ is 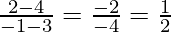
The right bisector of PQ is -2
The equation of the required line is
y – 3 = (-2)(x – 1)
y – 3 = -2x + 2
2x + y – 5 = 0
Hence, the required equation of line is 2x + y – 5 = 0
Question 19. The line through (h, 3) and (4, 1) intersects the line 7x – 9y – 19 = 0 at right angle. Find the value of h.
Solution:
Let us considered P (h, 3) and Q(4, 1) are the given points
Now the slope the line 7x – 9y – 19 = 0 is 7/9
It is given that line PQ is perpendicular to 7x – 9y – 19 = 0
so
7/9 x (1 – 3)/(4 – h) = -1
9h = 22
h = 22/9
Hence, the value of h is 22/9
Question 20. Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Solution:
Let us considered A(5, 2) be image of B(a, b) and O be the mid point of AB
So, the coordinate of O = ((3 + a)/2, (8 + b)/2)
O point lies on line x + 3y = 7
So, (3 + a)/2 + 3 x ((8 + b)/2) = 7
a + 13b + 13 = 0 ……(1)
It is given that line AB is perpendicular to mirror PQ
So, slope of AB x slope of PQ = -1
(b – 8/a – 3) x -1/3 = -1
3a – b – 1 = 0 ……(2)
On solving eq(1) and (2), we get
a = -1, b = -4
Hence, the image is (-1, -4)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...