Question 1. Find the equation of a line passing through the point (2, 3) and parallel to the line 3x – 4y + 5 = 0.
Solution:
Let us considered that the equation of line pass through point(2, 3) is
y – y1 = m(x – x1) ………(1)
It is given that the line is parallel to 3x – 4y + 5 = 0
So, the slope of 3x – 4y + 5 = 0
4y = 3x + 5
y = 3/4x + 5/4
On comparing y = mx + c, we get
m = 3/4
Now put the value of m and (x1,y1) is eq(1), we get
y – 3 = 3/4(x – 2)
4y – 12 = 3x – 6
3x – 4y = -12 + 6
3x – 4y = -6
Hence, the equation of line is 3x – 4y + 6 = 0
Question 2. Find the equation of the line passing through (3, 2) and perpendicular to the line x – 3y + 5 = 0.
Solution:
Let us considered that the equation of line pass through point(2, 3) is
y – y1 = m(x – x1) ………(1)
Here (x1, y1) is (3, 2) and m is slope of line and slope -1/m is taken as lines are perpendicular
It is given that the line is perpendicular to 3x – 4y + 5 = 0
3y = x + 5
y = x/3 + 5/3
On comparing y = mx + c, we get
m = 1/3
Now put the value of m and (x1,y1) is eq(1), we get
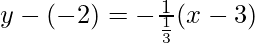
y + 2 = -3(x – 3) = -3x + 9
Hence, the equation of line is 3x + y = 7
Question 3. Find the equation of the perpendicular bisector of the line joining the points (1, 3) and (3, 1).
Solution:
Let us considered point A(1, 3) and B(3, 1)
As we know that any line that is perpendicular bisector which means line is perpendicular
to the given line and one end point is the mid-point of that line.
So, the line AB has the mid-point
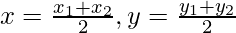
(x1,y1) = 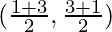 = (2, 2)
= (2, 2)
Also slope of the line AB is
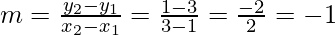
Now we find the equation of perpendicular bisector:
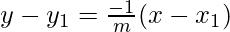
y – 2 = 1(x – 2)
y – 2 = x – 2
y = x
Question 4. Find the equation of the altitudes of ∆ABC whose vertices are A(1, 4), B(-3, 2), and C(-5, -3).
Solution:
Given that ABC is a triangle whose vertices are A(1, 4), B(-3, 2), and C(-5, -3)
Find: the equation of the altitudes of ∆ABC
So, let the perpendiculars of the triangle on the side AB, BC and AC are be CF, AD and FB

The slope of the side AB = 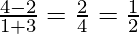
Slope of CF =  = -2
= -2
So, the equation of side CF is
y – y1 = m(x – x1)
y + 3 = -2(x + 5)
y + 3 = -2x – 10
y = -2x – 13
The slope of the side BC = 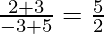
And the slope of AD = 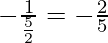
So, the equation of side AD is
y – y1 = m(x – x1)
y – 4 = 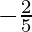 (x – 1)
(x – 1)
5y – 20 = -2x + 2
5y = -2x – 22
The slope of the side AC = 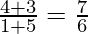
And the slope of EB = 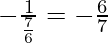
So, the equation of side FB is
y – y1 = m(x – x1)
y – 2 = -6/7(x + 3)
7y – 14 = -6x – 18
7y = -6x – 4
Hence, the equations of the altitudes of ∆ABC are
AD = 2x + 5y + 22 = 0
CF = 2x + y + 13 = 0
FB = 6x + 7y + 4 = 0
Question 5. Find the equation of a line which is perpendicular to the line √3x – y + 5 = 0 and which cuts off an intercept of 4 units with the negative direction of y-axis.
Solution:
Let us considered the required equation of line is
y – y1 = m'(x – x1) ……….(1)
So, point (x1, y1) = (0, -4)
It is given that the line is perpendicular to line 3x – y + 5 = 0
So, the slope of 3x – y + 5 = 0
y = 3x + 5
On comparing y = mx + c, we get
m = √3
As we know that the line is perpendicular to the line 3x – y + 5 = 0
So, the slope is m’ = -1/m = -1/√3
Now put the value of m’ and (x1, y1) is eq(1), we get
y – (-4) = -1/√3(x – 0)
y + 4 = -x/√3
x + √3y + 4√3 = 0
Question 6. If the image of the point (2, 1) with respect to a line mirror is (5, 2) find the equation of the mirror.
Solution:
Let us considered the image of point Q(2, 1) is R(5, 2) and O is the mid point of line QR
So, the coordinate of O is ((2 + 5)/2, (1 + 2)/2) = (7/2, 3/2)
Now let us considered AB be the mirror and line QR is perpendicular to AB
So, m1 x m2 = -1
Here, m1 is the slope of AB and m2 is the slope of CD
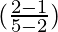 x m2 = -1
x m2 = -1
1/3 x m2 = -1
m2 = -3
So the slope of CD is -3
Now we find the equation of CD
y – y1 = m(x – x1)
y -(3/2) = (-3)(x – 7/2)
(2y -3)/2 = -3x +21/2
2y – 3 = -6x + 21
6x + 2y = 24
3x + y = 12
Hence, the equation of the mirror is 3x + y – 12 =0
Question 7. Find the equation of the straight line through the point (α, β) and perpendicular to the line lx + my + n = 0.
Solution:
Let us considered the required equation of line is
y – y1 = m'(x – x1) ……….(1)
So, point (x1, y1) = (α, β)
It is given that the line is perpendicular to the line lx + my + n = 0
So, the slope of line lx + my + n = 0 is
y = -lx/m – n/m
On comparing y = mx + c, we get
m = -l/m
As we know that the line is perpendicular to the line lx + my + n = 0
So, the slope is m’ = -1/m = m/l
Now put the value of m’ and (x1, y1) is eq(1), we get
y – β = m/l(x – α)
ly + mx = ma + lβ
m(x – a) = l(y – β)
Hence, the equation of the straight line is m(x – a) = l(y – β)
Question 8. Find the equation of the straight line perpendicular to 2x – 3y = 5 and cutting off an intercept 1 on the positive direction of the x-axis.
Solution:
Let us considered the required equation of line is
y – y1 = m'(x – x1) ……….(1)
So, point (x1, y1) = (1, 0)
It is given that the line is perpendicular to the line 2x – 3y = 5
So, the slope of line 2x – 3y = 5 is
y = -2x/3 + 5/3
On comparing y = mx + c, we get
m = -2/3
As we know that the line is perpendicular to the line lx + my + n = 0
So, the slope is m’ = -1/m = 3/2
Now put the value of m’ and (x1, y1) is eq(1), we get
y – y1 = m(x – x1)
y – 0 = 2/3(x – 1)
y = -3/2(x – 1)
2y = -3x + 3
Hence, the equation of the required line is 3x + 2y – 3 = 0
Question 9. Find the equation of the straight line perpendicular to 5x – 2y = 8 and which passes through the mid-point of the segment joining (2, 3) and (4, 5).
Solution:
Let us considered point A(2, 3) and (4, 5) and O be the mid point of AB
so the coordinates of O = ((2 + 4)/2, (3 + 5)/ 2) = (3, 4)
Let us considered the required equation of line is
y – y1 = m'(x – x1) ……….(1)
Here (x1,y1) is (3, 4)
It is given that the line is perpendicular to the line 5x – 2y = 8
So, the slope of line 5x – 2y = 8 is
y = 5x/2 – 4
On comparing y = mx + c, we get
m = 5/2
As we know that the line is perpendicular to the line 5x – 2y = 8
So, the slope is m’ = -1/m = -2/5
Putting m and (x1,y1) in (1), we get
y – 4 = (-2/5)(x – 3)
5y + 2x = 26
2x + 5y – 26 = 0
Hence, the equation of the required line is 2x + 5y – 26 = 0
Question 10. Find the equation of the straight line which has y-intercept equal to 4/3 and is perpendicular to 3x – 4y + 11 = 0.
Solution:
Let us considered the required equation of line is
y – y1 = m'(x – x1) ……….(1)
Here (x1, y1) is (0, 4/3)
It is given that the line is perpendicular to the line 3x – 4y + 11 = 0.
So, the slope of line 3x – 4y + 11 = 0 is
y = 3x/4 – 11/4
On comparing y = mx + c, we get
m = 3/4
As we know that the line is perpendicular to the line 3x – 4y + 11 = 0.
So, the slope is m’ = -1/m = -4/3
Putting m and (x1, y1) in (1), we get
y – 4/3 = (-4/3)(x – 0)
4x + 3y – 4 = 0
Hence, the equation of the required line is 4x + 3y – 4 = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...