Class 11 RD Sharma Solutions – Chapter 23 The Straight Lines- Exercise 23.10 | Set 2

Question 11. Find the orthocenter of the triangle the equations of whose sides are x + y = 1, 2x + 3y = 6, and 4x – y + 4 = 0.

Solution:

Let us considered ABC is a triangle, in which A, B, and C are the vertices of the triangle

So according to the question the equations of the sides of the triangle are:

AB = x + y = 1  …..(1)

BC = 2x + 3y = 6  …..(2)

AC = 4x – y + 4   …..(3)

On solving eq (1) and (2), we get point B(-3, 4)

On solving eq (1) and (3), we get point A(-3/5, 8/5)

Now the altitude from A to BC is

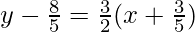
10y – 16 = 151x + 9

15x – 10y + 25 = 0

3x – 2y + 5 = 0   …..(4)

Similarly, the altitude form B to AC  given by

y – 4 = -1/4(x + 3)

4y – 16 = -x -3

4y – 16 = -x – 3

x + 4 – 13 = 0    …..(5)

On solving eq(4) and (5) we get 

orthocenter of the triangle i.e., O(3/7, 22/7) 

Question 12. The sides AB, BC, and CA of a triangle ABC are 5x – 3y + 2 = 0, x – 3y – 2 = 0, and x + y – 6 = 0 respectively. Find the equation of the altitude through the vertex A.

Solution:

According to the question

ABC is a triangle in which the equations of the sides are:

AB = 5x – 3y + 2 = 0

BC = x – 3y – 2 = 0

CA =  x + y – 6 = 0

On solving the above equations of AB, BC and CA we get

the coordinates of the vertices of the triangle ABC

B = (-1, -1)

A = (2, 4)

C = (5, 1)

Now the slope of BC = 1/3 then slope of AE = -3

Slope of AC = -1 then the slope of BD = 1

Slope of AB = 5/3 then the slope of CF = -3/5

Let us assume AD, BE, CF are altitudes of ∆ABC

So, the equation are

BD = y + 1 = 1(x + 1) ⇒ x – y = 0

AE = y – 4 = -3(x – 2) ⇒ 3x + y = 10

CF = y – 1 = 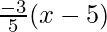⇒ 3x + 5y = 20

Hence, the equation of the altitude through the vertex A is 3x + y = 10

Question 13. Find the coordinates of the orthocenter of the triangle whose vertices are (-1, 3), (2, -1), and (0, 0).

Solution:

Let us considered ABC is a triangle whose vertices are A(-1, 3), B(2, -1), and D(0, 0).

Here, AD ⊥ BC, CF ⊥ AB, and BE ⊥ AC

Let us assume O be the orthocenter of triangle 

So, O(h, k)

Now, AO⊥BC

(slope of AO) * (slope of BC) = -1  

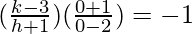
k – 3 = 2(h + 1)

k – 2h = 5  …..(1)

And BO ⊥ AC

(slope of BO) * (slope of AC) = -1

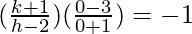
3(k + 1) = h – 2

3k – h = -5    …..(2)

Now from eq(1) and (2), we get the orthocenter O of triangle is (-4,-3)

Question 14. Find the coordinates of the incentre and centroid of the triangle whose sides have the equations 3x – 4y = 0, 12y + 5x = 0 and y – 15 = 0.

Solution:

Let us considered ABC be the triangle whose sides BC, CA, and AB have the equations 

BC = y – 15 = 0

AC = 3x – 4y = 0

AB = 5x + 12y = 0  

On solving the above equations we get

A(0, 0), B(-36, 15), C(20, 15) 

Now the centroid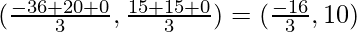

For incentre, we have

a = BC =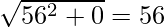 

b = CA =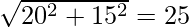 

c = AB =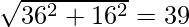 

Now the coordinates of incentre are

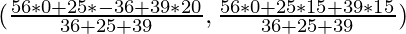
= (-1, 8)

Question 15. Prove that the lines√3x + y = 0, √3y + x = 0, √3x + y = 1 and √3y + x = 1 form a rhombus.

Solution:

Let us considered ABCD be a quadrilateral with sides AB, BC, CD, BA as 

√3x + y = 0, √3y + x = 0, √3x + y = 1 and √3y + x = 1

So, the slope of AB = -√3   …..(1)

The slope of BC = -1/√3     …..(2)

The slope of CD = -√3        …..(3)

The slope of DA = -1/√3     …..(4)

From eq (1), (2), (3) and (4) we conclude that the slope opposite sides of quadrilateral are equal.

So, the opposite sides are parallel.

Hence, ABCD is a parallelogram.

We also conclude that the distance between (AD and BC) and (DC and AB) is equal =1 unit

So, sides AD = AB = DC

Hence, the ABCD is a rhombus

Hence, proved 

Question 16. Find the equation of line passing through the intersection of the lines 3x + y = 5 and x + 3y + 8 = 0 and parallel to the line 3x + 4y = 7.

Solution:

Given that the equations of lines are:

2x + y = 5  

x + 3y + 8 = 0

On solve the above equations we get the

intersection point(23/5, -12/5)

It is given that the line is parallel to 3x + 4y = 7 and passing through above point(23/5, -12/5)

So the equation of line is 

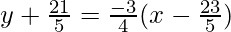
20y + 84 = -15x + 69

15x + 20y + 15 = 0

3x + 4y + 3 = 0

Question 17. Find the equation of the line passing through the point of intersection of the lines 5x – 6y – 1 = 0 and perpendicular to the line 3x – 5y + 11 = 0.

Solution:

Given that the equations of lines are:

5x – 6y – 1 = 0  

2y + 5 = 0

On solve the above equations we get the

intersection point(-1, 1)

It is given that the line is perpendicular to 3x – 5y + 11 = 0 and passing through above point(-1, 1)

So, the equation of line is 

(y + 1) = -5/3(x + 1)

3y + 5x + 8 = 0