Question 1. Find the locus of a point equidistant from the point (2, 4) and the y-axis.
Solution:
Let C (a, b) be any point on the locus and let A (2, 4) and B (0, b). We are given,
=> CA = CB
=> CA2 = CB2
Using distance formula, we get,
=> (a − 2)2 + (b − 4)2 = (a − 0)2 + (b − b)2
=> a2 + 4 − 4a + b2 + 16 − 8b = a2
=> b2 − 4a − 8b + 20 = 0
Replacing (a, b) with (x, y), we get the locus of our point,
=> y2 − 4x − 8y + 20 = 0
Therefore, locus of the point is y2 − 4x − 8y + 20 = 0.
Question 2. Find the equation of the locus of a point that moves such that the ratio of its distance from (2, 0) and (1, 3) is 5:4.
Solution:
Let C (a, b) be any point on the locus and let A (2, 0) and B (1, 3). We are given,
=> CA/CB = 5/4
=> CA2/CB2 = 25/16
Using distance formula, we get,
=> 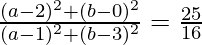
=> 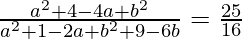
=> 16 (a2 + 4 − 4a + b2) = 25 (a2 + 1 − 2a + b2 + 9 − 6b)
=> 9a2 + 9b2 + 14a − 150b + 186 = 0
Replacing (a, b) with (x, y), we get the equation of the locus of our point,
=> 9x2 + 9y2 + 14x − 150y + 186 = 0
Therefore the locus of the point is 9x2 + 9y2 + 14x − 150y + 186 = 0.
Question 3. A point moves as so that the difference of its distances from (ae, 0) and (−ae, 0) is 2a, prove that the equation to its locus is x2/a2 − y2/b2 = 1, where b2 = a2 (e2 − 1).
Solution:
Let C (h, k) be any point on the locus and let A (ae, 0) and B (−ae, 0). We are given,
=> CA − CB = 2a
Using distance formula, we get,
=> 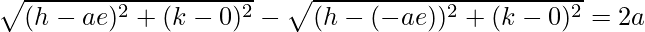
=> 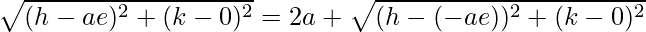
Squaring both sides, we get,
=> 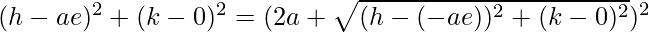
=> h2 + a2e2 − 2aeh + k2 = 4a2 + (h + ae)2 + k2 + 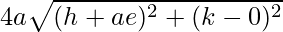
=> h2 + a2e2 − 2aeh + k2 = 4a2 + h2 + a2e2 + 2aeh + k2 + 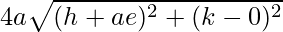
=> −4aeh − 4a2 = 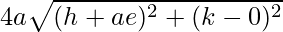
Squaring both sides again, we get,
=> −(eh + a) = (h + ae)2 + k2
=> e2h2 + a2 + 2aeh = h2 + a2e2 + 2aeh + k2
=> h2 (e2 – 1) – k2 = a2 (e2 – 1)
=> 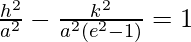
As we are given, b2 = a2 (e2 − 1), we get,
=> h2/a2 − k2/b2 = 1
Replacing (h, k) with (x, y), we get the equation of the locus of our point,
=> x2/a2 − y2/b2 = 1
Hence proved.
Question 4. Find the locus of a point such that the sum of its distances from (0, 2) and (0, −2) is 6.
Solution:
Let C (a, b) be any point on the locus and let A (0, 2) and B (0, −2). We are given,
=> CA + CB = 6
Using distance formula, we get,
=> 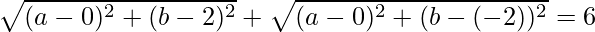
=> 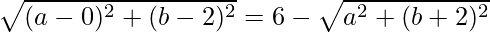
Squaring both sides, we get,
=> a2 + b2 + 4 − 4b= 36 + a2 + b2 + 4 + 4b − 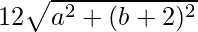
=> −8b − 36 = 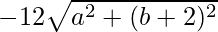
=> −4 (2b + 9) = 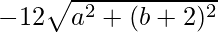
Squaring both sides again, we get,
=> (2b + 9)2 = 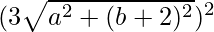
=> 4b2 + 81 + 36b = 9a2 + 9b2 + 36b + 36
=> 9a2 + 5b2 = 45
Replacing (a, b) with (x, y), we get the locus of our point,
=> 9x2 + 5y2 = 45
Therefore the locus of the point is 9x2 + 5y2 = 45.
Question 5. Find the locus of a point which is equidistant from (1, 3) and x-axis.
Solution:
Let C (a, b) be any point on the locus and let A (1, 3) and B (a, 0). We are given,
=> CA = CB
=> CA2 = CB2
Using distance formula, we get,
=> (a − 1)2 + (b − 3)2 = (a − a)2 + (b − 0)2
=> a2 + 1 − 2a + b2 + 9 − 6b = b2
=> a2 − 2a − 6b + 10 = 0
Replacing (a, b) with (x, y), we get the locus of our point,
=> x2 − 2x − 6y + 10 = 0
Therefore the locus of the point is x2 − 2x − 6y + 10 = 0.
Question 6. Find the locus of a point that moves such that its distance from the origin is three times is distance from x-axis.
Solution:
Let C (a, b) be any point on the locus and let A (0, 0) and B (a, 0). We are given,
=> CA = 3 CB
=> CA2 = 9 CB2
Using distance formula, we get,
=> (a − 0)2 + (b − 0)2 = 9 [(a − a)2 + (b − 0)2]
=> a2 + b2 = 9b2
=> a2 = 8b2
Replacing (a, b) with (x, y), we get the locus of our point,
=> x2 = 8y2
Therefore the locus of the point is x2 = 8y2.
Question 7. A (5, 3), B (3, −2) are two fixed points, find the equation to the locus of a point P which moves so that the area of the triangle PAB is 9 sq. units.
Solution:
Let P (a, b) be any point on the locus and we have A (5, 3) and B (3, −2). We are given,
=> Area of the triangle PAB = 9
=> 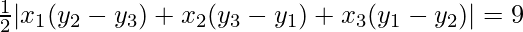
=> |5(−2−b) + 3(b−3) + h(3+2)| = 18
=> |5a − 2b − 19| = 18
=> 5a − 2b − 19 = ±18
=> 5a − 2b − 37 = 0 or 5a − 2b − 1 = 0
Replacing (a, b) with (x, y), we get the locus of our point,
=> 5x − 2y − 37 = 0 or 5x − 2y − 1 = 0
Therefore the equation to the locus of the point is 5x − 2y − 37 = 0 or 5x − 2y − 1 = 0.
Question 8. Find the locus of a point such that the line segment having endpoints (2, 0) and (−2, 0) subtend a right angle at that point.
Solution:
Let C (a, b) be any point on the locus and let A (2, 0) and B (−2, 0).
We are given ∠ ACB = 90o
=> AB2 = CA2 + CB2
Using distance formula, we get,
=> (2+2)2 + (0−0)2 = (a−2)2 + (b−0)2 + (a+2)2 + (b−0)2
=> 16 = a2 + 4 − 4a + b2 + a2 + 4 + 4a + b2
=> 2a2 + 2b2 + 8 = 16
=> a2 + b2 = 4
Replacing (a, b) with (x, y), we get the locus of our point,
=> x2 + y2 = 4
Therefore the locus of the point is x2 + y2 = 4.
Question 9. A (−1, 1), B (2, 3) are two fixed points, find the locus of a point P which moves so that the area of the triangle PAB is 8 sq. units.
Solution:
Let P (a, b) be any point on the locus and we have A (−1, 1) and B (2, 3). We are given,
=> Area of the triangle PAB = 8
=> 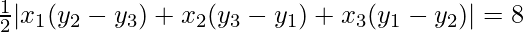
=> |−1(3−b) + 2(b−1) + a(1−3)| = 16
=> |−2a + 3b − 5| = 16
=> −2a + 3b − 5 = ±16
=> 2a − 3b + 21 = 0 or 2a − 3b − 11 = 0
Replacing (a, b) with (x, y), we get the locus of our point,
=> 2x − 3y + 21 = 0 or 2x − 3y − 11 = 0
Therefore the locus of the point is 2x − 3y + 21 = 0 or 2x − 3y − 11 = 0.
Question 10. A rod of length l slides between two perpendicular lines. Find the locus of the point on the rod which divides it in the ratio 1:2.
Solution:
Let C (h, k) be any point on the locus and let AB = l (given) be the length of the rod. Suppose, coordinates of A and B are (a, 0) and (0, b) respectively.
According to the question,
=> h = 2a/3
=> a = 3h/2 . . . . (1)
And k = b/3
=> b = 3k . . . . (2)
Let the origin be O (0, 0). Now we know △ AOB is right-angled.
=> AB2 = OA2 + OB2
=> l2 = [(a−0)2 + (0−0)2] + [(0−0)2 + (b−0)2]
=> a2 + b2 = l2
Using (1) and (2), we get,
=> (3h/2)2 + (3k)2 = l2
=> 9h2/4 + 9k2 = l2
=> 9h2 + 36k2 = 4l2
Replacing (h, k) with (x, y), we get the locus of our point,
=> 9x2 + 36y2 = 4l2
Therefore the locus of the point is 9x2 + 36y2 = 4l2.
Question 11. Find the locus of the mid-point of the portion of the line x cos α + y sin α = p which is intercepted between the axes.
Solution:
We are given,
=> x cos α + y sin α = p
=> 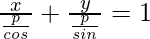
Intercepts on x-axis and y -axis are p/cos α and p/sin α respectively.
Suppose (x, y) is the mid-point of the portion of the given line which is intercepted between the axes.
=> (x, y) = 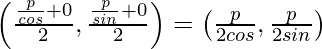
=> x = p/2 cos α and y = p/2 sin α
=> 2 cos α = p/x and 2 sin α = p/y
Squaring both sides of these, we get,
=> 4 cos2 α = p2/x2 . . . . (1)
=> 4 sin2 α = p2/y2 . . . . (2)
Adding (1) and (2), we get,
=> 4 cos2 α + 4 sin2 α = p2/x2 + p2/y2
=> p2/x2 + p2/y2 = 4
=> p2 (x2 + y2) = 4x2y2
Therefore the locus of the mid-point is p2 (x2 + y2) = 4x2y2.
Question 12. If O is the origin and Q is the variable point on y2 = x. Find the locus of the mid-point of OQ.
Solution:
Let P (h, k) be the point on the locus and let Q (a, b).
According to the question,
=> h = (a+0)/2 and k = (b+0)/2
=> h = a/2 and k = b/2
=> a = 2h and b = 2k
As point Q lies on y2 = x, we get,
=> (2k)2 = 2h
=> 4k2 = 2h
=> 2k2 = h
Replacing (h, k) with (x, y), we get the locus of our point,
=> 2y2 = x
Therefore the locus of the mid-point is 2y2 = x.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...