Sum the following series to n terms:
Question 1. 3 + 5 + 9 + 15 + 23 + . . . . n terms
Solution:
We are given the series: 3 + 5 + 9 + 15 + 23 + . . . . n terms.
Let’s take S as the sum of this series. Therefore,
S = 3 + 5 + 9 + 15 + 23 + . . . . + an–1 + an . . . .(1)
S = 3 + 5 + 9 + 15 + 23 + . . . . + an–2 + an–1 + an . . . .(2)
On subtracting (2) from (1), we get
=> S – S = [3 + (5 + 9 + 15 + 23 + . . . . + an–1 + an)] – [(3 + 5 + 9 + 15 + 23 + . . . . + an–2 + an–1) +an]
=> 0 = 3 + [(5 – 3) + (9 – 5) + (15 – 9) + . . . . + (an – an–1)] – an
=> an = 3 + [2 + 4 + 6 + . . . . (n–1) terms]
As the series 2+ 4 + 6 + . . . . (n–1) terms is an A.P., with first term(a) = 2 and common difference(d) = 4–2 = 2. So, we get,
=> an = 3 + (n–1) [2(2)+(n–2)2]/2
= 3+ (n–1) [4+2n–4]/2
= 3 + n(n–1)
= n2 – n+3
Now we have to summate our nth term to find the sum(Sn) of this series.
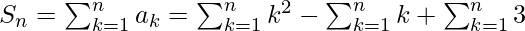
= 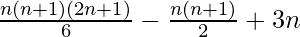
= ![Rendered by QuickLaTeX.com n\left[\frac{(n+1)(2n+1)-3(n+1)+18}{6}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-82f5aa434d1832757e86433fa13e9416_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n}{6}\left[2n^2+n+2n+1-3n-3+18\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7797f6d083a7668868ec2cb3788bc805_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n}{6}\left[2n^2+16\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eeeaa5138c87ad3c3eea78fea0a47627_l3.png)
= 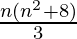
Therefore, sum of the given series up to n terms is 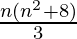 .
.
Question 2. 2 + 5 + 10 + 17 + 26 + . . . . n terms
Solution:
We are given the series: 2 + 5 + 10 + 17 + 26 + . . . . n terms.
Let’s take S as the sum of this series. Therefore,
S = 2 + 5 + 10 + 17 + 26 + . . . . + an–1 + an . . . .(1)
S = 2 + 5 + 10 + 17 + 26 + . . . . + an–2 + an–1 + an . . . .(2)
On subtracting (2) from (1), we get
=> S – S = [2 + (5 + 10 + 17 + 26 + . . . . + an–1 + an)] – [(2 + 5 + 10 + 17 + 26 + . . . . + an–2 + an–1) +an]
=> 0 = 2 + [(5 – 2) + (10 – 5) + (17 – 10) + . . . . + (an – an–1)] – an
=> an = 2 + [3 + 5 + 7 + . . . . (n–1) terms]
As the series 3 + 5 + 7 + . . . . (n–1) terms is an A.P., with first term(a) = 3 and common difference(d) = 5–3 = 2. So, we get,
=> an = 2 + (n–1) [2(3)+(n–2)2]/2
= 2+ (n–1) [6+2n–4]/2
= 2 + (n–1)(n+1)
= n2 – 1 + 2
= n2 + 1
Now we have to summate our nth term to find the sum(Sn) of this series.
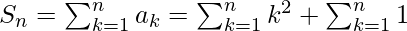
= 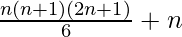
= 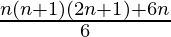
= 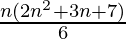
Therefore, sum of the given series up to n terms is 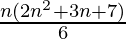 .
.
Question 3. 1 + 3 + 7 + 13 + 21 + 31 + . . . . n terms
Solution:
We are given the series: 1 + 3 + 7 + 13 + 21 + 31 + . . . . n terms.
Let’s take S as the sum of this series. Therefore,
S = 1 + 3 + 7 + 13 + 21 + 31 + . . . . + an–1 + an . . . .(1)
S = 1 + 3 + 7 + 13 + 21 + 31 + . . . . + an–2 + an–1 + an . . . .(2)
On subtracting (2) from (1), we get
=> S – S = [1 + (3 + 7 + 13 + 21 + 31 + . . . . + an–1 + an)] – [(1 + 3 + 7 + 13 + 21 + 31 + . . . . + an–2 + an–1) + an]
=> 0 = 1 + [(3 – 1) + (7 – 3) + (13 – 7) + . . . . + (an – an–1)] – an
=> an = 1 + [2 + 4 + 6 + . . . . (n–1) terms]
As the series 2 + 4 + 6 + . . . . (n–1) terms is an A.P., with first term(a) = 2 and common difference(d) = 4–2 = 2. So, we get,
=> an = 1 + (n–1) [2(2)+(n–2)2]/2
= 1+ (n–1) [4+2n–4]/2
= 1 + n(n–1)
= n2 – n+1
Now we have to summate our nth term to find the sum(Sn) of this series.
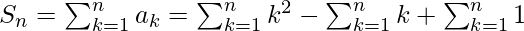
= 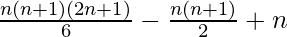
= 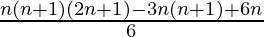
= 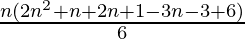
= 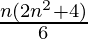
= 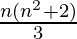
Therefore, sum of the given series up to n terms is 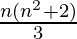 .
.
Question 4. 3 + 7 + 14 + 24 + 37 + . . . . n terms
Solution:
We are given the series: 3 + 7 + 14 + 24 + 37 + . . . . n terms.
Let’s take S as the sum of this series. Therefore,
S = 3 + 7 + 14 + 24 + 37 + . . . . + an–1 + an . . . .(1)
S = 3 + 7 + 14 + 24 + 37 + . . . . + an–2 + an–1 + an . . . .(2)
On subtracting (2) from (1), we get
=> S – S = [3 + (7 + 14 + 24 + 37 + . . . . + an–1 + an)] – [(3 + 7 + 14 + 24 + 37 + . . . . + an–2 + an–1) + an]
=> 0 = 3 + [(7 – 3) + (14 – 7) + (24 – 14) + . . . . + (an – an–1)] – an
=> an = 3 + [4 + 7 + 10 + . . . . (n–1) terms]
As the series 4 + 7 + 10 + . . . . (n–1) terms is an A.P., with first term(a) = 4 and common difference(d) = 7–4 = 3. So, we get,
=> an = 3 + (n–1) [2(4)+(n–2)3]/2
= 3+ (n–1) [8+3n–6]/2
= 3 + (n–1)(3n+2)/2
= 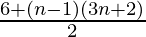
= 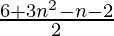
= 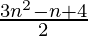
Now we have to summate our nth term to find the sum(Sn) of this series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n} a_k = \frac{1}{2}\left[\sum_{k=1}^{n} 3k^2 - \sum_{k=1}^{n} k + \sum_{k=1}^{n} 4\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-99402a0755158180d2fe9611619891cd_l3.png)
= 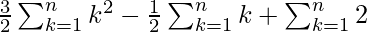
= ![Rendered by QuickLaTeX.com \frac{3}{2}[\frac{n(n+1)(2n+1)}{6}]-\frac{1}{2}[\frac{n(n+1)}{2}]+2n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-75b8753963844418cefdbad375622fae_l3.png)
= 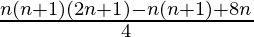
= 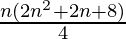
= 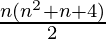
Therefore, sum of the given series up to n terms is 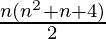 .
.
Question 5. 1 + 3 + 6 + 10 + 15 + . . . . n terms
Solution:
We are given the series: 1 + 3 + 6 + 10 + 15 + . . . . n terms.
Let’s take S as the sum of this series. Therefore,
S = 1 + 3 + 6 + 10 + 15 + . . . . + an–1 + an . . . .(1)
S = 1 + 3 + 6 + 10 + 15 + . . . . + an–2 + an–1 + an . . . .(2)
On subtracting (2) from (1), we get
=> S – S = [1 + (3 + 6 + 10 + 15 + . . . . + an–1 + an)] – [(1 + 3 + 6 + 10 + 15 + . . . . + an–2 + an–1) + an]
=> 0 = 1 + [(3 – 1) + (6 – 3) + (10 – 6) + . . . . + (an – an–1)] – an
=> an = 1 + [2 + 3 + 4 + . . . . (n–1) terms]
As the series 2 + 3 + 4 + . . . . (n–1) terms is an A.P., with first term(a) = 2 and common difference(d) = 3–2 = 1. So, we get,
=> an = 1 + (n–1) [2(2)+(n–2)1]/2
= 1+ (n–1) [4+n–2]/2
= 1 + (n–1)(n+2)/2
= 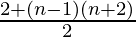
= 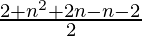
= 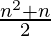
Now we have to summate our nth term to find the sum(Sn) of this series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n} a_k = \frac{1}{2}\left[\sum_{k=1}^{n} k^2 + \sum_{k=1}^{n} k\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b2af88c121bf0bef7cce48a453309a9e_l3.png)
= 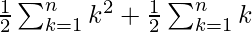
= ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{n(n+1)(2n+1)}{6}\right] + \frac{1}{2}\left[\frac{n(n+1)}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3372b75b93a6b2d3f12f0827d7f4091_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n(n+1)}{2}\left[\frac{2n+1}{6}+\frac{1}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c55e5d6c454c1c793902ff4aa4fcdadc_l3.png)
= 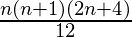
= 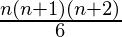
Therefore, sum of the given series up to n terms is 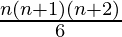 .
.
Question 6. 1 + 4 + 13 + 40 + 121 + . . . . n terms
Solution:
We are given the series: 1 + 4 + 13 + 40 + 121 + . . . . n terms.
Let’s take S as the sum of this series. Therefore,
S = 1 + 4 + 13 + 40 + 121 + . . . . + an–1 + an . . . .(1)
S = 1 + 4 + 13 + 40 + 121 + . . . . + an–2 + an–1 + an . . . .(2)
On subtracting (2) from (1), we get
=> S – S = [1 + (4 + 13 + 40 + 121 + . . . . + an–1 + an)] – [(1 + 4 + 13 + 40 + 121 + . . . . + an–2 + an–1) + an]
=> 0 = 1 + [(4 – 1) + (13 – 4) + (40 – 13) + . . . . + (an – an–1)] – an
=> an = 1 + [3 + 9 + 27 + . . . . (n–1) terms]
As the series 3 + 9 + 27 + . . . . (n–1) terms is a G.P., with first term(a) = 3 and common ratio(r) = 9/3 = 3. So, we get,
=> an = 1 + 3(3n-1–1)/(3–1)
= 1+ 3(3n-1–1)/2
= 1 + 3n/2 – 3/2
= 3n/2 – 1/2
Now we have to summate our nth term to find the sum(Sn) of this series.
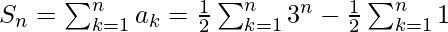
= 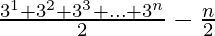
= 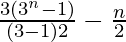
= 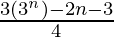
= 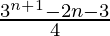
Therefore, sum of the given series up to n terms is 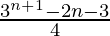 .
.
Question 7. 4 + 6 + 9 + 13 + 18 + . . . . n terms
Solution:
We are given the series: 4 + 6 + 9 + 13 + 18 + . . . . n terms.
Let’s take S as the sum of this series. Therefore,
S = 4 + 6 + 9 + 13 + 18 + . . . . + an–1 + an . . . .(1)
S = 4 + 6 + 9 + 13 + 18 + . . . . + an–2 + an–1 + an . . . .(2)
On subtracting (2) from (1), we get
=> S – S = [4 + (6 + 9 + 13 + 18 + . . . . + an–1 + an)] – [(4 + 6 + 9 + 13 + 18 + . . . . + an–2 + an–1) + an]
=> 0 = 4 + [(6 – 4) + (9 – 6) + (13 – 9) + . . . . + (an – an–1)] – an
=> an = 4 + [2 + 3 + 4 + . . . . (n–1) terms]
As the series 2 + 3 + 4 + . . . . (n–1) terms is an A.P., with first term(a) = 2 and common difference(d) = 3–2 = 1. So, we get,
=> an = 4 + (n–1) [2(2)+(n–2)1]/2
= 4 + (n–1)(n+2)/2
= 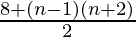
= 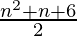
Now we have to summate our nth term to find the sum(Sn) of this series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n} a_k = \frac{1}{2}\left[\sum_{k=1}^{n} n^2 + \sum_{k=1}^{n} n + \sum_{k=1}^{n} 6\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-551c804fe5cb1a1a47479074e085b200_l3.png)
= 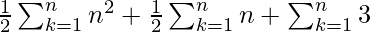
= ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{n(n+1)(2n+1)}{6}] + \frac{1}{2}[\frac{n(n+1)}{2}] + 3n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b3090413826e613f139b2b1d8e2b602_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n[(n+1)(2n+1)+3(n+1)+36]}{12}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-02fec34e7b8da85beb05b7cfab65075d_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n[2n^2+6n+40]}{12}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-42c60dafbdf1d25ceaa09f528ed6b476_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n[n^2+3n+20]}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4cf717426fe200a087c762e57d395ca4_l3.png)
Therefore, sum of the given series up to n terms is ![Rendered by QuickLaTeX.com \frac{n[n^2+3n+20]}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5d7b281b52a43b0d63cf1fc1ce1e0b06_l3.png) .
.
Question 8. 2 + 4 + 7 + 11 + 16 + . . . . n terms
Solution:
We are given the series: 2 + 4 + 7 + 11 + 16 + . . . . n terms.
Let’s take S as the sum of this series. Therefore,
S = 2 + 4 + 7 + 11 + 16 + . . . . + an–1 + an . . . .(1)
S = 2 + 4 + 7 + 11 + 16 + . . . . + an–2 + an–1 + an . . . .(2)
On subtracting (2) from (1), we get
=> S – S = [2 + (4 + 7 + 11 + 16 + . . . . + an–1 + an)] – [(2 + 4 + 7 + 11 + 16 + . . . . + an–2 + an–1) + an]
=> 0 = 2 + [(4 – 2) + (7 – 4) + (11 – 7) + . . . . + (an – an–1)] – an
=> an = 2 + [2 + 3 + 4 + . . . . (n–1) terms]
As the series 2 + 3 + 4 + . . . . (n–1) terms is an A.P., with first term(a) = 2 and common difference(d) = 3–2 = 1. So, we get,
=> an = 2 + (n–1) [2(2)+(n–2)1]/2
= 2 + (n–1)(n+2)/2
= 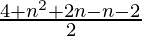
= 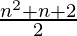
Now we have to summate our nth term to find the sum(Sn) of this series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n} a_k = \frac{1}{2}\left[\sum_{k=1}^{n} n^2 + \sum_{k=1}^{n} n + \sum_{k=1}^{n} 2\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-670b8588f7256324e9679701dc94183b_l3.png)
= 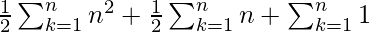
= ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{n(n+1)(2n+1)}{6}]+\frac{1}{2}[\frac{n(n+1)}{2}]+n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-64a47d8fc96e5eab7fdb2c45386e90a3_l3.png)
= ![Rendered by QuickLaTeX.com \frac{n[(n+1)(2n+1)+3(n+1)+12n]}{12}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e5c0974f424d8538e80902840cc83691_l3.png)
= 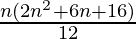
= 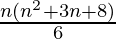
Therefore, sum of the given series up to n terms is 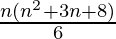 .
.
Question 9. 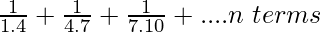
Solution:
The nth term of the given series would be,
an = 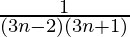
= ![Rendered by QuickLaTeX.com \frac{1}{3}\left[\frac{1}{3n-2}-\frac{1}{3n+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f1e6fc59fd5cc735284cb5e21c7d83e7_l3.png)
Now we have to summate our nth term to find the sum(Sn) of this series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n} a_k = \frac{1}{3}\sum_{k=1}^{n} \left[\frac{1}{3n-2}-\frac{1}{3n+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d4341991c3da845541d0027baaac7adb_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{3}\left[(1-\frac{1}{4})+(\frac{1}{4}-\frac{1}{7})+(\frac{1}{7}-\frac{1}{10})...(\frac{1}{3n-2}-\frac{1}{3n+1})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd762211b6cbe3cd5071092fb9e05c65_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{3}\left[1-\frac{1}{3n+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bd1c21e3c8f00eb3511df6f93f01ee5f_l3.png)
= 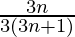
= 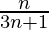
Therefore, sum of the given series up to n terms is 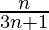 .
.
Question 10. 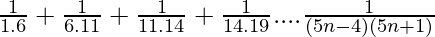 to n terms.
to n terms.
Solution:
We are given the nth term of the given series,
an = 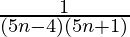
= ![Rendered by QuickLaTeX.com \frac{1}{5}\left[\frac{1}{5n-4}-\frac{1}{5n+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-025a3f95ba2c834f209fe0af058ecb2e_l3.png)
Now we have to summate our nth term to find the sum(Sn) of this series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n} a_k = \frac{1}{5}\sum_{k=1}^{n} \left[\frac{1}{5n-4}-\frac{1}{5n+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b9997e8911fbb9cd75607c140aa32ebd_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{3}\left[(1-\frac{1}{6})+(\frac{1}{6}-\frac{1}{11})+(\frac{1}{11}-\frac{1}{14})...(\frac{1}{5n-4}-\frac{1}{5n+1})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0062adc73559e9ec133455089d87d47c_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{5}\left[1-\frac{1}{5n+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e711a8c78a9201b020fa0d523cc1dcb_l3.png)
= 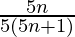
= 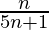
Therefore, sum of the given series up to n terms is 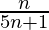 .
.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...