Class 11 RD Sharma Solutions – Chapter 21 Some Special Series- Exercise 21.1
Last Updated :
18 Mar, 2021
Find the sum of the following series to n terms.(Question 1-5)
Question 1. 13 + 33 + 53 + 73 + ……
Solution:
Let us assume Tn to be the nth term of the given series.
Now, we have:
Tn = [1 + (n – 1)2]3
= (2n – 1)3
= (2n)3 – 3 (2n)2. 1 + 3.12.2n – 13 [Since, (a – b)3 = a3 – 3a2b + 3ab2 – b]
= 8n3 – 12n2 + 6n – 1
Also, let us assume Sn to be the sum of n terms of the given series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n T_k \\ = \sum_{k=1}^n [2k-1]^3 \\ = \sum_{k=1}^n [8k^3 - 1 - 6k(2k-1)] \\ = \sum_{k=1}^n [8k^3 - 1 - 12k^2 + 6k] \\ = 8 \sum_{k=1}^n k^3 - \sum_{k=1}^n 1 - 12 \sum_{k=1}^n k^2 + 6 \sum_{k=1}^n k \\ = \frac{8n^2(n+1)^2}{4} - n - \frac{12n(n+1)(2n+1)}{6} + \frac{6n(n+1)}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b3f404061890d676387f430dba3ff0b_l3.png)
Simplifying the equation we get
= 2n2 (n + 1)2 – n – 2n (n + 1) (2n + 1) + 3n (n + 1)
= n (n + 1) [2n (n + 1) – 2 (2n + 1) + 3] – n
= n (n + 1) [2n2 – 2n + 1] – n
= n [2n3 – 2n2 + n + 2n2 – 2n + 1 – 1]
= n [2n3 – n]
= n2 [2n2 – 1]
Therefore,
The sum of the series is n2 [2n2 – 1].
Question 2. 23 + 43 + 63 + 83 + ………
Solution:
Let us assume Tn to be the nth term of the given series.
Now, we have:
Tn = (2n)3
= 8n3
Also, let us assume Sn to be the sum of n terms of the given series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n 8k^3 \\ = 8 \sum_{k=1}^n k^3 \\ = 8[\frac{n(n+1)}{2}]^2 \\ = 8 * \frac{n^2(n+1)^2}{4} \\ = 2n^2(n+1)^2 \\ = 2{n(n+1)}^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d182ae7c8f18172ae141707b3c0089c_l3.png)
Therefore,
The sum of the given series is 2{n (n + 1)}2
Question 3. 1.2.5 + 2.3.6 + 3.4.7 + ……
Solution:
Let us assume Tn to be the nth term of the given series.
Now, we have:
Tn = n (n + 1) (n + 4)
= n (n2 + 5n + 4)
= n3 + 5n2 + 4n
Also, let us assume Sn to be the sum of n terms of the given series.
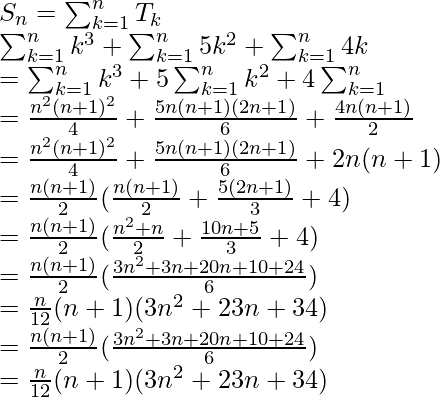
Therefore,
The sum of the given series is 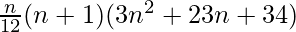
Question 4. 1.2.4 + 2.3.7 + 3.4.10 + ….
Solution:
Let us assume Tn to be the nth term of the given series.
Now, we have:
Tn = n (n + 1) (3n + 1)
= n (3n2 + 4n + 1)
= 3n3 + 4n2 + n
Also, let us assume Sn to be the sum of n terms of the given series.
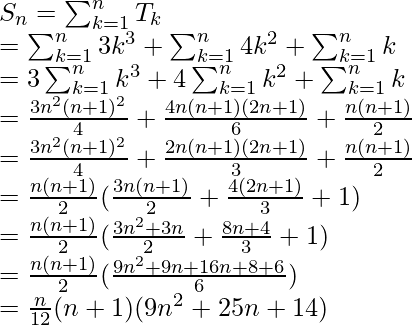
Therefore,
The sum of the given series is 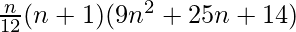
Question 5. 1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4) + …
Solution:
Let us assume Tn to be the nth term of the given series.
Now, we have:
Tn = n(n + 1)/2
= (n2 + n)/2
Also, let us assume Sn to be the sum of n terms of the given series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n T_k \\ = \sum_{k=1}^n (\frac{k^2+k}{2}) \\ = 1/2 \sum_{k=1}^n (k^2+k) \\ = 1/2 [\frac{n(n+1)(2n+1)}{6} + \frac{n(n+1)}{2} ] \\ = \frac{n(n+1)}{4}(\frac{2n+1}{3} + 1) \\ = \frac{n(n+1)}{4} (\frac{2n+4}{3}) \\ = \frac{n(n+1)(2n+4)}{12} \\ = \frac{n(n+1)(n+2)}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-59256d777eca7d108eb458320e76be62_l3.png)
Therefore,
The sum of the series is [n(n + 1)(n + 2)]/6
Question 6. Find the sum of the series 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + … upto n terms.
Solution:
Let us assume Tn to be the nth term of the given series.
Tn = (nth term of 1, 2, 3..) x (nth term of 2, 3, 4…)
= [1 + (n + 1) x 1].[2 + (n + 1) x 1]
= [1 + n – 1].[2 + n – 1]
= n(n + 1)
= n2 + n
Also, let us assume Sn to be the sum of n terms of the given series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n T_n \\ = \sum_{k=1}^n (n^2 + n) \\ = \frac{n(n+1)(2n+1)}{6} + \frac{n(n+1)}{2} \\ = \frac{n(n+1)(2n+1)+3n(n+1)}{6} \\ = \frac{n(n+1)[2n+1+3]}{6} \\ = \frac{n(n+1)[2n+4]}{6} \\ = \frac{n(n+1) x 2 (n+2)}{6} \\ = \frac{n}{6} (n+1)(n+2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85fc5b50339656f765a9ed652458e88f_l3.png)
Question 7. Find the sum of the series 3 × 12 + 5 × 22 + 7 × 32 + … upto n terms.
Solution:
Let us assume Tn to be the nth term of the given series.
Tn = (nth term of 3, 5, 7..) x (nth term of 12, 22, 32…)
= [3 + (n – 1) x 2].[n2]
= [2n + 1]. [n2]
= 2n3 + n2
Tn = 2n3 + n2
Also, let us assume Sn to be the sum of n terms of the given series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^n T_n \\ = \sum_{k=1}^n (2n^3 + n^2) \\ = \sum_{k=1}^n 2n^3 + \sum_{k=1}^n n^2 \\ = 2 \sum_{k=1}^n n^3 + \sum_{k=1}^nn^2 \\ = 2[\frac{n(n+1)}{2}]^2 + [\frac{n(n+1)(2n+1)}{6}] \\ = \frac{2}{4}[n(n+1)]^2 + \frac{n(n+1)(2n+1)}{6} \\ = [\frac{n(n+1)}{2}]^2 + \frac{n(n+1)(2n+1)}{6} \\ = \frac{n(n+1)}{6}[3n(n+1)+(2n+1)] \\ = \frac{n(n+1)}{6}[3n^2+3n+2n+1] \\ \frac{n}{6}(n+1)(3n^2+5n+1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb6444b5dabe0172475f1ee0076e02db_l3.png)
Therefore,
The sum of the series = 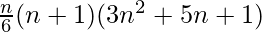
Question 8 (i). Find the sum of the series 2n3 + 3n2 – 1 to n terms.
Solution:
Tn = 2n3 + 3n2 – 1
Also, let us assume Sn to be the sum of n terms of the given series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n}T_k \\ = 2 \sum_{k=1}^{n} 2k^3+ \sum_{k=1}^{n}3k^2 - \sum_{k=1}^{n} 1 \\ = 2[\frac{n(n+1)}{2}]^2 + 3[\frac{n(n+1)(2n+1)}{6}] -n \\ = \frac{2}{4}[n(n+1)]^2 + \frac{n(n+1)(2n+1) - n }{2} \\ = \frac{[n(n+1]^2+n(n+1)(2n+1)-n}{2} \\ = \frac{n}{2}[n(n+1)^2 + (n+1)(2n+1) - 2] \\ = \frac{n}{2} [n^3+n+2n^2+2n^2+3n-1] \\ = \frac{n}{2} [n^3+4n^2+4n-1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05eacf14c561329762511541be707d5a_l3.png)
Sum of n terms = ![Rendered by QuickLaTeX.com \frac{n}{2} [n^3+4n^2+4n-1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c21485d5377a47ef1bd9ffe279d916b_l3.png)
Question 8 (ii). Find the sum of the series n3 – 3n to n terms.
Solution:
Tn = n3 – 3n
Also, let us assume Sn to be the sum of n terms of the given series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n}T_k \\ = \sum_{k=1}^{n}(k^3-3^k) \\ = \sum_{k=1}^{n} k^3 - \sum_{k=1}^{n} 3^k \\ = [\frac{n(n+1)}{2}]^2-(3^1+3^2+...+3^n) \\ = \frac{n^2(n+1)^2}{4}-3\frac{3^n-1}{3-1} \\ = \frac{n^2(n+1)^2}{4}-\frac{3}{2}(3^n-1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7affa9d38d0325b9ca339c10ac5d5846_l3.png)
Question 8 (iii). Find the sum of the series n(n + 1)(n + 4) to n terms.
Solution:
Tn = n(n + 1)(n + 4)
Also, let us assume Sn to be the sum of n terms of the given series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n}T_k \\ = \sum_{k=1}^{n}(k^3+5k^2+4k) \\ = \sum_{k=1}^{n} k^3 + \sum_{k=1}^{n} 5k^2 + \sum_{k=1}^{n} 4k \\ = \sum_{k=1}^{n} k^3 + 5 \sum_{k=1}^{n} k^2 + 4 \sum_{k=1}^{n}k \\ = [\frac{n(n+1)}{2}]^2 + 5[\frac{n(n+10(2n+1)}{6}]+\frac{4n(n+1)}{2} \\ = \frac{1}{4}[n(n+1)]^2 + \frac{5n(n+1)(2n+1}{6}+2n(n+1) \\ = \frac{3[n(n+1)]^2+10n(n+1)(2n+1)+24n(n+1)}{12} \\ = \frac{n(n+1)}{12}[3n(n+1)+10(2n+1)+24] \\ = \frac{n(n+1)}{12}[3n^2+23n+34]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e0422fa33ec900ae68b7cfa1e7f50b85_l3.png)
Question 8 (iv). Find the sum of the series (2n – 1)2 to n terms.
Solution:
Tn = (2n – 1)2
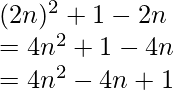
Also, let us assume Sn to be the sum of n terms of the given series.
![Rendered by QuickLaTeX.com S_n = \sum_{k=1}^{n}T_k \\ = \sum_{k=1}^{n}4k +\sum_{k=1}^{n}1 \\ = \sum_{k=1}^{n}k^2 -4\sum_{k=1}^{n}k + \sum_{k=1}^{n}1 \\ = 4[\frac{n(n+1)(2n+1)}{6}]-4\frac{n(n+1)}{2}+n \\ = 2/3n(n+1)(2n+1)-2n(n+1)+n \\ = \frac{2}{3}n(n+1)(2n+1)-2n^2-2n+n \\ = \frac{2n}{3}(n+1)(2n+1) - n(2n+1) \\ = \frac{n}{3} (2n+1)[2(n+1)-3] \\ = \frac{n}{3}(2n+1)(2n+2-3) \\ = \frac{n}{3}(2n+1)(2n-1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43593d44f7b3dc8c640087fd228dc708_l3.png)
Question 9. Find the 20th term and the sum of 20 terms of the series 2 × 4 + 4 × 6 + 6 × 8 +…..
Solution:
Let us assume Tn to be the nth term of the given series.
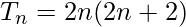
The 20th term of the series is :
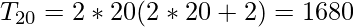
The infinite series is equivalent to,
2 × 4 + 4 × 6 + 6 × 8 + …. = 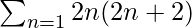
Sum of the series until 20th term is equivalent to
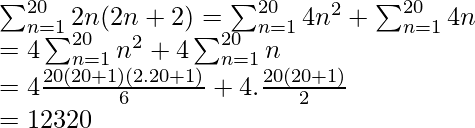
Share your thoughts in the comments
Please Login to comment...