Question 1: Insert 6 geometric means between 27 and 1/81.
Solution:
Let the six geometric means be A1, A2, A3, A4, A5, A6.
Now, these 6 terms are to be added between 27 and 1/81.
So the G.P. becomes, 27, A1, A2, A3, A4, A5, A6,1/81 with first term(a) = 27, number of terms(n) = 8 and 8th term(a8) = 1/81.
We know nth term of a G.P. is given by an = arn-1, where r is the common ratio.
=> a8 = 1/81
=> 27(r)8-1 = 1/81
=> r7 = 1/(81×27)
=> r7 = (1/3)7
=> r = 1/3
So, geometric means are:
A1 = ar = 27(1/3) = 9
A2 = ar2 = 27(1/3)2 = 3
A3 = ar3 = 27(1/3)3 = 1
A4 = ar4 = 27(1/3)4 = 1/3
A5 = ar5 = 27(1/3)5 = 1/9
A6 = ar6 = 27(1/3)6 = 1/27
Therefore, the 6 geometric means between 27 and 1/81 are 9, 3, 1, 1/3, 1/9, 1/27.
Question 2. Insert 5 geometric means between 16 and 1/4.
Solution:
Let the five geometric means be A1, A2, A3, A4, A5.
Now, these 5 terms are to be added between 16 and 1/4.
So the G.P. becomes, 16, A1, A2, A3, A4, A5,1/4 with first term(a) = 16, number of terms(n) = 7 and 7th term(a7) = 1/4.
We know nth term of a G.P. is given by an = arn-1, where r is the common ratio.
=> a7 = 1/4
=> 16(r7-1) = 1/4
=> r6 = 1/64
=> r6 = (1/2)6
=> r = 1/2
So, geometric means are:
A1 = ar = 16(1/2) = 8
A2 = ar2 = 16(1/2)2 = 4
A3 = ar3 = 16(1/2)3 = 2
A4 = ar4 = 16(1/2)4 = 1
A5 = ar5 = 16(1/2)5 = 1/2
Therefore, the 5 geometric means between 16 and 1/4 are 8, 4, 2, 1, 1/2.
Question 3. Insert 5 geometric means between 32/9 and 81/2.
Solution:
Let the five geometric means be A1, A2, A3, A4, A5.
Now, these 5 terms are to be added between 32/9 and 81/2.
So the G.P. becomes, 32/9, A1, A2, A3, A4, A5, 81/2 with first term(a) = 32/9, number of terms(n) = 7 and 7th term(a7) = 81/2.
We know nth term of a G.P. is given by an = arn-1, where r is the common ratio.
=> a7 = 81/2
=> (32/9)(r7-1) = 81/2
=> r6 = (81×9)/(2×32)
=> r6 = (3/2)6
=> r = 3/2
So, geometric means are:
A1 = ar = (32/9)×(3/2) = 16/3
A2 = ar2 = (32/9)×(3/2)2 = 8
A3 = ar3 = (32/9)×(3/2)3 = 12
A4 = ar4 = (32/9)×(3/2)4 = 18
A5 = ar5 = (32/9)×(3/2)5 = 27
Therefore, the 5 geometric means between 32/9 and 81/2 are 16/3, 8, 12, 18, 27.
Question 4. Find the geometric means of the following pairs of numbers:
(i) 2 and 8
(ii) a3b and ab3
(iii) –8 and –2
Solution:
We know geometric mean between two numbers, a and b is given by 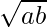 .
.
(i) 2 and 8
Here, a = 2 and b = 8
So, G.M. = 
= 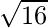
= 4
(ii) a3b and ab3
Here, a = a3b and b = ab3
So, G.M. = 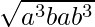
= 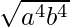
= a2b2
(iii) –8 and –2
Here, a = –8 and b = –2
G.M. = 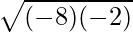
= 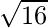
= 4
Question 5. If a is the G.M. of 2 and 1/4 find a.
Solution:
We know geometric mean between two numbers, a and b is given by 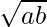 .
.
According to the question,
a = 
= 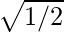
= 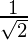
Therefore, the value of a is 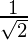 .
.
Question 6. Find the two numbers whose A.M. is 25 and GM is 20.
Solution:
We know geometric mean between two numbers, a and b is given by 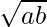 and arithmetic mean between two numbers, a and b is given by (a+b)/2.
and arithmetic mean between two numbers, a and b is given by (a+b)/2.
According to the question,
=> 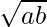 = 20 ……. (1)
= 20 ……. (1)
And
=> (a+b)/2 = 25
=> a+b = 50
=> b = 50–a ……. (2)
From (1) and (2), we get,
=> 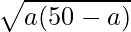 = 20
= 20
Squaring both sides, we get,
=> a(50 –a) = 400
=> a2 – 50a + 400 = 0
=> a2– 40a–10a+400 = 0
=> a(a– 40) – 10(a– 40) = 0
=> (a– 40) (a– 10) = 0
=> a = 40 or a = 10
Putting these in (2) we get,
When a = 40, then b = 10 and
When a = 10, then b = 40.
Therefore, the numbers are 10 and 40.
Question 7. Construct a quadratic in x such that A.M. of its roots is A and G.M. is G.
Solution:
Suppose the roots of the quadratic equation are a and b.
We know geometric mean between two numbers, a and b is given by 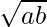 and arithmetic mean between two numbers, a and b is given by (a+b)/2.
and arithmetic mean between two numbers, a and b is given by (a+b)/2.
According to the question,
A.M. of roots = (a+b)/2 = A
a + b = 2A ….. (1)
And G.M. of roots = 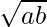 = G
= G
ab = G2 … (2)
Now, we know a quadratic equation in x with roots a and b is given by,
x2 – (a+b)x + (ab) = 0
From (1) and (2), we get,
x2 – 2Ax + G2 = 0
Therefore, the required quadratic equation is x2 – 2Ax + G2 = 0.
Question 8. The sum of two numbers is 6 times their geometric means. Show that the numbers are in the ratio 
Solution:
Let the two numbers be a and b. We know geometric mean between two numbers, a and b is given by ![Rendered by QuickLaTeX.com \sqrt[]{ab}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ba7ae5ea555faedf4c42379c6981e7fd_l3.png) .
.
According to the question,
=> a+b = 6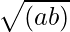
=> 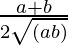 =
= 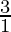
Applying Componendo and Dividendo on both sides, we get,
=> 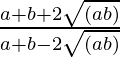 =
= 
=> ![Rendered by QuickLaTeX.com \left[\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b55c23399d7746430c9f718eb5a5747_l3.png) =
= 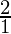
=> 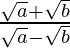 =
= 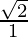
By again applying Componendo and Dividendo on both sides, we get,
=> 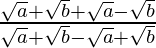 =
= 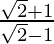
=> 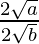 =
= 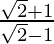
=> 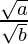 =
= 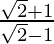
Squaring both sides, we get
=> 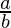 =
= ![Rendered by QuickLaTeX.com \left[\frac{\sqrt{2}+1}{\sqrt{2}-1}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e234eb96ade88cc98c5c248e525ba8a8_l3.png)
=> 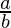 =
= 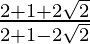
=> 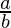 =
= 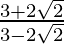
Hence proved.
Question 9. If AM and GM of roots of a quadratic equation are 8 and 5 respectively, then obtain the quadratic equation.
Solution:
Suppose the roots of the quadratic equation are a and b.
We know geometric mean between two numbers, a and b is given by 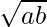 and arithmetic mean between two numbers, a and b is given by (a+b)/2.
and arithmetic mean between two numbers, a and b is given by (a+b)/2.
According to the question,
A.M. of roots = (a+b)/2 = 8
a+b = 16 ….. (1)
And G.M. of roots = 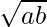 = 5
= 5
ab = 25 .… (2)
Now, let the quadratic equation with roots a and b is given by,
x2 – (a+b)x + (ab) = 0
From (1) and (2), we get,
x2 – 16x + 25 = 0
Therefore, the required quadratic equation is x2 – 16x + 25 = 0.
Question 10. If AM and GM of the two positive numbers a and b are 10 and 8 respectively. Find the numbers.
Solution:
We know geometric mean between two numbers, a and b is given by 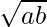 and arithmetic mean between two numbers, a and b is given by (a+b)/2.
and arithmetic mean between two numbers, a and b is given by (a+b)/2.
According to the question,
=> 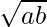 = 8 ……. (1)
= 8 ……. (1)
And,
=> (a+b)/2 = 10
=> a+b = 20
=> b = 20–a ……. (2)
From (1) and (2), we get,
=> 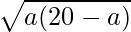 = 8
= 8
Squaring both sides, we get,
=> a(20–a) = 64
=> a2–20a+64 = 0
=> a2–16a–4a+64 = 0
=> a(a–16) – 4(a–16) = 0
=> (a–4) (a–16) = 0
=> a = 4 or a = 16
Putting a = 4 in (2), we get b = 16. And,
Putting a = 16 in (2), we get b = 4.
Therefore, the numbers are 4 and 16.
Question 11. Prove that the product of n geometric means between two quantities is equal to the nth power of geometric mean of those two quantities.
Solution:
Suppose we have a GP with first term a, common ratio r and number of terms n.
We have to add these n terms of GP between two quantities such that the GP remains maintained. So total number of terms become (n+2).
We know nth term of a G.P. is given by an = arn-1.
So, the last term of the GP ,i.e., (n+2)th term will be, an+2 = arn+2-1 = arn+1
We know geometric mean between two numbers, a and b is given by 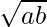 .
.
The GM of a and arn+1 will be, G1 = 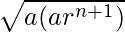 =
= 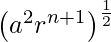
Hence, L.H.S. = 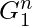 =
= 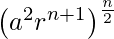
Now, R.H.S. = Product of n geometric means between these two quantities, G2 = ar × ar2 × . . . . × arn
= 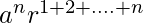
= 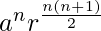
= ![Rendered by QuickLaTeX.com \left[a^2r^{n+1}\right]^{\frac{n}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc874ca5679b308a29d225d357678a54_l3.png)
= 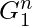
= L.H.S.
Hence, Proved.
Question 12: If the AM of two positive numbers a and b (a>b) is twice their geometric mean. Prove that a:b = 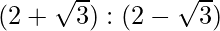
Solution:
We know geometric mean between two numbers, a and b is given by 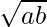 and arithmetic mean between two numbers, a and b is given by (a+b)/2.
and arithmetic mean between two numbers, a and b is given by (a+b)/2.
According to the question,
AM = 2(GM)
=> 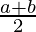 =
= 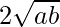
=> 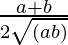 =
= 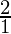
Applying Componendo and Dividendo on both sides, we get,
=> 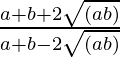 =
= 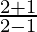
=> ![Rendered by QuickLaTeX.com \left[\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b55c23399d7746430c9f718eb5a5747_l3.png) =
= 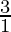
=> 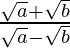 =
= 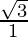
By again applying Componendo and Dividendo on both sides, we get,
=> 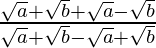 =
= 
=> 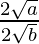 =
= 
=> 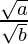 =
= 
Squaring both sides, we get
=> 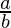 =
= ![Rendered by QuickLaTeX.com \left[\frac{\sqrt{3}+1}{\sqrt{3}-1}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9dba7f32fb739220c4c77329e056f99f_l3.png)
=> 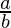 =
= 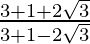
=> 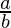 =
= 
=> 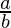 =
= 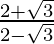
Hence, proved.
Question 13. If one AM, A, and two geometric means G1 and G2 are inserted between any two positive numbers, show that 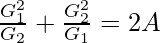
Solution:
Let the two positive numbers be a and b.
Now value of one AM between a and b, A = (a+b)/2.
So, 2A = a+b . . . . (1)
If we add two geometric means between a and b, the GP becomes a,G1,G2,b.
Now, we know b = ar4-1, where r is the common ratio.
=> r3 = 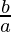
=> r = ![Rendered by QuickLaTeX.com \left[\frac{b}{a}\right]^{\frac{1}{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a161dd02844f764eba9ec4c6f360a76b_l3.png)
So, G1 = ar = ![Rendered by QuickLaTeX.com a\left[\frac{b}{a}\right]^{\frac{1}{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4f489ec598ae21253a493facb14a2925_l3.png) =
= 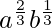
G2 = ar2 = ![Rendered by QuickLaTeX.com a\left[\frac{b}{a}\right]^{\frac{2}{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1237d963806b31d5ad49fb75ed2b9d0c_l3.png) =
= 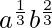
Now, L.H.S. = 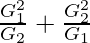
= 
= ab0 + a0b
= a+b
= 2A [From (1)]
= R.H.S.
Hence, proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...