Class 11 RD Sharma Solutions – Chapter 19 Arithmetic Progressions- Exercise 19.7 | Set 2
Last Updated :
13 Jan, 2021
Question 11. A man starts repaying a loan as first installment of Rs. 100. If he increases the installment by Rs. 5 every month, what amount he will pay in the 30th installment?
Solution:
In the first installment, the man pays Rs. 100, so a1 = 100 and in next installment the man pays Rs. 105, so a2 = 105.
So we can conclude, common difference, d = 105 – 100 = 5
Thus, the money he will pay in 30th installment, a30 = a1 + 29d = 100 + 29 x 5 = 100 + 145 = 245
Hence, he will pay Rs. 245 in the 30th installment.
Question 12. A carpenter was hired to build 192 window frames. The first day he made five frames and each day thereafter he made two more frames than he made the day before. How many did it take him to finish the job?
Solution:
On the first day, the carpenter makes 5 frames, so a = 5 and thereafter each day he makes 2 extra frames, so d = 2.
Total frames to be made, Sn = 192
We know the formula,
![Rendered by QuickLaTeX.com S_n = \frac{n[2a + (n-1)d]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e81d2d04f14c3b4f1d8d16db8842af49_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow 192 = \frac{n[2\times 5 + (n-1)2]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f698515057acad4e883ebe99b12382e5_l3.png)
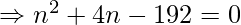
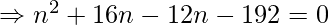
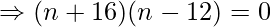
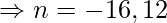
We will neglect n= -16 and consider n = 12
Therefore, the carpenter took 12 days to make 192 frames.
Question 13. We know that the sum of interior angled of a triangle is 180°. Show that the sums of the interior angles of polygons with 3,4,5,6…. form an arithmetic progression. Find the sum of the interior angles for a 21 sided polygon.
Solution:
The sum of interior angles of a polygon having n-sides is = (n-2) x 180°
Thus, for a polygon with 3 sides, we have a3 = (3-2) x 180° = 180°
similarly, for a polygon with 4 sides, we have a4 = (4-2) x 180° = 360°
for a triangle with 5 sides, we have a5 = (5-2) x 180° = 540°
Now, a4 – a3 = 360° – 180° = 180°
also, a5 – a4 = 540° – 360° = 180°, we are getting the same common difference for every succeeding and preceding term, hence we can say that it forms an AP.
Now, the sum of the interior angles for a 21 sided polygon = (21-2) x 180° = 3420°
Question 14. In a potato race 20 potatoes are placed in a line at intervals of 4 m with the first potato 24 m from the starting point. A contestant is required to bring the potatoes back to the starting place one at a time. How far would he run in bringing back all the potatoes?
Solution:
Since, there are in total 20 potatoes and they are placed in a line at intervals of 4 m, therefore. n = 20 and d=4
First potato is placed at a distance of 24 m, so a1 = 24, now a2 = 28, similarly a20 = 24+ 19 x 4 = 100.
We know the formula, ![Rendered by QuickLaTeX.com S_n = \frac{n}{2}\left [ a+l \right ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6faa253067639eabdd8546c89093feef_l3.png)
therefore, ![Rendered by QuickLaTeX.com S_n = \frac{20}{2}\left [ 24 + 100 \right ] = 1240](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87187feac37bcc9bb37ccacde97b1a34_l3.png)
The contestant has to bring back the potatoes hence, he will run back and forth, so total distance covered = 1240 x 2 =2480 m.
Question 15. A man accepts a position with an initial salary of Rs. 5200 per month. It is understood that he will receive an automatic increase of Rs. 320 in the very next month and each month thereafter.
(i) Find his salary for the tenth month.
(ii) What is total earnings during the first year?
Solution:
Given: initial salary, a = Rs. 5200 and d = Rs. 320.
(i) his salary in 10th month = a + 9d = 5200 + 9 x 320 = 8080
(ii) his total earnings during the first year
![Rendered by QuickLaTeX.com = \frac{12}{2}\left [ 2 \times 5200 + (12-1)\times 320 \right ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-612dba6d790f4f108c0248784377cd1b_l3.png)
![Rendered by QuickLaTeX.com 6\left [ 10400 + 3520 \right ] = 6 \times 13920 = 83520](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4f1297a9bcb0d61ff7103980e1345c29_l3.png)
Question 16. A man saved Rs. 66000 in 20 years. In each succeeding year after the first year he saved Rs. 200 more than what he saved in the previous year. How much did he save in the first year?
Solution:
Given: Sn = 66000, n=20, d=200.
We know the formula,
![Rendered by QuickLaTeX.com S_n = \frac{n[2a + (n-1)d]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e81d2d04f14c3b4f1d8d16db8842af49_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow 66000 = \frac{20[2\times a + (20-1)200]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8af2130c44d378f9a0e6bcfe99a29e57_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow 66000 = 10[2\times a + 19\times 200]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9906c05428329f5a4af1bf507bfee411_l3.png)

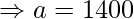
The man saved Rs. 1400 in the first year.
Question 17. In a cricket team tournament 16 teams participated. A sum of Rs 8000 is to be awarded among themselves as prize money. If the last place team is awarded Rs 275 in prize money and the award increases by the same amount for successive finishing places, how much amount will the first place team receive?
Solution:
Total number of teams participating in the tournament, n = 16
Total prize money, Sn = 8000
The last placed team received prize money, a = 275
Suppose, for every successive team the prize money increases by d, then by the sum formula
![Rendered by QuickLaTeX.com \Rightarrow 8000 = \frac{16[2\times 275 + (16-1)d ]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9c92e4b3b41f1565f4275be8c453ced2_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow 1000 = [550 + 15d ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ebc7a87469629471bfaf653b6f822b0b_l3.png)
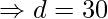
therefore, the amount received by the first placed team = a+15d = 275 + 15 x 30 = 725
Hence, the first placed team received Rs 725 as the prize money.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...