Question 1. In how many ways can the letters of the word ‘FAILURE’ be arranged so that the consonants may occupy only odd positions?
Solution:
From the given word, we get
F, L, R = 3 consonants
A, I, U, E = 4 vowels
1, 3, 5, 7 = 4 odd positions possible
Out of these 4 positions select 3 positions for the 3 given consonants = 4P3 = 4 ways
Now for these positions, ways to arrange consonants = 3! = 6
And ways to arrange the vowels in remaining positions are = 4! = 24
Total ways = 4 x 6 x 24 = 576
Question 2. In how many ways can the letters of the word ‘STRANGE’ be arranged so that
(i) The vowels come together?
(ii) The vowels never come together? And
(iii) The vowels occupy only the odd places?
Solution:
(i) 2 vowels are given, for these to be together let the first of two vowels occupy a position p
Now, there are 6 ways in which p can be chosen.
(All 7 positions except the last position, because if the first vowel
comes at the last position, no position will be left there for the second vowel)
For each p chosen, the vowels can be put in two orders (AE, EA) = 2 ways
Remaining letters can be arranged in = 5! = 120 ways
Total ways = Ways of choosing positions for vowels x
Ways to arrange the vowels x
Ways to arrange the remaining letters
= 6 x 2 x 120 = 1440
(ii) Let the first vowel be at position p.
p can be chosen in 6 different ways (1 to 6).
When first vowel is at p, then second can be from p+2 to 7 so that not consecutive.
= 7 – (p + 2) + 1 = (6 – p)ways
Case 1 : p = 1 ⇒ 6 – p = 5
Case 2: p=2 ⇒ 6 – p = 4
and so on till 6 – p = 0 for Case 6.
No. of ways of selecting vowels positions in the word = 5 + 4 + 3 + 2 + 1 + 0 = 15
For each selection, ways to put the vowels = 2 (AE and EA)
Ways of putting the remaining letters = 5! = 120
Total ways = 15 x 2 x 120 = 3600
(iii) Choosing 2 odd positions from 4 = 4P2 = 4 x 3 / 2 = 6
Ways of arranging two vowels in selected positions = 2! = 2
Ways of arranging other letters are = 5! = 120
Total ways = 6 x 2 x 120 = 1440
Question 3. How many words can be formed from the letters of the word ‘SUNDAY’? How many of these begin with D?
Solution:
Total number of letters present in the given word = 6
So, ways to arrange 6 letters to get the words = 6! = 720
Now, when D is fixed at position 1, remaining 5 can be arranged in ways = 5! = 120
Question 4. How many words can be formed out of the letters of the word, ‘ORIENTAL,’ so that the vowels always occupy the odd places?
Solution:
From the given word, we get 4 vowels and 4 odd positions possible (1, 3, 5, 7)
So, the ways to arrange the vowels = 4! = 24
Ways to arrange consonant letters = 4! = 24
Total ways = 24 x 24 = 576
Question 5. How many different words can be formed with the letters of word ‘SUNDAY’? How many of the words begin with N? How many begin with N and end in Y?
Solution:
Total number of letters present in the given word = 6
Now, Ways to arrange the 6 letters to get the words = 6! = 720
So now we find how many words begin with N
Let the fix N on the first position and remaining letter is 5
So the arrangement of 5 letters can be in 5! ways = 120 ways
Now find how many begin with N and end in Y
Let fix Y at position number 6 and N at position number 1 and the remaining letter is 4
So, the arrangement of 4 letters can be in 4! ways = 24 ways
Question 6. How many different words can be formed from the letters of the word ‘GANESHPURI’? In how many of these words:
(i) The letter G always occupies the first place?
(ii) The letter P and I respectively occupy the first and last place?
(iii) Are the vowels always together?
(iv) The vowels always occupy even places?
Solution:
Given: Total number of letters present in the given word = 10
(i) Fix G at position number 1 and the remaining letters are 9
So, the remaining letters can be arranged 9! = 51840 ways
(ii) The letter P and I respectively occupy the first and last place and the remaining letters are 8
So, the remaining letters can be arranged 8! = 5760 ways
(iii) Total number of vowels present = 4
The first vowel can be at max at position 7 (otherwise remaining vowels would
not have enough required positions)
So from 1 to 7 positions first vowel can be put at 7P1 = 7 ways
Remaining will be put in next consecutive positions in the word. (so 1 way)
Ways to select the vowels positions = Ways to put first vowel x Ways to put remaining vowels
= 7 x 1 = 7 ways
Ways to arrange the 4 vowels in these 4 selected positions = 4! = 24 ways
Ways to arrange the consonant letters will be = 6! = 720 ways
Total words having vowels always together = Ways to choose the vowels positions x
Ways to arrange vowels x
Ways to arrange consonants
= 7 x 24 x 720
= 120960
(iv) 5 positions possible that are even (2, 4, 6, 8, 10)
We have 4 vowels and need to choose 4 even positions = 5P4 = 5 ways
Ways to arrange these 4 vowels = 4! = 24
Ways to arrange the 6 consonants = 6! = 720
Total words = 5 x 24 x 720
= 86400
Question 7. How many permutations can be formed by the letters of the word, ‘VOWELS’, when
(i) There is no restriction on letters?
(ii) Each word begins with E?
(iii) Each word begins with O and ends with L?
(iv) All vowels come together?
(v) All consonants come together?
Solution:
Given: Total number of letters = 6
(i) Ways to arrange 6 letters are = 6! = 720
(ii) Fix E at first position and the remaining letters are 5
So, the remaining letters can be arranged = 5! = 120 ways
(iii) Fix O at 1st and L at last position. So the remaining 4 letters
These 4 letters can be arranged = 4! = 24 ways
(iv) 2 vowels together can consider them 1 symbol = 2 ways for this new symbol (EO and OE)
1 symbol and 4 letters = 5 things are to be arranged so number of ways = 5! =120
Total ways = 120 x 2 = 240
(v) Consonants together = VWLS are 1 group = 4! ways
Group of consonants and 2 vowels = 3 things = 3! ways to arrange
Total ways = 4! x 3! = 144
Question 8. How many words can be formed out of the letters of the word ‘ARTICLE’, so that vowels occupy even places?
Solution:
In the given word, we have 3 vowels and also 3 even positions there
So 3! ways to occupy places for vowels.
For consonants = 4! = 24 ways
Total words = 3! x 4! = 144
Question 9. In how many ways can a lawn tennis mixed double be made up from seven married couples if no husband and wife play in the same set?
Solution:
2 teams with 1 man and 1 woman
Need to select 2 man so number of ways are = 7P2 = 21
Need to select 2 woman out of 5 (except wives of selected men), ways = 5 P2 = 10
Now, ways to assign teams to men are = 2 (1st man to team A or to team B)
Similarly, for women too = 2 ways
Number of required ways = 21 x 10 x 2 x 2 = 840
Question 10. m men and n women are to be seated in a row so that no two women sit together. If m>n then show that the number of ways in which they can be seated as 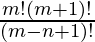
Solution:
Let us first seat the men = m! ways
Now, m+1 spaces are created for women tor sit.
(before 1st man, between two consecutive men, after last seated man)
Out of these m+1 spaces, we need to choose n spaces for the women = m+1Pn possible ways
Arrange women in n! ways after selecting seats for them above.
Total ways to seat = m! x n! x (m+1)! / ( (m + 1 – n!) x n! )
= m! (m+1)! / (m+1-n)!
Hence, shown.
Question 11. How many words (with or without dictionary meaning) can be made from the letters in the word MONDAY, assuming that no letter is repeated, if
(i) 4 letters are used at a time?
(ii) All letters are used at a time?
(iii) All letters are used but first is vowel?
Solution:
(i) Select 4 letters out of 6 = 6P4 = 6 x 5 / 2 = 15
Ways to arrange these = 4! = 24
Total such words possible = 15 x 24 = 360
(ii) Number of such words = 6! = 720
(iii) Possibilities for first position = 2 (O or A)
Number of arrangements for other positions in the word are = 5!
Total words = 2 x 5! = 240
Question 12. How many three-letter words can be made using the letters of the word ‘ORIENTAL’?
Solution:
Total number of the letters present in the given word = 4
Select 3 letters out of 8 = 8P3 = 56 ways
We have 3! ways to arrange
Hence, the total words = 56 x 3! = 336
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...