Question 1. Find the modulus and argument of the following complex numbers and hence express each of them in the polar form:
(i) 1 + i
(ii) √3 + i
(iii) 1 – i
(iv) (1 – i)/(1 + i)
(v) 1/(1 + i)
(vi) (1 + 2i)/(1 – 3i)
(vii) sin 120o – i cos 120o
(viii) –16/(1 + i√3)
The polar form of a complex number Z = x + iy is given by Z = |Z| (cos θ + i sin θ) where,
Modulus of complex number, |Z| = √(x2 + y2)
Argument of complex number, θ = arg (Z) = tan–1 (y/x)
(i) 1 + i
Solution:
We are given, Z = 1 + i, so x = 1 and y = 1.
|Z| = √(12 + 12) = √2
θ = tan-1 (1/1) = tan-1 1
As x > 0 and y > 0, Z lies in 1st quadrant and the value of θ is 0 ≤ θ ≤ π/2.
So, θ = π/4 and Z = √2 (cos (π/4) + i sin (π/4))
Therefore, the polar form of (1 + i) is √2 (cos (π/4) + i sin (π/4)).
(ii) √3 + i
Solution:
We are given, Z = √3 + i, so x = √3 and y = 1.
|Z| = √((√3)2 + 12) = 2
θ = tan-1 (1/√3)
As x > 0 and y > 0, Z lies in 1st quadrant and the value of θ is 0 ≤ θ ≤ π/2.
So, θ = π/6 and Z = 2 (cos (π/6) + i sin (π/6))
Therefore, the polar form of (√3 + i) is √2 (cos (π/6) + i sin (π/6)).
(iii) 1 – i
Solution:
We are given, Z = 1 – i, so x = 1 and y = –1.
|Z| = √(1)2 + (–1)2) = √2
θ = tan-1 (1/1) = tan-1 1
As x > 0 and y < 0, Z lies in 4th quadrant and the value of θ is –π/2 ≤ θ ≤ 0.
So, θ = – π/4 and,
Z = √2 (cos (–π/4) + i sin (–π/4))
= √2 (cos (π/4) – i sin (π/4))
Therefore, the polar form of (1 – i) is √2 (cos (π/4) – i sin (π/4)).
(iv) (1 – i)/(1 + i)
Solution:
We are given, Z = (1 – i)/(1 + i).
Multiplying and dividing by (1 – i), we get,
Z = 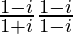
= 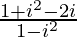
= 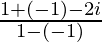
= 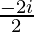
= 0 – i
So x = 0, y = –1 and |Z| = √(02 + (–1)2) = 1
θ = tan-1 (1/0)
As x ≥ 0 and y < 0, Z lies in 4th quadrant and the value of θ is –π/2 ≤ θ ≤ 0.
So, θ = –π/2 and,
Z = 1 (cos (–π/2) + i sin (–π/2))
= cos (π/2) – i sin (π/2)
Therefore, the polar form of (1 – i)/(1 + i) is cos (π/2) – i sin (π/2).
(v) 1/(1 + i)
Solution:
We are given, Z = (1 – i)/(1 + i).
Multiplying and dividing by (1 – i), we get,
Z = 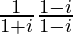
= 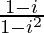
= 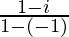
= 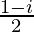
= 1/2 – i/2
So x = 1/2, y = –1/2 and |Z| = √((1/2)2 + (–1/2)2) = √(2/4) = 1/√2
θ = tan-1 ((1/2)/(1/2)) = tan–1 1
As x > 0 and y < 0, Z lies in 4th quadrant and the value of θ is –π/2 ≤ θ ≤ 0.
So, θ = –π/4 and,
Z = 1/√2 (cos (-π/4) + i sin (-π/4))
= 1/√2 (cos (π/4) – i sin (π/4))
Therefore, the polar form of 1/(1 + i) is 1/√2 (cos (π/4) – i sin (π/4)).
(vi) (1 + 2i)/(1 – 3i)
Solution:
We are given, Z = (1 + 2i)/(1 – 3i).
Multiplying and dividing by (1 + 3i), we get,
Z = 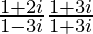
= 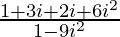
= 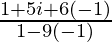
= 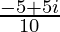
= –1/2 + i/2
So x = –1/2, y = 1/2 and |Z| = √((–1/2)2 + (1/2)2) = √(2/4) = 1/√2
θ = tan-1 ((1/2)/(1/2)) = tan–1 1
As x < 0 and y > 0, Z lies in 2nd quadrant and the value of θ is π/2 ≤ θ ≤ π.
So, θ = 3π/4 and Z = 1/√2 (cos (3π/4) + i sin (3π/4))
Therefore, the polar form of (1 + 2i)/(1 – 3i) is 1/√2 (cos (3π/4) + i sin (3π/4)).
(vii) sin 120o – i cos 120o
Solution:
We are given, Z = sin 120o – i cos 120o
= √3/2 – i (–1/2)
= √3/2 + i (1/2)
So x = √3/2, y = 1/2 and |Z| = √((√3/2)2 + (1/2)2) = √(3/4 + 1/4) = 1
θ = tan-1 ((1/2)/(√3/2)) = tan-1 (1/√3)
As x > 0 and y > 0, Z lies in 1st quadrant and the value of θ is 0 ≤ θ ≤ π/2.
So, θ = π/6 and Z = 1 (cos (π/6) + i sin (π/6))
Therefore, the polar form of √3/2 + i (1/2) is 1 (cos (π/6) + i sin (π/6)).
(viii) -16/(1 + i√3)
We are given, Z = –16/(1 + i√3).
Multiplying and dividing by (1 – i√3), we get,
Z = 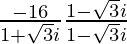
= 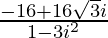
= 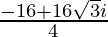
= –4 + 4√3 i
So x = –4, y = 4/√3 and |Z| = √((–4)2 + (4√3)2) = √(16 + 48) = 8
θ = tan-1 (4√3/4) = tan-1 (√3)
As x < 0 and y > 0, Z lies in 2nd quadrant and the value of θ is π/2 ≤ θ ≤ π.
So, θ = 2π/3 and Z = 8 (cos (2π/3) + i sin (2π/3))
Therefore, the polar form of -16 / (1 + i√3) is 8 (cos (2π/3) + i sin (2π/3)).
Question 2. Write (i25)3 in polar form.
Solution:
We are given,
Z = (i25)3
= i75
= (i2)37. i
= (–1)37. i
= – i
= 0 – i
So x = 0, y = –1 and,
|Z| = √(x2 + y2)
= √(02 + (–1)2)
= 1
θ = tan–1 (|y| / |x|)
= tan–1 (1 / 0)
Since x ≥ 0 and y < 0, Z lies in 4th quadrant and the value of θ is π/2 ≤ θ ≤ 0. So, θ = –π/2.
Z = 1 (cos (–π/2) + i sin (–π/2))
= 1 (cos (π/2) – i sin (π/2))
Therefore, the polar form of (i25)3 is 1 (cos (π/2) – i sin (π/2)).
Question 3. Express the following complex numbers in the form r (cos θ + i sin θ):
(i) 1 + i tan α
(ii) tan α – i
(iii) 1 − sin α + i cos α
(iv) 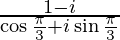
Solution:
(i) 1 + i tan α
We are given 1 + i tan α, so x =1 and y = tan α.
We also know that tan α is a periodic function with period π.
So α is lying in the interval [0, π/2) ∪ (π/2, π].
Case 1: If α ∈ [0, π/2)
|Z| = r = √(12 + tan2 α)
= √( sec2 α)
= sec α
θ = tan-1 (tan α/1)
= tan-1 (tan α)
= α
So, Z = sec α (cos α + i sin α)
Therefore, polar form is sec α (cos α + i sin α).
Case 2: α ∈ (π/2, π]
|Z| = r = √(12 + tan2 α)
= √( sec2 α)
= – sec α
θ = tan-1 (tan α/1)
= tan-1 (tan α)
= –π + α
So, Z = –sec α (cos (α – π) + i sin (α – π))
Therefore, polar form is –sec α (cos (α – π) + i sin (α – π)).
(ii) tan α – i
We are given tan α – i, so x =tan α and y = –1.
We also know that tan α is a periodic function with period π.
So α is lying in the interval [0, π/2) ∪ (π/2, π].
Case 1: If α ∈ [0, π/2)
|Z| = r = √(tan2 α + 1)
= √( sec2 α)
= sec α
θ = tan-1 (1/tan α)
= tan-1 (cot α)
= α – π/2
So, Z = sec α (cos (α – π/2) + i sin (α – π/2))
Therefore, polar form is sec α (cos (α – π/2) + i sin (α – π/2)).
Case 2: α ∈ (π/2, π]
|Z| = r = √(tan2 α + 1)
= √( sec2 α)
= – sec α
θ = tan-1 (1/tan α)
= tan-1 (cot α)
= π/2 + α
So, Z = –sec α (cos (π/2 + α) + i sin (π/2 + α))
Therefore, polar form is –sec α (cos (π/2 + α) + i sin (π/2 + α)).
(iii) 1 − sin α + i cos α
Let z = 1 − sin α + i cos α
As sine and cosine functions are periodic functions with period 2π, let us take α in [0, 2π].
Now, z = 1 − sin α + i cos α
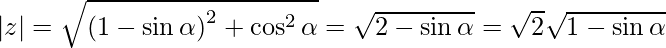
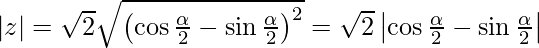
Let θ be an acute angle given by,
tan θ = 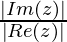
tan θ = 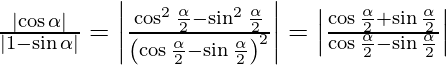
tan θ = 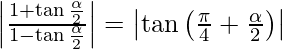
Case 1: When 0 ≤ α < π/2
In this case, we have,
|z| = √2(cos α/2 – sin α/2)
Also,
tan θ = |tan (π/4 + α/2)| = tan (π/4 + α/2)
θ = π/4 + α/2
Clearly, z lies in the first quadrant . Therefore, arg(z) = π/4 + α/2
Therefore, the polar form of z is √2(cos α/2 – sin α/2){cos (π/4 + α/2) + i sin (π/4 + α/2)}.
Case 2: When π/2 < α < 3π/2
In this case, we have,
|z| = |√2(cos α/2 – sin α/2)| = -√2(cos α/2 – sin α/2)
And, tan θ = |tan (π/4 + α/2)| = -tan (π/4 + α/2) = tan {π – (π/4 + α/2)} = tan (α/2 – 3π/4)
θ = 3π/4 + α/2
Clearly, z lies in the fourth quadrant . Therefore, arg(z) = -θ = 3π/4 + α/2 = α/2 – 3π/4
Therefore, the polar form of z is -√2(cos α/2 – sin α/2){cos (α/2 – sin 3π/4) + i sin (α/2 – sin 3π/4)}..
Case 3: When 3π/2 < α < 2π
In this case, we have,
|z| = |√2(cos α/2 – sin α/2)| = -√2(cos α/2 – sin α/2)
And tan θ = |tan (π/4 + α/2)| = tan (π/4 + α/2) = – tan {π – (π/4 + α/2)} = tan (α/2 – 3π/4)
θ = α/2 – 3π/4
Clearly, z lies in the first quadrant . Therefore, arg(z) = θ = α/2 – 3π/4
Therefore, the polar form of z is -√2(cos α/2 – sin α/2){cos (α/2 – sin 3π/4) + i sin (α/2 – sin 3π/4)}.
(iv) 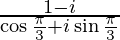
Let z = 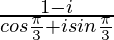
= 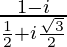
= 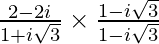
= 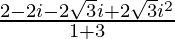
= 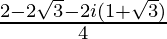
= 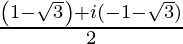
= 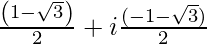
Now, z = 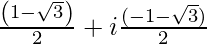
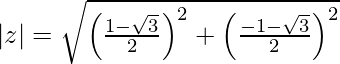
= 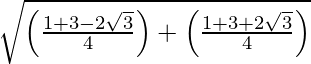
= 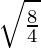
= √2
Let θ be an acute angle given by tan θ = 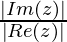
tan θ = 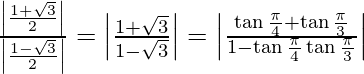
tan θ = |tan (π/4 + π/3)| = |tan 7π/12|
θ = 7π/12
Clearly, z lies in the fourth quadrant . Therefore, arg(z) = -7π/12
Therefore, the polar form of z is √2(cos 7π/12 – sin 7π/12).
Question 4. If z1 and z2 are two complex number such that |z1| = |z2| and arg (z1) + arg (z2) = π, then show that 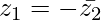 .
.
Solution:
We are given |z1| = |z2| and arg (z1) + arg (z2) = π. Suppose arg (z1) = θ, then arg (z2) = π – θ.
We know z = |z| (cos θ + i sin θ)
z2 = |z2| (cos (π – θ) + i sin (π – θ))
= |z2| (–cos θ + i sin θ)
= – |z2| (cos θ – i sin θ)
The conjugate of z2, 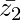 = – |z2| (cos θ + i sin θ)
= – |z2| (cos θ + i sin θ)
Now L.H.S. = z1 = |z1| (cos θ + i sin θ)
= |z2| (cos θ + i sin θ)
= – [– |z2| (cos θ + i sin θ)]
= 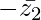
= R.H.S.
Hence proved.
Question 5. If z1, z2 and z3, z4 are two pairs of conjugate complex numbers, prove that arg (z1/z4) + arg (z2/z3) = 0
Solution:
We are given,
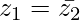
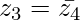
L.H.S. = arg (z1/z4) + arg (z2/z3)
= arg (z1) − arg (z4) + arg (z2) − arg (z3)
= [arg (z1) + arg (z2)] − [arg (z3) + arg (z4)]
= ![Rendered by QuickLaTeX.com [arg(z_2)+arg(\bar{z_2})]−[arg(z_4)+arg(\bar{z_4})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-129f0da71b166cf09a7519e4fed48e01_l3.png)
= 0 − 0
= 0
= R.H.S
Hence proved.
Question 6. Express sin π/5 + i (1 – cos π/5) in polar form.
Solution:
We are given,
Z = sin π/5 + i (1 – cos π/5)
= 2 sin π/10 cos π/10 + i (2 sin2 π/10)
= 2 sin π/10 (cos π/10 + i sin π/10)
We know the polar form is given by r (cos θ + i sin θ).
Therefore, the polar form of the given expression is 2 sin π/10 (cos π/10 + i sin π/10).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...