Class 11 RD Sharma Solutions – Chapter 13 Complex Numbers – Exercise 13.2 | Set 1
Last Updated :
30 Apr, 2021
Question 1. Express the following complex numbers in the standard form a + ib:
(i) (1 + i) (1 + 2i)
Solution:
We have, z = (1 + i) (1 + 2i)
= 1 (1 + 2i) + i (1 + 2i)
= 1 + 2i + i + 2i2
= 1 + 3i + 2(−1)
= 1 + 3i − 2
= −1 + 3i
Therefore, the standard form is −1 + 3i where a = −1 and b = 3.
(ii) 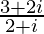
Solution:
We have, z =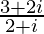
=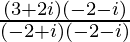
=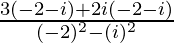
=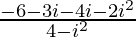
=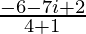
=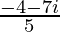
Therefore, the standard form is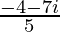 where a = −4/5 and b = −7/5.
where a = −4/5 and b = −7/5.
(iii)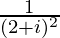
Solution:
We have, z =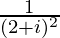
=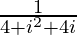
=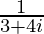
=
=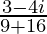
=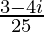
Therefore, the standard form is where a = 3/25 and b = −4/25.
where a = 3/25 and b = −4/25.
(iv)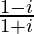
Solution:
We have, z =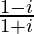
=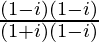
=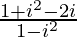
=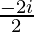
= −i
Therefore, the standard form is −i where a = 0 and b = −1.
(v)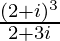
Solution:
We have, z =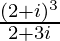
=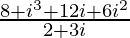
=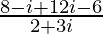
=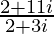
=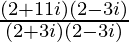
=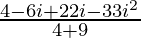
=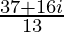
Therefore, the standard form is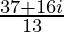 where a = 37/13 and b = 16/13.
where a = 37/13 and b = 16/13.
(vi)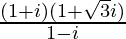
Solution:
We have, z =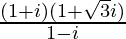
=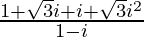
=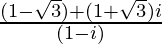
=}{(1-i)(1+i)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f1c1a8f66a739449b23d64b1caae565_l3.png)
=![Rendered by QuickLaTeX.com \frac{[1-\sqrt{3}+(1-\sqrt{3})i+(1+\sqrt{3})i+(1+\sqrt{3})i^2]}{(1-(-1))}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-738b20ec0962d762d74a3e08dd2ca288_l3.png)
=![Rendered by QuickLaTeX.com \frac{[(1-\sqrt{3})+(1-\sqrt{3}+1+\sqrt{3})i+(1+\sqrt{3})(-1)]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-12d45747c419c6402c51c443ea250a37_l3.png)
=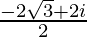
= –√3 + i
Therefore, the standard form is –√3 + i where a = –√3 and b = 1.
(vii)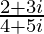
Solution:
We have, z =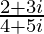
=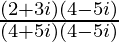
=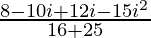
=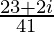
Therefore, the standard form is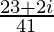 where a = 23/41 and b = 2/41.
where a = 23/41 and b = 2/41.
(viii)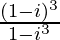
Solution:
We have, z =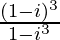
=
=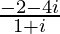
=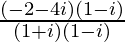
=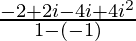
=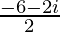
= –3 – i
Therefore, the standard form is –3 – i where a = –3 and b = – 1.
(ix) (1 + 2i)-3
Solution:
We have z = (1 + 2i)-3
=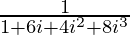
=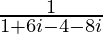
=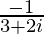
=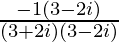
=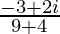
=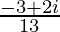
Therefore, the standard form is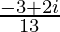 where a = –3/13 and b = 2/13.
where a = –3/13 and b = 2/13.
(x)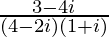
Solution:
We have, z =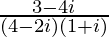
=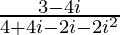
=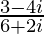
=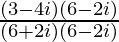
=
=
=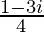
Therefore, the standard form is where a = –1/4 and b = –3/4.
where a = –1/4 and b = –3/4.
(xi)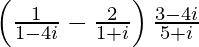
Solution:
We have, z =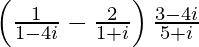
=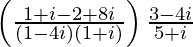
=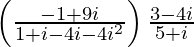
=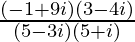
=
=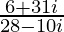
=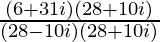
=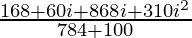
=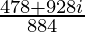
Therefore, the standard form is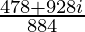 where a = 478/884 and b = 928/884.
where a = 478/884 and b = 928/884.
(xii)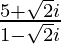
Solution:
We have, z =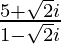
=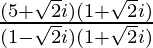
=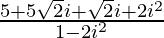
=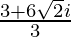
= 1+ 2√2i
Therefore, the standard form is 1+ 2√2i where a = 1 and b = 2√2.
Question 2. Find the real values of x and y, if
(i) (x + iy) (2 – 3i) = 4 + i
Solution:
We have,
=> (x + iy) (2 – 3i) = 4 + i
=> 2x – 3xi + 2yi – 3yi2 = 4 + i
=> 2x + (–3x+2y)i + 3y = 4 + i
=> (2x+3y) + i(–3x+2y) = 4 + i
On comparing real and imaginary parts on both sides, we get,
2x + 3y = 4 . . . . (1)
And –3x + 2y = 1 . . . . (2)
On multiplying (1) by 3 and (2) by 2 and adding, we get
=> 6x – 6x – 9y + 4y = 12 + 2
=> 13y = 14
=> y = 14/13
On putting y = 14/13 in (1), we get
=> 2x + 3(14/13) = 4
=> 2x = 4 – (42/13)
=> 2x = 10/13
=> x = 5/13
Therefore, the real values of x and y are 5/13 and 14/13 respectively.
(ii) (3x – 2iy) (2 + i)2 = 10(1 + i)
Solution:
We have,
=> (3x – 2iy) (2 + i)2 = 10(1 + i)
=> (3x – 2yi) (4 + i2 + 4i) = 10 + 10i
=> (3x – 2yi) (3 + 4i) = 10+10i
=> 3x – 2yi =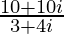
=> 3x – 2yi =
=> 3x – 2yi =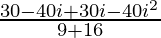
=> 3x – 2yi =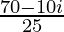
On comparing real and imaginary parts on both sides, we get,
=> 3x = 70/25 and –2y = –10/25
=> x = 70/75 and y = 1/5
Therefore, the real values of x and y are 70/75 and 1/5 respectively.
(iii)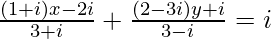
Solution:
We have,
=>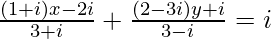
=>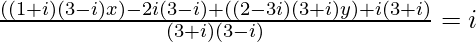
=>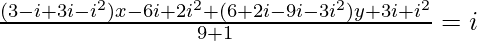
=> (4+2i) x − 3i − 3 + (9−7i)y = 10i
=> (4x+9y−3) + i(2x−7y−3) = 10i
On comparing real and imaginary parts on both sides, we get,
4x + 9y − 3 = 0 . . . . (1)
And 2x − 7y − 3 = 10 . . . . (2)
On multiplying (1) by 7 and (2) by 9 and adding, we get,
=> 28x + 18x + 63y – 63y = 117 + 21
=> 46x = 117 + 21
=> 46x = 138
=> x = 3
On putting x = 3 in (1), we get
=> 4x + 9y − 3 = 0
=> 9y = −9
=> y = −1
Therefore, the real values of x and y are 3 and −1 respectively.
(iv) (1 + i) (x + iy) = 2 – 5i
Solution:
We have,
=> (1 + i) (x + iy) = 2 – 5i
=> x + iy =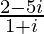
=> x + iy =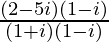
=> x + iy =
=> x + iy =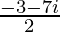
On comparing real and imaginary parts on both sides, we get,
=> x = −3/2 and y = −7/2
Therefore, the real values of x and y are −3/2 and −7/2 respectively.
Question 3. Find the conjugates of the following complex numbers:
(i) 4 – 5i
Solution:
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of (4 – 5i) is (4 + 5i).
(ii)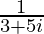
Solution:
We have, z =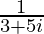
=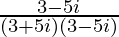
=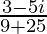
=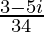
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of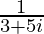 is
is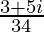 .
.
(iii)
Solution:
We have, z =
=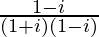
=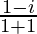
=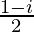
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of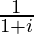 is
is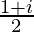 .
.
(iv)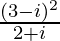
Solution:
We have, z =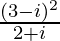
=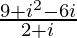
=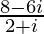
=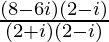
=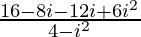
=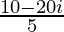
= 2 – 4i
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of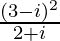 is 2 + 4i.
is 2 + 4i.
(v)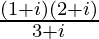
Solution:
We have, z =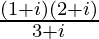
=
=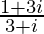
=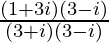
=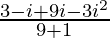
=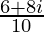
=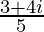
We know the conjugate of a complex number (a + ib) is (a – ib).
The conjugate of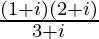 is
is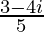 .
.
(vi)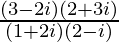
Solution:
We have, z =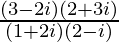
=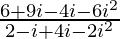
=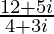
=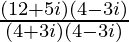
=
=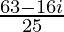
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of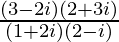 is
is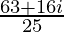 .
.
Question 4. Find the multiplicative inverse of the following complex numbers:
(i) 1 – i
Solution:
We have z = 1 – i
We know the multiplicative inverse of a complex number z is 1/z. So, we get,
=
=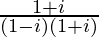
=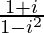
=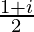
Therefore, the multiplicative inverse of (1 – i) is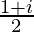 .
.
(ii) (1 + i √3)2
Solution:
We have, z = (1 + i √3)2
= 1 + 3i2 + 2 i√3
= 1 + 3(−1) + 2 i√3
= 1 – 3 + 2 i√3
= −2 + 2 i√3
We know the multiplicative inverse of a complex number z is 1/z. So, we get,
=
=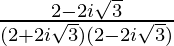
=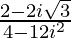
=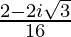
=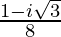
Therefore, the multiplicative inverse of (1 + i √3)2 is .
.
(iii) 4 – 3i
Solution:
We have z = 4 – 3i
We know the multiplicative inverse of a complex number z is 1/z. So, we get,
=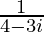
=
=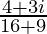
=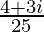
Therefore, the multiplicative inverse of 4 – 3i is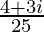 .
.
(iv) √5 + 3i
Solution:
We have z = √5 + 3i
We know the multiplicative inverse of a complex number z is 1/z. So, we get,
=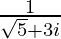
=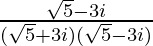
=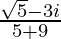
=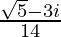
Therefore, the multiplicative inverse of √5 + 3i is .
.
Question 5. If z1 = 2 − i, z2 = 1 + i, find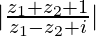 .
.
Solution:
Given z1 = 2 − i, z2 = 1 + i, we get,
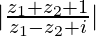 =
=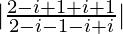
=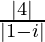
=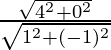
=
= 2√2
Therefore, the value of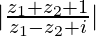 is 2√2.
is 2√2.
Question 6. If z1 = (2 – i), z2 = (–2 + i), find
(i) Re
Solution:
Given z1 = (2 – i), z2 = (–2 + i), we get,
 =
=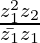
=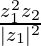
=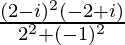
=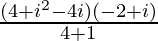
=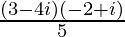
=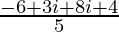
=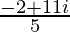
Therefore, Re =
=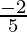 .
.
(ii) Im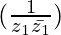
Now,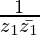 =
=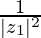
=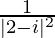
=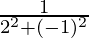
=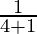
=
Therefore, Im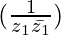 = 0.
= 0.
Question 7. Find the modulus of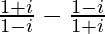 .
.
Solution:
We have, z =
=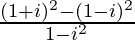
=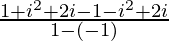
=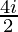
= 2i
So, modulus of z =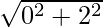 = 2.
= 2.
Therefore, the modulus of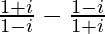 is 2.
is 2.
Question 8. If x + iy =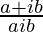 , prove that x2 + y2 = 1.
, prove that x2 + y2 = 1.
Solution:
We have,
=> x + iy =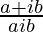
On applying modulus on both sides we get,
=> |x + iy| =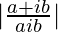
=> |x + iy| =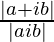
=>
=>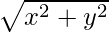 = 1
= 1
=> x2 + y2 = 1
Hence proved.
Question 9. Find the least positive integral value of n for which![Rendered by QuickLaTeX.com \left[\frac{1+i}{1-i}\right]^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8645087921c320291ee1c71ccf3d648_l3.png) is real.
is real.
Solution:
We have, z =![Rendered by QuickLaTeX.com \left[\frac{1+i}{1-i}\right]^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3b45f08174505421a700468532578b4_l3.png)
=![Rendered by QuickLaTeX.com \left[\frac{(1+i)^2}{(1-i)(1+i)}\right]^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fb6401a263bfd80d22eda10d40481573_l3.png)
=![Rendered by QuickLaTeX.com \left[\frac{1+i^2+2i}{1-i^2}\right]^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6729e94f507c993ee7118323891d091e_l3.png)
=![Rendered by QuickLaTeX.com \left[\frac{2i}{2}\right]^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-08ea063446da2cdb8cfe9aba5318e390_l3.png)
= in
For n = 2, we have in = i2 = −1, which is real
Therefore, the least positive integral value of n for which![Rendered by QuickLaTeX.com \left[\frac{1+i}{1-i}\right]^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8645087921c320291ee1c71ccf3d648_l3.png) is real is 2.
is real is 2.
Question 10. Find the real values of θ for which the complex number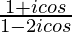 is purely real.
is purely real.
Solution:
We have, z =
=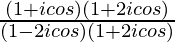
=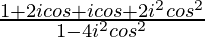
=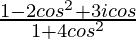
=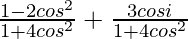
For a complex number to be purely real, the imaginary part should be equal to zero.
So, we get,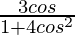 = 0
= 0
=> cos θ = 0
=> cos θ = cos π/2
=> 2nπ ± π/2, for n ∈ Z
Therefore, the values of θ for the complex number to be purely real are 2nπ ± π/2, for n ∈ Z.
Question 11. Find the smallest positive integer value of n for which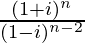 is a real number.
is a real number.
Solution:
We have, z =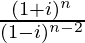
=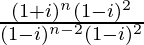
=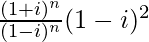
=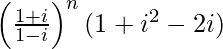
=![Rendered by QuickLaTeX.com \left[\frac{(1+i)^2}{(1-i)(1+i)}\right]^n×(-2i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-779d19f235320eb0c7a4e5235585b7ba_l3.png)
=![Rendered by QuickLaTeX.com \left[\frac{1+i^2+2i}{1-i^2}\right]^n×(-2i)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-12063da2412ddd59a1bf4d2305391591_l3.png)
=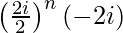
= in × (−2i)
= −2in+1
For n = 1, we have z = −2i1+1
= −2i2
= 2, which is real
Therefore, the smallest positive integer value of n for which is a real number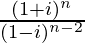 is 1.
is 1.
Question 12. If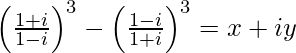 , find (x, y).
, find (x, y).
Solution:
We have,
=>![Rendered by QuickLaTeX.com \left[\frac{(1+i)^2}{(1-i)(1+i)}\right]^3-\left[\frac{(1-i)^2}{(1+i)(1-i)}\right]^3=x+iy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9602a571223758c3c80bc9c8507ad7b2_l3.png)
=>![Rendered by QuickLaTeX.com \left[\frac{1+i^2+2i}{1-i^2}\right]^3-\left[\frac{1+i^2-2i}{1-i^2}\right]^3=x+iy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d988d3c1ecd473deacf0be32db917a9_l3.png)
=>![Rendered by QuickLaTeX.com \left[\frac{2i}{2}\right]^3-\left[\frac{-2i}{2}\right]^3=x+iy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5e2e76084144601995b0db83c6b9bfd4_l3.png)
=> i3 – (–i3) = x + iy
=> 2i3 = x + iy
=> x + iy = −2i
On comparing real and imaginary parts on both sides, we get,
=> (x, y) = (0, −2)
Question 13. If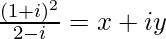 , find x + y.
, find x + y.
Solution:
We have,
=>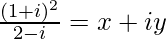
=>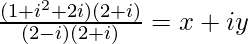
=>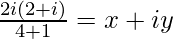
=>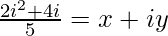
=>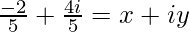
On comparing real and imaginary parts on both sides, we get,
=> x = −2/5 and y = 4/5
So, x + y = −2/5 + 4/5
= (−2+4)/5
= 2/5
Therefore, the value of (x + y) is 2/5.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...