Class 11 RD Sharma Solutions – Chapter 1 Sets – Exercise 1.6 | Set 2
Last Updated :
11 Feb, 2021
Question 8. Find sets A, B and C, such that A ∩ B and B ∩ C and A ∩ C are non-empty sets, and A ∩ B ∩ C = ϕ
Solution:
Let us consider the sets,
A = {5, 6, 10}
B = {6, 8, 9}
C = {9, 10, 11}
Now, we have,
A ∩ B = 6 ≠ ϕ
B ∩ C = 9 ≠ ϕ
A ∩ C = 10 ≠ ϕ
And, A ∩ B ∩ C = ϕ
Now, we have A ∩ B and B ∩ C and A ∩ C as non-empty sets, but A ∩ B ∩ C is empty set.
Question 9. For any two sets A and B, prove that A ∩ B = ϕ => A ⊂ B’
Solution:
Let, a ∈ A => a ∉ B
Thus,
A ∩ B = ϕ
=> a ∈ B’
Thus, a ∈ A and a ∈ B’ => A ⊂ B’
Question 10. Prove the following:
(i) A – B and A ∩ B are disjoint sets
(ii) B – A and A ∩ B are disjoint sets
(iii) A – B and B – A are disjoint sets
Solution:
(i) A – B and A ∩ B
Let a ∈ A – B => a ∈ A and a ∉ B => a ∉ A ∩ B
Therefore, A – B and A ∩ B are disjoint sets.
(ii) Let a ∈ B – A => a ∈ B and a ∉ A => a ∉ A ∩ B
Hence, B – A and A ∩ B are disjoint sets.
(iii) A – B and B – A,
A – B = x, x : x ∈ A and x ∉ B
A – B and B – A are disjoint sets.
Question 11. Using properties of sets, show that for any two sets A and B,
(A ∪ B) ∩ (A ∩ B’) = A
Solution:
We have,
LHS = A ∪ B ∩ A ∩ B’
Solving this, we get,
= A ∪ B ∩ A ∪ A ∪ B ∩ B’
= A ∪ A ∪ B ∩ B’
Since, B ∩ B’ = ∅
= A ∪ A ∩ B’
= A
Therefore, LHS = RHS.
Question 12.
(i)Show that for any two sets A and B,
A’ U B = U => A ⊂ B
(ii) Show that for any two sets A and B,
B’ ⊂ A’ = U => A ⊂ B
Solution:
(i) Let a ∈ A
= a ∈ U
= a ∈ A’ ∪ B, because, U = A’ ∪ B
= a ∈ B, because a ∉ A’
Hence, A ⊂ B
(ii) Let a ∈ A
= a ∉ A’
= a ∉ B’, because, B’ is a subset of A’
= a ∈ B
Hence, A ⊂ B
Question 13. Is it true that for any set A and B, P(A) ∪ P(B) = P(A ∪ B)? Justify your answer.
Solution:
Result is False.
Proof:
Let X ∈ P(A) ∪ P(B)
= X ∈ P(A) or X ∈ P(B)
= X ⊂ A or X ⊂ B
= X ⊂ A U B
= X ∈ P(A ∩ B)
Thus, P(A) ∪ P(B) ⊂ P(A ∪ B)
Also, Let us assume,
X ∈ P(A ∪ B). But, X ∉ P(A) or X ∉ P(B)
For instance, we have X = 1, 2, 3, 4 and A = 2, 5 and B = 1, 3, 4.
So, X ∉ P(A) ∪ P(B)
Therefore, P(A ∪ B) doesn’t necessarily have to be a subset of P(A) ∪ P(B).
Question 14.
(i) Show that For any sets A and B,
A = (A ∩ B) ∩ (A – B)
(ii) Show that For any sets A and B,
A ∪ (B – A) = A ∪ B
Solution:
(i) We have,
RHS = (A ∩ B) ∪ (A – B)
= (A ∩ B) ∪ (A ∩ B)’
= (A ∩ B) ∪ (A ∩ A) ∩ (B ∪ B)’
= A ∩ (A ∪ B)’ ∩ (B ∪ B)’
= A ∩ (A ∪ B)’ ∩ U
= A ∩ (A ∪ B)’
= A
Therefore, RHS = LHS
(ii) We have,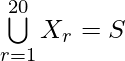
LHS = A ∪ (B – A)
= A ∪ (B ∩ A)’
= (A ∪ B) ∩ (A ∪ A)’
= (A ∪ B) ∩ U
LHS = A ∪ B = RHS
Question 15. Each set X, contains 5 elements and each set Y, contains 2 elements and 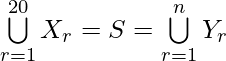 each element of S belongs to exactly 10 of the Xr’s and to exactly 4 of Yr’s, then find the value of n.
each element of S belongs to exactly 10 of the Xr’s and to exactly 4 of Yr’s, then find the value of n.
Solution:
We have, Each set X contains 5 elements, and 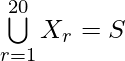
Therefore, n(S) = 20 x 5 = 100
But, we know, that each of the element of S belong to exactly 10 of the Xr‘s.
Therefore, n(S) = 100/10 = 10 -(1)
Also, Y contains 2 elements and
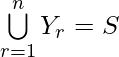
Therefore, n(S) = n x 2 = 2n
Each of the element of S belong to exactly 4 of the Yr’s.
n(S) = 2n/4 = n/2 -(2)
From equation (1) and (2)
10 = n/2
n = 20
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...