Class 11 RD Sharma Solutions – Chapter 1 Sets – Exercise 1.4 | Set 2

Question 9. Write down all subsets of the following subsets: 

(i) {a}

(ii) {0,1}

(iii){a,b,c}

(iv){1,{1}}

(v) {ϕ}

Solution:

We know, if A is a set and B is a subset of A, then B is a subset of A, then B is called a proper subset of A if B ⊆ A and B≠A, ϕ, illustrated by B ⊆ A or B ⊂ A. 

For any set S with n elements, the power set has 2ⁿ elements. 

(i) Since n=1, the power set has 2¹ = 2 elements.The subsets are {a} and ϕ, but the set has no proper subsets. 

(ii) Since n=2, the power set has 2² = 4 elements. The elements of the power subset are ϕ, {0}, {1}, {0,1}.

(iii)Since n=3, the power set has 2³ = 8 elements.The elements of the power subset are ϕ, {a}, {b}, {c}, {a,b}, {b,c}, {a,c}, {a,b,c}.

(iv) Since n=2, the power set has 2² = 4 elements. The elements of the power subset are ϕ, {1}, {{1}}, {1,{1}}.

(v)Since n=1, the power set has 2¹ = 2 elements, which are ϕ and {ϕ}.

Question 10. Write down all proper subsets of the following subsets: 

(i) {1,2}

(ii) {1,2,3}

(iii){1}

Solution: 

We know, if A is a set and B is a subset of A, then B is a subset of A, then B is called a proper subset of A if B ⊆ A and B≠A, ϕ, illustrated by B ⊆ A or B ⊂ A.

(i) The proper subsets are {1}, {2}

(ii) The proper subsets are {1}, {2}, {3}, {1,3}, {2,3}, {1,2}

(iii) The subsets are {1} and ϕ, but the set has no proper subsets. 

Question 11. What is the total number of proper subsets of a set consisting of n elements?

Solution

We know that, for any finite set A, having n elements, the total number of subsets of A has 2ⁿ elements. However, the number of proper subsets is 2ⁿ – 1, where A is not included. 

Question 12. If A is any set, prove that A ⊆ ∅ <=> A = ∅

Solution:

In order to prove that two sets A and B are equal, we need to show the following:

A ⊆ B and B ⊆ A.

Since, ∅ is a subset of every set, therefore, A ⊆ ∅.

Therefore, ∅ ⊆ A.

Hence, A = ∅

Let us assume now, that A =∅

Now, every set is a subset of itself, 

∅ = A ⊆ ∅ 

Hence, proved.  

Question 13. Prove that A ⊆ B, B ⊆ C, and C ⊆ A => A = C

Solution:

We have, A ⊆ B, B ⊆ C and C ⊆ A, therefore, A ⊆ B ⊆ C ⊆ A. 

Now, A is a subset of B and B is a subset of C,

So A is a subset of C, that is A ⊆ C.

Also, it is given, C ⊆ A.

We know, if A ⊆ C and C ⊆ A => A = C. 

Hence, proved. 

Question 14. How many elements has P(A)=?, if A = ∅.

Solution:

An empty set has zero elements. 

Therefore, size of A = n = 0. 

Power set of A P(A) = 2ⁿ = 2⁰ = 1 element. 

Question 15. What universal set(s) would you propose for the following? 

(i) The set of right triangles.

(ii) The set of isosceles triangles. 

Solution:

(i) The right triangle is a subset of the triangles. Therefore, the set of right triangles is a subset of set of triangles. 

=> Set of right triangles ⊆ Set of triangles, which becomes Universal set (U) in this case. 

(ii) The isosceles triangle is a special case of the triangles where two sides are equal. Therefore, the set of isosceles triangles is a subset of set of triangles.

=> Set of isosceles triangles ⊆ Set of triangles, which becomes Universal set (U) in this case. 

Question 16. If X= {8ⁿ – 7n -1 : n ∈ N} and Y = {49(n-1): n ∈ N}. Prove that X ⊆ Y.

Solution:

To prove X ⊆ Y, we need to show that each element of X belongs to Y. 

We have, 

X= {8ⁿ – 7n -1 : n ∈ N} 

Y = {49(n-1): n ∈ N}

So, let x ∈ X => x = 8^m– 7m – 1  for some m ∈ N

=> x = (1 + 7 )^m – 7m – 1

= {n \choose x}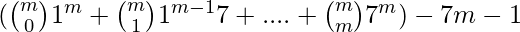

= 

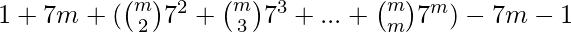
=({m \choose 0}1^m + {m \choose 1}1^{m-1} 7 +….+ {m \choose m}7^{m}) – 7m -1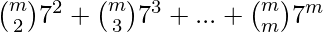 

=49({m \choose 2}7^2 + {m \choose 3}7^{3} +…+ {m \choose m}7^{m-2}), m >=2 

= 49t_m, m >=2 where t_m = {m \choose 2}7^2 + {m \choose 3}7^{3} +…+ {m \choose m}7^{m-2}

For m = 1, we have, 

X = 8 – 7 x 1 – 1

   = 0

Hence, X contains all positive integral multiples of 49. 

Hence, Y contains all positive integral multiples of 49 and 0, for n =1.

Therefore, 

 X ⊆ Y.

My Personal Notes arrow_drop_up

Save