Question 17. If the 4th, 10th and 16th terms of a G.P. are x, y, and z, respectively. Prove that x, y, z are in G.P.
Solution:
Let the first term of G.P. be a and common ratio be r.
According to the question
a4 = ar3 = x ……(1)
a10 = ar9 = y ……(2)
a16 = ar15 = z ……(3)
Now divide eq(2) by (1), we get
ar9/ar3 = y /x
r6 = y /x
Divide eq(3) by (2), we get
ar15/ar9 = z/y
r6 = z/y
y /x = z/y
So x, y, z are in G.P.
Question 18. Find the sum to n terms of the sequence, 8, 88, 888, 8888…
Solution:
According to the question
Given Sequence: 8, 88, 888, 8888…
This sequence is neither A.P. nor G.P. but we can change it into G.P.
So, we can write as:
Sn = 8 + 88 + 888 + 8888 + … + n times
= 8(1 + 11 + 111 + 1111 + … + n times)
= 8/9(9 + 99 + 999 + 9999 + … + n times)
= 8/9((10 – 1) + (102 – 1) + (103 – 1) + (104 – 1) + … + n times)
= 8/9((10 + 102 + 103 + 104 + … + n times) – (1 + 1 + 1 + 1 + ….+ n terms))
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
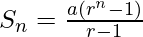
=![Rendered by QuickLaTeX.com \frac{8}{9}[\frac{10(10^n - 1)}{10 - 1}-n]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-59312a37391bc70b3d0baf0da0ec710c_l3.png)
= ![Rendered by QuickLaTeX.com \frac{8}{9}[\frac{(10^{n+1} - 10)}{9}-n]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7ecf14d7cfea4697144be32b43112329_l3.png)
Question 19. Find the sum of the products of the corresponding terms of the sequences 2, 4, 8,16, 32 and 128, 32, 8, 2, 1/2.
Solution:
According to the question
Sequence 1: 2, 4, 8, 16, 32
Sequence 2: 128, 32, 8, 2, 1/2
Product of corresponding terms are
= 2 x 128, 4 x 32, 8 x 8, 16 x 2, 32 x 1/2
= 256, 128, 64, 32, 16
So, the first term(a) = 256
Common ration = 1/2
S5 = 256[1 – (1/2)5]/1/2
= 496
Question 20. Show that the products of the corresponding terms of the sequences a, ar, ar2 , …arn – 1 and A, AR, AR2, … ARn – 1 form a G.P, and find the common ratio.
Solution:
According to the question
Sequence 1: a, ar, ar2 , …arn – 1
Sequence 2: A, AR, AR2, … ARn – 1
Prove: aA, arAR, ar2AR2, …. arn – 1ARn – 1 from G.P
Now we find the common ration of the G.P
r = arAR. aA = rR
Again,
r = ar2AR2/arAR = rR
Hence, the sequence form G.P. and the common ratio is rR
Question 21. Find four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the 4th by 18.
Solution:
Let us considered a be the first term, r be the common ratio and
four numbers in G.P. are a, ar, ar2,ar3
According to the question
So, a3 = a1 + 9
ar2 = ar + 9
ar2 – ar = 9 ….(1)
a2 = a4 + 18
ar = ar3 + 18
ar – ar3 = 18 ….(2)
Now divide eq(2) by (1), we get
ar – ar3/ar2 – ar = 18/9
ar (1 – r2)/-a(1 – r2) = 2
ar/-a = 2
r = -2
Now put the value of r in eq(1), we get the value of a
a(-2)2 – a(-2) = 9
a = 3
Hence, the four numbers in G.P. are 3, 3(-2), 3(-2)2,3(-2)3
= 3, -6, 12, -24.
Question 22. If the p th, qth, and rth terms of a G.P. are a, b and c, respectively. Prove that aq–rbr–pcp–q = 1.
Solution:
Let us considered the 1st term of a G.P. be k and common ratio x.
According to the question
kxp-1 = a ….(1)
kxq-1 = b ….(2)
kxr-1 = c ….(3)
Prove: aq–rbr–pcp–q = 1
Proof:
Lets take L.H.S
i.e., aq–rbr–pcp–q
Now put the value of a, b, c from the above equations,
aq – rbr – pcp – q = (kxp – 1)q – r(kxq – 1)r – p(kxr – 1)p – q
= k0 x x0
= 1
L.H.S = R.H.S
Question 23. If the first and the nth term of a G.P. are a and b, respectively, and if P is the product of n terms, prove that P2 = (ab)n.
Solution:
According to the question
The first term of the G.P. is a and the last term is b
Let the G.P. are a, ar, ar2,ar3. Here, r be the common ratio.
Then b = arn-1
Now, Product of n terms(P) = a x ar x ar2 x … x arn-1
P = anr{1 + 2 + …n – 1}
P = anr{(n(n – 1)/2}
So, P2 = a2nr(n(n – 1)
= [a2r(n – 1)]n
= [a x ar(n – 1)]n
= [ab]n
Hence Proved.
Question 24. Show that the ratio of the sum of first n terms of a G.P. to the sum of terms from (n + 1)th to (2n)th term is 1/rn.
Solution:
Let the first term of G.P. be a and the common ratio be r.
So, the sum of 1st n terms is 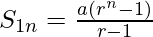
According to the question
Sum of (n+1)th to (2n)th term is 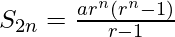
The required ratio is:
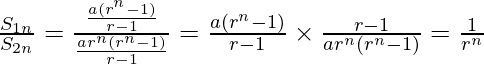
Question 25. If a, b, c and d are in G.P. show that (a2 + b2 + c2)(b2 + c2 + d2) = (ab + bc + cd)2
Solution:
According to the question
a, b, c, d are in G.P., so let the common ratio of G.P.be r.
Then b = ar, c = ar2, d = ar3
Simplifying LHS by putting value of b, c, d
(a2 + b2 + c2)(b2 + c2 + d2) = (a2 + a2r2 + a2r4)(a2r2 + a2r4 + a2r6)
= a4r2(1 + r2 + r4)2
Now, simplifying RHS
(ab + bc + cd)2 = (a2r + a2r3 + a2r5)2 = a4r2(1 + r2 + r4)2
LHS = RHS
Question 26. Insert two numbers between 3 and 81 so that the resulting sequence is G.P.
Solution:
Let us considered x1 and x2 be the two numbers in between 3 and 81. So, the G.P. is 3, x1, x2, 81 and
r be the common ratio. First term of the G.P.(a) = 3
So, a4 = 81
(3)r3 = 81
r3 = 27
r = 3
So, x1 = ar = 3 x 3 = 9
x2 = ar2 = (3)(3)2 = 27
Hence, the G.P. is 3, 9, 27, 81
Question 27. Find the value of n so that 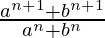 may be the geometric mean between a and b.
may be the geometric mean between a and b.
Solution:
G.M. between a and b is √ab
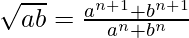
On squaring both side we get
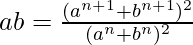
ab(an + bn)2 = (an + 1 + bn + 1)2
ab(a2n + b2n + 2anbn) = a2n + 2 + b2n + 2 + 2a2n + 2 b2n + 2
a2n+1b + ab2n+1 + 2an+1bn+1 = a2n + 2 + b2n + 2 + 2a2n + 2 b2n + 2
ba2n+1 + ab2n+1 = a2n + 2 + b2n + 2
ab2n+1 – b2n + 2 = a2n + 2 – ba2n+1
ab2n+1 – b2n + 2 = a2n + 2 – ba2n+1
b2n+1 (a – b) = a2n + 1(a – b)
b2n+1 = a2n + 1
a2n+1 / b2n + 1 = 1 = (a/b)0
(a/b)2n + 1 = 1 = (a/b)0
2n + 1 = 0
n = -1/2
Question 28. The sum of two numbers is 6 times their geometric mean, show that numbers are in the ratio 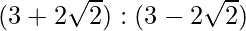
Solution:
Let the two numbers be a and b.
And G.M. = √ab
According to the question
a + b = 6√ab …..(1)
Squaring on both side, we get
(a + b)2 = 36(ab)
As we know that
(a – b)2 = (a + b)2 – 4(ab)
So,
(a – b)2 = 36(ab) – 4(ab)
a – b = 4√2√ab ……(2)
Now we add eq(a) and (2), we get
a + b + a – b = 6√ab + 4√2√ab
2a = √ab(6 + 4√2)
a = √ab(3 + 2√2)
Now put the value of a in eq(1), we get the value of b
√ab(3 + 2√2) + b = 6√ab
b = √ab(3 – 2√2)
Now we find the ratio:
a/b = √ab(3 + 2√2)/√ab(3 – 2√2)
= (3 + 2√2)/(3 – 2√2)
Question 29. If A and G be A.M. and G.M., respectively between two positive numbers, prove that the numbers are 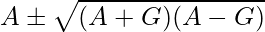
Solution:
Let the two numbers be a & b.
A.M = A= (a + b)/2
G.M = G = 2/√ab
So, a + b = 2A ….(1)
G2 = ab ….(2)
As we know that
(a – b)2 = (a + b)2 – 4(ab)
So,
(a – b)2 = (2A)2 – 4(G2)
(a – b)2 = 4(A)2 – 4(G2)
(a – b)2 = 4[(A)2 – (G2)]
(a – b)2 = 4[(A – G)(A + G)]
(a – b) = √4[(A – G)(A + G)]
(a – b) = 2√(A – G)(A + G) ……(3)
Now add eq(1) and (3), we get
2a = 2A + 2√(A – G)(A + G)
a = A + √(A – G)(A + G)
Now put the value of a in eq(1), we get
A + √(A – G)(A + G) + b = 2A
b = A – √(A – G)(A + G)
Hence, the two numbers are A ± √(A – G)(A + G)
Question 30. The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour, and nth hour?
Solution:
As the count of bacteria doubles after each hour, so at the end of n hours it becomes 2n times the original count.
So, first term(a) = 30, and common ratio(r) = 2
So, a3 = ar2 = (30)(2)2 = 120
At the end of 2nd hour there are 120 bacteria.
a4 = ar4 = (30)(2)4 = 480
At the end of 4nd hour there are 480 bacteria.
an+1 = arn = (30)(2)n
At the end of nnd hour there are (30)(2)n bacteria.
Question 31. What will Rs. 500 amounts to in 10 years after its deposit in a bank which pays an annual interest rate of 10% compounded annually?
Solution:
In the end of 1st year, the amount = 500(1 + 1/10) = 500(1.1)
In the end of 2nd year, the amount = 500(1.1)(1.1)
In the end of 3rd year, the amount = 500(1.1)(1.1)(1.1)
…..So on
At the end of 10 year, the amount = 500(1.1)(1.1)(1.1)…….10 times
= 500(1.1)10
Question 32. If A.M. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtain the quadratic equation.
Solution:
Let the roots of the quadratic equation be a and b.
According to the question
A.M. = (a + b)/2 = 8
a + b = 16
G.M. = √ab = 5
ab = 25
Then the quadratic equation using the roots can be written as
x2 – (a + b)x + ab = 0
Now put all these values in the quadratic equation, we get
x2 – 16x + 25 = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...