Question 1. How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER?
Solution:
In the word “DAUGHTER”, there are 3 vowels, namely, A, U, E, and 5 consonants, namely, D, G, H, T, R.
The number of ways of selecting 2 vowels out of 3 = 3C2 = 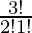 = 3.
= 3.
The number of ways of selecting 3 consonants out of 5 = 5C3 = 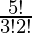 =10.
=10.
Therefore, the number of combinations of 2 vowels and 3 consonants is 3 x 10 = 30.
Now, each of these 30 combinations has 5 letters which can be arranged among themselves in 5! ways.
Therefore, the required number of different words is 30 x 5! = 30 x 120 = 3600
Question 2. How many words, with or without meaning, can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?
Solution:
There are 8 different letters in the word “EQUATION”, in which there are 5 vowels, namely, A, E, I, O and U and 3 consonants, namely, Q, T and N. Since the vowels and consonants have to occur together, assume all vowels as one object (AEIOU) and all consonants as another (QTN). So, there are 2 objects now.
Then, permutations of these 2 objects taken all at a time = 2P2 = 2! =2.
Within vowel group, we have 5! Possible permutations and 3! permutations within the consonants group.
Hence, the required number of permutations = 2! x 5! x 3! = 1440.
Question 3. A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of: (i) exactly 3 girls ? (ii) atleast 3 girls ? (iii) atmost 3 girls ?
Solution:
(i) We have to select 7 members from 13 (9 boys + 4 girls).
If there are exactly 3 girls in each combination, then
The number of ways of selecting 3 girls out of 4 = 4C3 = 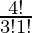 = 4
= 4
The number of ways of selecting 4 boys out of 9 = 9C4 = 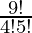 = 126
= 126
Hence, total number of ways to form committee with exactly 3 girls = 126 x 4 = 504
(ii) Since, the team has to consist of at least 3 girls, the team can consist of
3 girls and 4 boys, or 4 girls and 3 boys.
Case 1: The team can consist of 3 girls and 4 boys:
So, from(i), we have,
Total number of ways to select 3 girls and 4 boys = 126 x 4 = 504
Case 2: The team can consist of 4 girls and 3 boys:
Total number of ways to select 4 girls and 3 boys = 4C4 x 9C3 = 1 x 84 = 84
Therefore, total number of ways to form a committee with at least 3 girls = 504 + 84 = 588
(iii) Since, the team has to consist of at most 3 girls, the team can consist of
3 girls and 4 boys, or 2 girls and 5 boys, or 1 girl and 6 boys, or 7 boys
Case 1: The team can consist of 3 girls and 4 boys
Total number of ways to select 3 girls and 4 boys = 126 x 4 = 504
Case 2: The team can consist of 2 girls and 5 boys
Total number of ways to select 2 girls and 5 boys = 4C2 x 9C5 =  = 126 x 6 = 756
= 126 x 6 = 756
Case 3: The team can consist of 1 girl and 6 boys
Total number of ways to select 1 girl and 6 boys = 4C1 x 9C6 =  = 84 x 4 = 336
= 84 x 4 = 336
Case 4: The team can consist of 7 boys
The number of ways of selecting 7 boys out of 9 = 9C7 = 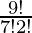 = 36
= 36
Therefore, total number of ways to form a committee with at most 3 girls = 504 + 756 + 336 + 36 = 1632
Question 4. If the different permutations of all the letter of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E?
Solution:
In a dictionary, words are in ascending order. Hence, for this scenario, all the words starting with A will come before first word starting with E.
To get the number of words starting with A, we fix the letter A at the extreme left position and then rearrange the remaining 10 letters taken all at a time. These 10 letters includes I and N 2 times.
Hence, the number of words starting with A = 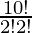 = 907200.
= 907200.
Hence, 907200 words are there in the list before the first word starting with E.
Question 5. How many 6-digit numbers can be formed from the digits 0, 1, 3, 5, 7, and 9 which are divisible by 10, and no digit is repeated?
Solution:
We know that, a number is divisible by 10 if it has 0 at its unit place. Hence, 0 will be fixed at last place in a number.
The remaining 5 places can be filled by any digit 1, 3, 5, 7 or 9. These 5 digits can be arranged at 5 places in 5P5 = 5! ways.
Hence, 6-digit numbers that can be formed which are divisible by 10 = 5! = 120.
Question 6. The English alphabet has 5 vowels and 21 consonants. How many words with two different vowels and 2 different consonants can be formed from the alphabet?
Solution:
We have to select 2 vowels from 5 and 2 consonants from 21.
The number of ways to select 2 vowels from 5 = 5C2 =  = 10
= 10
The number of ways to select 2 consonants from 21 = 21C2 = 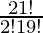 = 210
= 210
Permutations of these 4 alphabets taken all at a time = 4P4 = 4! = 24.
Hence, number of words can be formed with 2 different vowels and 2 different consonants = 10 x 210 x 24 = 50400
Question 7. In an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?
Solution:
Since, it is required to attempt at least 3 questions from each part, questions selection can be
Case 1: (3, 5), or (b)(4, 4), or (c) (5, 3) ……(Part I questions, Part 2 questions)
Part I consists of 5 questions and Part II consists of 7 questions.
So, Number of ways to select 3 questions from Part I = 5C3 = 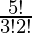 = 10
= 10
Number of ways to select 5 questions from Part II = 7C5 = 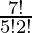 = 21
= 21
Hence, total number of ways for this type of question selection = 10 x 21 = 210
Case 2: Number of ways to select 4 questions from Part I = 5C4 = 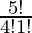 = 5
= 5
Number of ways to select 4 questions from Part II = 7C4 = 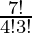 = 35
= 35
Hence, total number of ways for this type of question selection = 5 x 35 = 175
Case 3: Number of ways to select 5 questions from Part I = 5C5 = 1
Number of ways to select 3 questions from Part II = 7C3 = 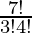 = 35
= 35
Hence, total number of ways for this type of question selection = 1 x 35 = 35
Therefore, a student can select the questions in 210 + 175 + 35 = 420 ways.
Question 8. Determine the number of 5-card combinations out of a deck of 52 cards if each selection of 5 cards has exactly one king.
Solution:
We have to select 5 cards from 52 cards. If there is exactly one king in each combination, then
Case 1: We have to select 1 king card from 4 king cards
Number of ways to select king card = 4C1 =  = 4
= 4
Case 2: We have to select 5 – 1 = 4 cards from remaining 52 – 4 = 48 cards
Number of ways to select remaining 4 cards = 48C4 = 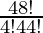 = 194580
= 194580
And, hence required total number of 5 card combinations = 4 x 194580 = 778320.
Question 9. It is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible?
Solution:
There are 5 men and 4 women. Women occupy the even places. Hence, the possible seating arrangement of men and women will be MWMWMWMWM where M denotes Man and W denotes Woman.
Now, 4 women can occupy 4 even places in 4P4 = 4! ways.
And, 5 men can occupy 5 odd places in 5P5 = 5! ways.
Hence, Total number of such possible arrangements:
5! x 4! = 5 x 4 x 3 x 2 x 1 x 4 x 3 x 2 x 1 = 2880.
Question 10. From a class of 25 students, 10 are to be chosen for an excursion party. There are 3 students who decide that either all of them will join or none of them will join. In how many ways can the excursion party be chosen?
Solution:
According to those 3 students who decide to either join all of them or join none of them, there are 2 cases for excursion party member selection:
Case 1: Do not select those 3 students.
Hence, select 10 students from remaining 25 – 3 = 22 students.
The number of ways to do this = 22C10 = 646646
Case 2: Select those 3 students.
This means, we are short of 7 students and these can be selected from remaining 25 – 3 = 22 students.
The number of ways to do this = 22C7 x 3C3 = 170544
Hence, required number of ways to choose excursion party:
646646 + 170544 = 817190
Question 11. In how many ways can the letters of the word ASSASSINATION be arranged so that all the S’s are together?
Solution:
Word “ASSASSINATION” has 4 S. We have to place all S’s together. Hence, we will assume group of 4 S as a single object. This single object together with 9 remaining letters (objects) will be counted as 10 objects to be arranged. These include 3 A’s, 2 I’s and N’s and 1 T and O.
So, required number of ways = 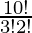 = 151200
= 151200
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...