Class 11 NCERT Solutions- Chapter 5 Complex Numbers And Quadratic Equations – Exercise 5.1 | Set 1
Last Updated :
05 Apr, 2021
For Q.1 to Q.10 express each complex number in form of a+ib
Question 1. (5i)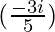
Solution:
Let the given number be a,
a= (5i)*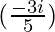
a= 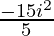
a= (-3)*i2
a= (-3)*(-1)
a= 3+0i
Question 2. i9+i19
Solution:
Let the given number be a,
a = i9 * (1+i10)
a = ((i4)2*i )(1 + (i4)2 (i2))
a = (1*i)(1+i2)
a = (i)*(0)
a = 0+0i
Question 3. i-39
Solution:
Let the given number be a and let z = i39 ,
z = (i)*(i2)19
z = (i)*(-1)19
z = -i
a = i-39
a = 1/i39
a = 1/z
a = 1/-i
a = (i4)/-i
a = -i3 = -(i2*i)
a = -1*-i
a = 0+i
Question 4. 3(7+7i) + i(7+7i)
Solution:
Let the given number be a,
a = 3*(7+7i)+i*(7+7i)
a = 21+21i+7i+7i2
a = 21+7i2+28i
a = 21-7+28i
a = 14+28i
Question 5. (1-i)-(-1+i6)
Solution:
Let the given number be a,
a = (1-i)-(-1+6i)
a = 1-i+1-6i
a = 2-7i
Question 6. (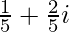 )-(4+
)-(4+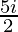 )
)
Solution:
Let the given number be a,
a = 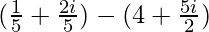
a = 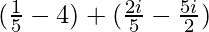
a = 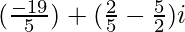
a = (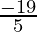 )+(
)+(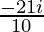 )
)
a =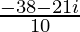
Question 7. [(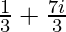 )+(4+
)+(4+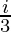 ]-(
]-(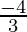 +i)
+i)
Solution:
Let the given number be a,
a = (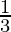 +
+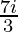 )+(4+
)+(4+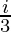 )-(
)-(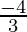 +i)
+i)
a = (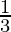 +4+
+4+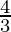 )+(
)+(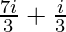 -i)
-i)
a = (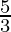 +4)+(
+4)+(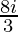 -i)
-i)
a = 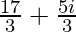
a = 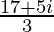
Question 8. (1-i)4
Solution:
Let the given number be a,
a = ((1-i)2)2
As we know , (a-b)2= (a2+b2-2ab)
a = (1+i2-2i)2
a = (1-1-2i)2
a = (-2i)2
a = 4i2
a = -4+0i
Question 9. (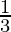 +3i)3
+3i)3
Solution:
Let the given number be a,
a = (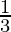 +3i)3
+3i)3
As we know, (a+b)3= (a3+b3+3ab(a+b))
a = ((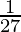 )+(3i)3 +3(
)+(3i)3 +3(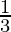 )*(3i)(
)*(3i)(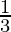 +3i))
+3i))
a = (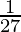 +(-27i)+ 3i*(
+(-27i)+ 3i*(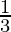 +3i))
+3i))
a = (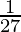 +(-27i)+i+9i2)
+(-27i)+i+9i2)
a = ((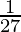 )-9+(-27)i+i)
)-9+(-27)i+i)
a = ((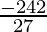 )-26i)
)-26i)
Question 10. (-2-(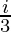 ))3
))3
Solution:
Let the given number be a,
a = (-2-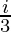 )3
)3
a = -((2+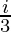 )3)
)3)
As we know, (a+b)3= (a3+b3+3ab(a+b))
a = -((8)+(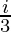 )3 +3(2)*(
)3 +3(2)*(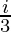 )(2+
)(2+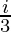 ))
))
a = -(8+(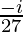 )+ 2i*(2+
)+ 2i*(2+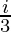 ))
))
a = -(8-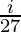 +4i+
+4i+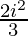 )
)
a = -(8-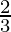 +(
+(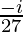 )+4i)
)+4i)
a = -(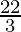 +(
+(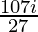 ))
))
a = 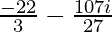
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...