Class 11 NCERT Solutions- Chapter 3 Trigonometric Function – Exercise 3.3 | Set 2
Last Updated :
07 Apr, 2021
Question 15: cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
Solution:
Taking LHS in consideration, we get
= cot 4x (sin 5x + sin 3x)
=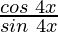 (sin 5x + sin 3x)
(sin 5x + sin 3x)
Using the identity,
sin A + sin B = 2 sin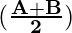 cos
cos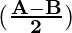
=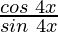 (2 sin
(2 sin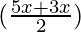 cos
cos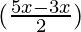 )
)
=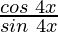 (2 sin
(2 sin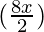 cos
cos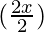 )
)
=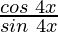 (2 sin 4x cos x)
(2 sin 4x cos x)
= 2 cos 4x cos x
Now, taking RHS in consideration, we get
= cot x (sin 5x – sin 3x)
=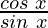 (sin 5x – sin 3x)
(sin 5x – sin 3x)
Using the identity,
sin A – sin B = 2 cos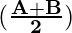 sin
sin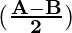
=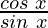 (2 cos
(2 cos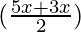 sin
sin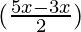 )
)
=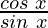 (2 cos
(2 cos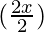 sin
sin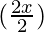 )
)
=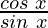 (2 cos 4x sin x)
(2 cos 4x sin x)
= 2 cos 4x cos x
Hence, LHS = RHS
Question 16: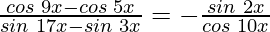
Solution:
Taking LHS in consideration, we get
=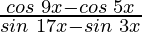
Using the identity,
cos A – cos B = 2 sin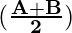 sin
sin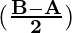
sin A – sin B = 2 cos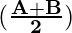 sin
sin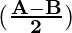
=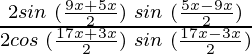
=
=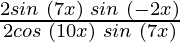
=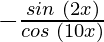
Hence, LHS = RHS
Question 17: = tan 4x
= tan 4x
Solution:
Taking LHS in consideration, we get
=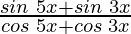
Using the identity,
sin A + sin B = 2 sin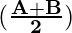 cos
cos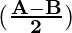
cos A + cos B = 2 cos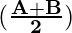 cos
cos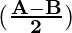
=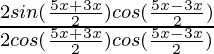
=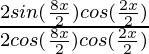
=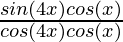
=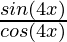
= tan 4x
Hence, LHS = RHS
Question 18: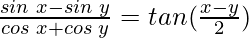
Solution:
Taking LHS in consideration, we get
=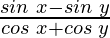
Using the identity,
sin A – sin B = 2 cos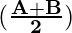 sin
sin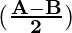
cos A + cos B = 2 cos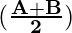 cos
cos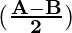
=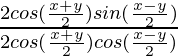
=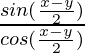
=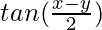
Hence, LHS = RHS
Question 19: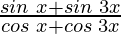 = tan 2x
= tan 2x
Solution:
Taking LHS in consideration, we get
=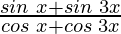
Using the identity,
sin A + sin B = 2 sin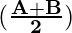 cos
cos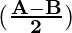
cos A + cos B = 2 cos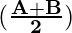 cos
cos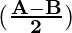
=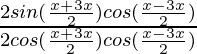
=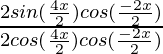
=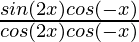
=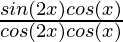
=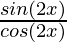
= tan 2x
Hence, LHS = RHS
Question 20: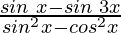 = 2 sin x
= 2 sin x
Solution:
Taking LHS in consideration, we get
=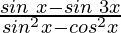
Using the identity,
sin A – sin B = 2 cos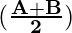 sin
sin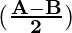
cos 2θ = cos2 θ – sin2 θ
=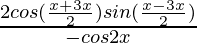
=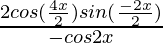
=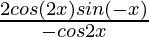
=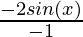
= 2 sin (x)
Hence, LHS = RHS
Question 21: = cot 3x
= cot 3x
Solution:
Taking LHS in consideration, we get
=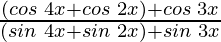
Using the identity,
sin A + sin B = 2 sin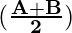 cos
cos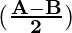
cos A + cos B = 2 cos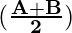 cos
cos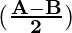
=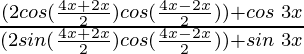
=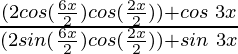
=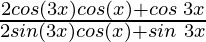
Taking common, we have
=![Rendered by QuickLaTeX.com \frac{cos (3x) [2 cos (x)+1]}{sin (3x)[2cos (x)+1]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6611a474ab50922308f977bc864daf3a_l3.png)
=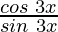
= cot 3x
Hence, LHS = RHS
Question 22: cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1
Solution:
Taking LHS in consideration, we get
= cot x cot 2x – cot 2x cot 3x – cot 3x cot x
= cot x cot 2x – cot 3x (cot 2x + cot x)
= cot x cot 2x – cot (2x+x) (cot 2x + cot x)
Using the identity,
cot(A+B) =
= cot x cot 2x –![Rendered by QuickLaTeX.com [\frac{cot 2x \hspace{0.1cm}cot x - 1}{cot 2x + cot x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ddeb8e2899ef3005873c35ee99b5550c_l3.png) (cot 2x + cot x)
(cot 2x + cot x)
= cot x cot 2x – [cot 2x cot x – 1]
= cot x cot 2x – cot 2x cot x – 1
= 1
Hence, LHS = RHS
Question 23: tan 4x =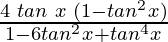
Solution:
Taking LHS in consideration, we get
tan 4x = tan 2(2x)
Using the identity,
tan 2θ =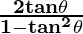
=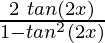
Again using the same identity, we get
=
=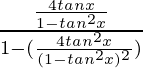
=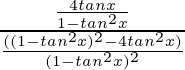
=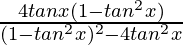
=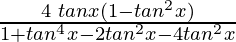
=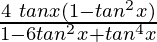
Hence, LHS = RHS
Question 24: cos 4x = 1 – 8sin2x cos2x
Solution:
Taking LHS in consideration, we get
cos 4x = cos 2 (2x)
Using the identity,
cos 2θ = 1 – 2sin2 θ
= 1 – 2sin2 (2x)
= 1 – 2(2sin x cos x)2 (As, sin 2θ = 2 sin θ cos θ)
= 1 – 2(4sin2 x cos2 x)
= 1 – 8sin2 x cos2 x
Hence, LHS = RHS
Question 25: cos 6x = 32 cos6x – 48cos4x + 18 cos2x – 1
Solution:
Taking LHS in consideration, we get
cos 6x = cos 3 (2x)
Using the identity,
cos 3θ = 4 cos3 θ – 3 cos θ
= 4 cos3 (2x) – 3 cos (2x)
= 4 cos3 (2x) – 3 cos (2x)
Now, Using the identity cos 2θ = 2cos2 θ – 1
= 4 (2cos2 x – 1)3 – 3 (2cos2 x – 1)
Using algebraic identity,
(a-b)3 = a3 + b3 – 3a2b + 3ab2
= 4 [(2 cos2 x) 3 – (1)3 – 3 (2 cos2 x) 2 + 3 (2 cos2 x)(1)2] – 6cos2 x + 3
= 4 [8cos6x – 1 – 12 cos4x + 6 cos2x] – 6 cos2x + 3
= 32 cos6x – 4 – 48 cos4x + 24 cos2 x – 6 cos2x + 3
= 32 cos6x – 48 cos4x + 18 cos2x – 1
Hence, LHS = RHS
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...