Class 11 NCERT Solutions- Chapter 13 Limits And Derivatives – Miscellaneous Exercise on Chapter 13 | Set 2
Last Updated :
30 Apr, 2021
Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Question 16: 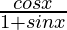
Solution:
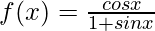
Taking derivative both sides,
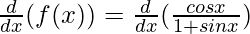
Using the quotient rule, we have
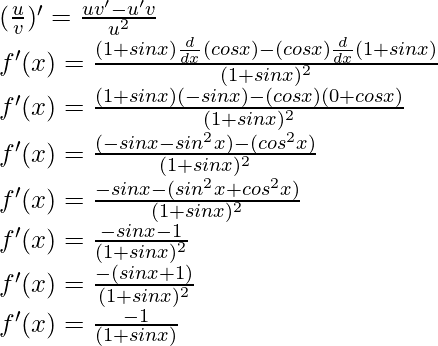
Question 17: 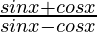
Solution:
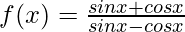
Taking derivative both sides,
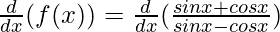
Using the quotient rule, we have
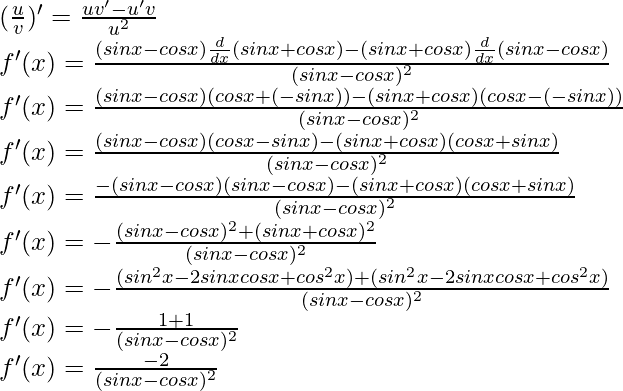
Question 18: 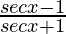
Solution:
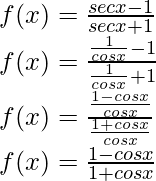
Taking derivative both sides,
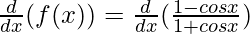
Using the quotient rule, we have
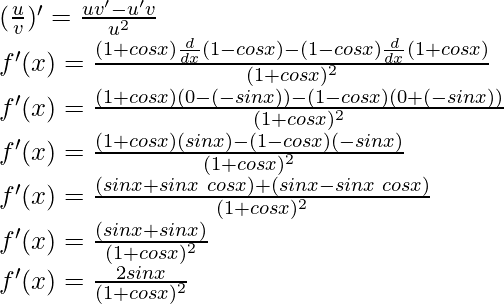
Question 19: sinn x
Solution:
f(x) = sinn x
When n = 1,
f(x) = sin x
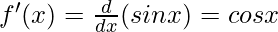
When n = 2,
f(x) = sin2 x = sin x sin x
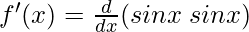
Using the product rule, we have
(uv)’ = uv’+vu’
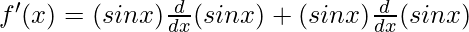
f'(x) = (sin x) (cos x) + (sin x) (cos x) = 2 sin x cos x
When n = 3,
f(x) = sin3 x = sin2 x sin x
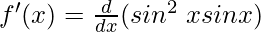
Using the product rule, we have
(uv)’ = uv’+vu’
![Rendered by QuickLaTeX.com f'(x) = (sin^2 x) \frac{d}{dx}(sin x) + (sin x) \frac{d}{dx}(sin^2 x)\\ f'(x) = (sin^2 x) (cos x) + (sin x) (2 sin x\hspace{0.1cm} cos x)\\ f'(x) = (sin^2 x \hspace{0.1cm}cos x) + (2 sin^2 x \hspace{0.1cm}cos x)\\ f'(x) = (sin^2 x\hspace{0.1cm} cos x)[1+2]\\ f'(x) = 3 sin^2 x \hspace{0.1cm}cos x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7318a781107414de49f8b50281887a40_l3.png)
Pattern w.r.t n is seen here, as follows
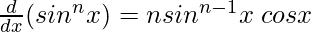
Let’s check this statement.
For P(n) = n sinn-1x cos x
For P(1),
P(1) = 1 sin1-1x cos x = cos x. Which is true.
n=k
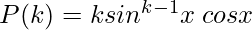
n = k+1
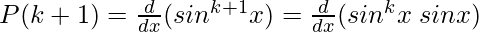
Using the product rule, we have
(uv)’ = uv’+vu’
= (sink x) 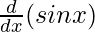 + (sin x)
+ (sin x) 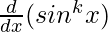
= (sink x) (cos x) + (sin x) (k sink-1 x cos x)
= (sink x) (cos x)[k+1]
Hence proved for P(k+1).
So,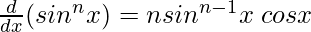 is true.
is true.
Question 20: 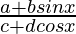
Solution:
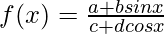
Taking derivative both sides,
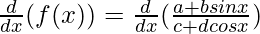
Using the quotient rule, we have
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-u'v}{u^2}\\ f'(x) = \frac{(c+dcos x) \frac{d}{dx}(a+bsin x) - (a+bsin x)\frac{d}{dx}(c+dcos x)}{(c+dcos x)^2}\\ f'(x) = \frac{(c+dcos x) [\frac{d}{dx}(a)+\frac{d}{dx}(bsin x)] - (a+bsin x)\frac{d}{dx}(c)+\frac{d}{dx}(dcos x)}{(c+dcos x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b385a146653a12a77170fd1f7540fe6a_l3.png)
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = \frac{(c+dcos x) [0+b cos x] - (a+bsin x)[0+(-d sin x)]}{(c+dcos x)^2}\\ f'(x) = \frac{(c+dcos x) (b cos x) + (a+bsin x)(d sin x)}{(c+dcos x)^2}\\ f'(x) = \frac{(bc\hspace{0.1cm} cos x+db\hspace{0.1cm} cos^2 x) + (ad\hspace{0.1cm} sin x+db\hspace{0.1cm} sin^2 x)}{(c+d\hspace{0.1cm}cos x)^2}\\ f'(x) = \frac{(bc\hspace{0.1cm} cos x + db (cos^2 x + sin ^2 x) + ad \hspace{0.1cm}sin x)}{(c+d\hspace{0.1cm}cos x)^2}\\ f'(x) = \frac{(bc\hspace{0.1cm} cos x + db+ ad\hspace{0.1cm} sin x)}{(c+d\hspace{0.1cm}cos x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46bd8855bec22fa2d46a628c4dbe310b_l3.png)
Question 21: 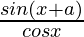
Solution:
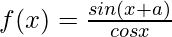
Taking derivative both sides,
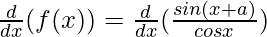
Using the quotient rule, we have
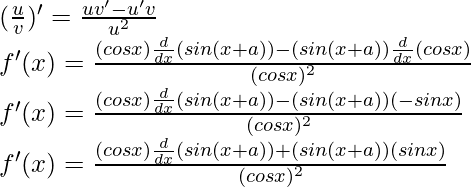
Let’s take g(x) = sin (x+a)
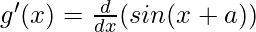
g(x+h) = sin((x+h)+a)
From the first principle,
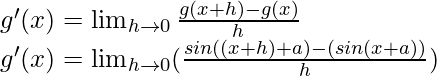
Using the trigonometric identity,
sin A – sin B = 2 cos 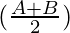 sin
sin 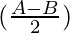
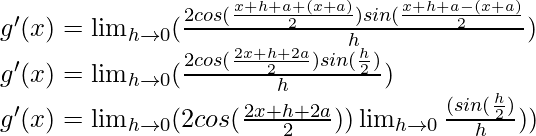
Multiply and divide by 2, we have
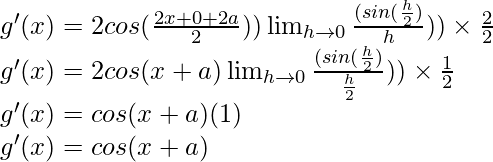
Hence,
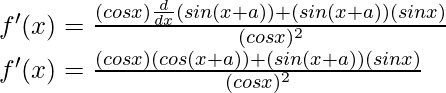
Using the trigonometric identity,
cos A cos B + sin A sin B = cos (A-B)
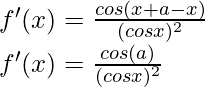
Question 22: x4(5sin x – 3cos x)
Solution:
f(x) = x4 (5sin x – 3cos x)
Taking derivative both sides,
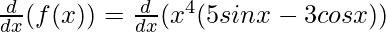
Using the product rule, we have
(uv)’ = uv’ + vu’
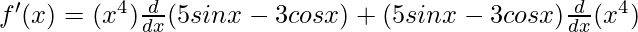
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = (x^4) [\frac{d}{dx}(5sin x) - \frac{d}{dx}(3cos x)] + (5sin x - 3cos x)(4x^{4-1})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2e279f80af5126ccb69847e3249901ef_l3.png)
f'(x) = (x4) [(5 cos x) – (3 (- sin x))] + (5sin x – 3cos x)(4x3)
f'(x) = (x4) [(5 cos x) + (3 sin x)] + (5sin x – 3cos x)(4x3)
f'(x) = (x3) [5x cos x + 3x sin x + 20sin x – 12 cos x]
Question 23: (x2+1) cos x
Solution:
f(x) = (x2+1) cos x
Taking derivative both sides,
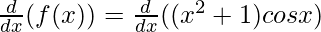
Using the product rule, we have
(uv)’ = uv’ + vu’
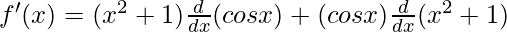
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = (x^2+1) (- sin x) + (cos x)[\frac{d}{dx}(x^2)+\frac{d}{dx}(1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f3013b844762fa157272313176aa37fc_l3.png)
f'(x) = (x2+1) (- sin x) + (cos x)[(2x2-1)+0]
f'(x) = -x2 sin x- sin x + 2x cos x
Question 24: 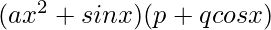
Solution:
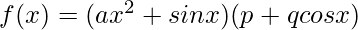
Taking derivative both sides,
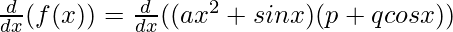
Using the product rule, we have
(uv)’ = uv’ + vu’
![Rendered by QuickLaTeX.com f'(x) = (ax^2+sin x) \frac{d}{dx}(p+q cos x) + (p+q cos x)\frac{d}{dx}((ax^2+sin x))\\ f'(x) = (ax^2+sin x) [\frac{d}{dx}(p)+\frac{d}{dx}(q cos x)] + (p+q cos x)[\frac{d}{dx}(ax^2)+\frac{d}{dx}(sin x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ad2ca3a846a021eeace67eccf1bc6e1_l3.png)
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = (ax^2+sin x) [0+q(- sin x)] + (p+q cos x)[a(2x^{2-1})+(cos x)]\\ f'(x) = (ax^2+sin x) (- q sin x) + (p+q cos x)[2ax+cos x]\\ f'(x) = - q sin x(ax^2 + sin x) + (p+q cos x)[2ax+cos x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d74156a985e6824124fdb882a135d9dc_l3.png)
Question 25: (x + cos x)(x – tan x)
Solution:
f(x) = (x + cos x)(x – tan x)
Taking derivative both sides,
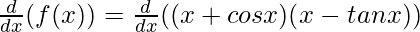
Using the product rule, we have
(uv)’ = uv’ + vu’
![Rendered by QuickLaTeX.com f'(x) = (x + cos x) \frac{d}{dx}(x - tan x) + (x - tan x)\frac{d}{dx}(x + cos x)\\ f'(x) = (x + cos x) [\frac{d}{dx}(x) - \frac{d}{dx}(tan x)] + (x - tan x)[\frac{d}{dx}(x) + \frac{d}{dx}(cos x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6ef2bab372d3afe1d311ed812d337b58_l3.png)
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = (x + cos x) [1 - \frac{d}{dx}(tan x)] + (x - tan x)[1 + (- sin x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5d574cc91777a5a6fc42f96fad014e12_l3.png)
Let’s take g(x) = tan x
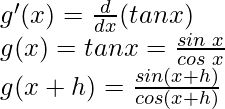
From the first principle,
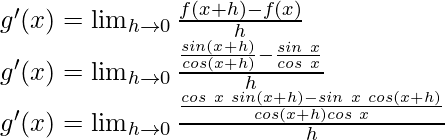
Using the trigonometric identity,
sin a cos b – cos a sin b = sin (a-b)
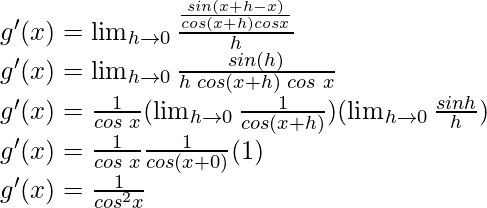
g'(x) = sec2x
Hence,
f'(x) = (x + cos x) ![Rendered by QuickLaTeX.com [1 - \frac{d}{dx}(tan x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e187ceba1a96709a5182b64f8aea566e_l3.png) + (x – tan x)[1 + (- sin x)]
+ (x – tan x)[1 + (- sin x)]
f'(x) = (x + cos x) [1 – (sec2 x)] + (x – tan x)[1 – sin x]
f'(x) = (x + cos x) [tan2 x] + (x – tan x)[1 – sin x]
f'(x) = tan2 x(x + cos x) + (x – tan x)[1 – sin x]
Question 26: 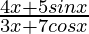
Solution:
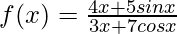
Taking derivative both sides,
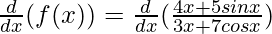
Using the quotient rule, we have
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-u'v}{u^2}\\ f'(x) = \frac{(3x+7cos x) \frac{d}{dx}(4x+5sin x) - (4x+5sin x)\frac{d}{dx}(3x+7cos x)}{(3x+7cos x)^2}\\ f'(x) = \frac{(3x+7cos x) [\frac{d}{dx}(4x)+\frac{d}{dx}(5sin x)] - (4x+5sin x)[\frac{d}{dx}(3x)+\frac{d}{dx}(7cos x)]}{(3x+7cos x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b2551887531c708c54d6ab99107e0c97_l3.png)
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = \frac{(3x+7cos x) [4+(5 cos x)] - (4x+5sin x)[3 + 7(- sin x)]}{(3x+7cos x)^2}\\ f'(x) = \frac{(3x+7cos x) [4+5 cos x] - (4x+5sin x)[3 - 7 sin x]}{(3x+7cos x)^2}\\ f'(x) = \frac{(12x+28 cos x+15x cos x + 35 cos^2x) - [(12x + 15sin x)-(28x sin x + 35 sin^2 x)]}{(3x+7cos x)^2}\\ f'(x) = \frac{(12x+28 cos x+15x cos x + 35 cos^2x)- (12x + 15sin x-28x sin x - 35 sin^2 x)}{(3x+7cos x)^2}\\ f'(x) = \frac{(12x+28 cos x+15x cos x + 35 cos^2x - 12x - 15sin x+28x sin x + 35 sin^2 x)}{(3x+7cos x)^2}\\ f'(x) = \frac{(28 cos x+15x cos x + 35 (cos^2x + sin^2x) - 15sin x + 28x sin x)}{(3x+7cos x)^2}\\ f'(x) = \frac{(28 cos x+15x cos x + 35 - 15sin x + 28x sin x)}{(3x+7cos x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d6262ca65e274d5f9288b4302ad1a7f9_l3.png)
Question 27: 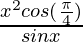
Solution:
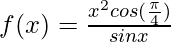
Taking derivative both sides,
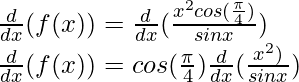
Using the quotient rule, we have
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-u'v}{u^2}\\ f'(x) = (cos(\frac{\pi}{4}) [\frac{(sin x) \frac{d}{dx}(x^2) - (x^2)\frac{d}{dx}(sin x)}{(sin x)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4630855cb1ab1f6fcec8480e6b85e449_l3.png)
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = cos(\frac{\pi}{4}) [\frac{(sin x) (2x^{2-1}) - (x^2) (cos x)}{(sin x)^2}]\\ f'(x) = cos(\frac{\pi}{4}) [\frac{2x sin x - x^2 cos x)}{(sin x)^2}]\\ f'(x) = [\frac{(x cos(\frac{\pi}{4})(2 sin x - x cos x)}{(sin x)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b6c5c2fdd80b09687c0d4eee25c41f1_l3.png)
Question 28: 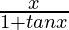
Solution:
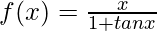
Taking derivative both sides,
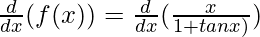
Using the quotient rule, we have
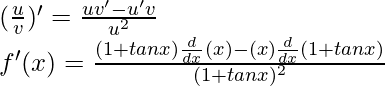
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = \frac{(1+tan x) (1) - (x)[\frac{d}{dx}(1)+\frac{d}{dx}(tan x)]}{(1+tan x)^2}\\ f'(x) = \frac{(1+tan x) - (x)[0+\frac{d}{dx}(tan x)]}{(1+tan x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a1e4edc5163be4ad89497e7813626b9_l3.png)
Let’s take g(x) = tan x
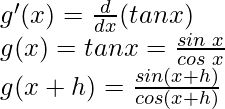
From the first principle,
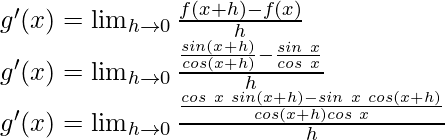
Using the trigonometric identity,
sin a cos b – cos a sin b = sin (a-b)
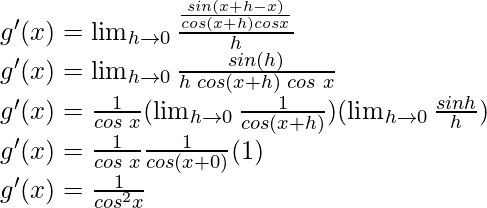
g'(x) = sec2x
Hence, ![Rendered by QuickLaTeX.com f'(x) = \frac{(1+tan x) - (x)[0+\frac{d}{dx}(tan x)]}{(1+tan x)^2}\\ f'(x) = \frac{1+tan x - x sec^2x}{(1+tan x)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-afc6b8b8ed22828c52bd691f1f27dba5_l3.png)
Question 29: (x + sec x) (x-tan x)
Solution:
f(x) = (x + sec x) (x-tan x)
Taking derivative both sides,
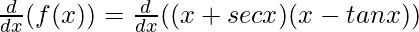
Using the product rule, we have
(uv)’ = uv’ + vu’
![Rendered by QuickLaTeX.com f'(x) = (x + sec x) \frac{d}{dx}(x - tan x) + (x - tan x)\frac{d}{dx}(x + sec x)\\ f'(x) = (x + sec x) [\frac{d}{dx}(x) - \frac{d}{dx}(tan x)] + (x - tan x)[\frac{d}{dx}(x) + \frac{d}{dx}(sec x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3246e6877fa563cac5371c851d22e966_l3.png)
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = (x + sec x) [1 - \frac{d}{dx}(tan x)] + (x - tan x)[1 + \frac{d}{dx}(sec x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b0a8b06e7c2586ea2a48aec8fbeead49_l3.png)
Let’s take g(x) = tan x
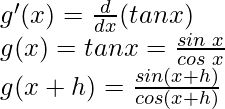
From the first principle,
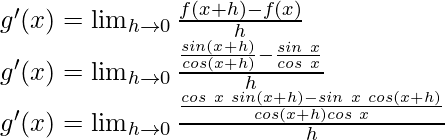
Using the trigonometric identity,
sin a cos b – cos a sin b = sin (a-b)
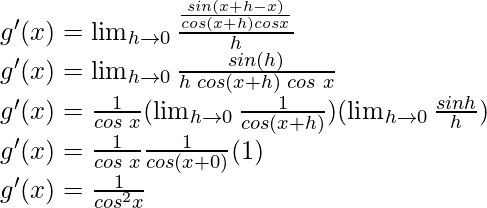
g'(x) = sec2x
Now, let’s take h(x) = sec x = 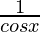
h(x+h) =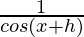
From the first principle,
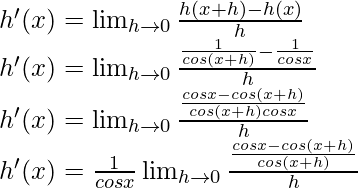
Using the trigonometric identity,
cos a – cos b = -2 sin 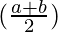 sin
sin 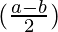
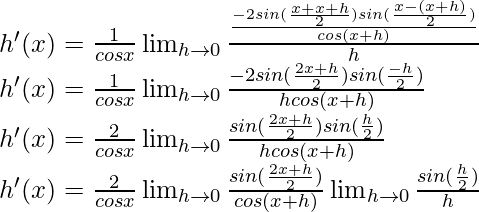
Multiply and divide by 2, we have
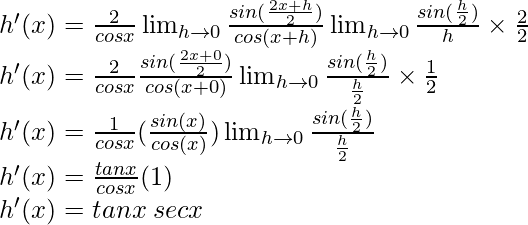
Hence, ![Rendered by QuickLaTeX.com f'(x) = (x + sec x) [1 - \frac{d}{dx}(tan x)] + (x - tan x)[1 + \frac{d}{dx}(sec x)]\\ f'(x) = (x + sec x) [1 - (sec^2x)] + (x - tan x)[1 + (sec x \hspace{0.1cm}tan x)]\\ f'(x) = (x + sec x) [tan^2x)] + (x - tan x)[1 + (sec x \hspace{0.1cm}tan x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a95429721ec241fbe6034284cb43d171_l3.png)
Question 30: 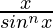
Solution:
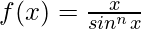
Taking derivative both sides,
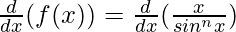
Using the quotient rule, we have
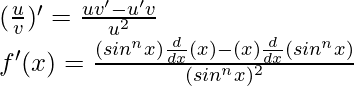
As, the derivative of xn is nxn-1 and derivative of constant is 0.
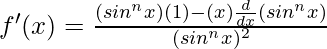
Let’s take, g(x) = sinn x
When n = 1,
g(x) = sin x
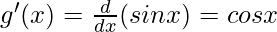
When n = 2,
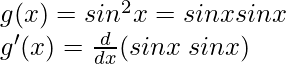
Using the product rule, we have
(uv)’ = uv’+vu’
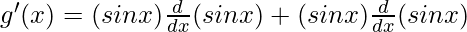
g'(x) = (sin x) (cos x) + (sin x) (cos x) = 2 sin x cos x
When n = 3,
g(x) = sin3 x = sin2 x sin x
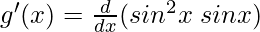
Using the product rule, we have
(uv)’ = uv’+vu’
![Rendered by QuickLaTeX.com g'(x) = (sin^2 x) \frac{d}{dx}(sin x) + (sin x) \frac{d}{dx}(sin^2 x)\\ g'(x) = (sin^2 x) (cos x) + (sin x) (2 sin x \hspace{0.1cm}cos x)\\ g'(x) = (sin^2 x \hspace{0.1cm}cos x) + (2 sin^2 x\hspace{0.1cm} cos x)\\ g'(x) = (sin^2 x\hspace{0.1cm} cos x)[1+2]\\ g'(x) = 3 sin^2 x\hspace{0.1cm} cos x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0f6118724449ba9d0dba633eb0a8d1b_l3.png)
Pattern w.r.t n is seen here, as follows
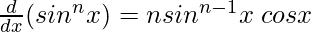
Let’s check this statement.
For 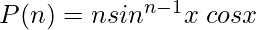
For P(1),
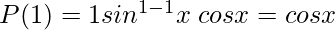 . Which is true.
. Which is true.
n=k
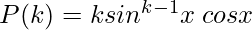
n = k+1
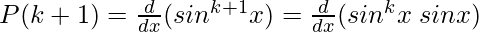
Using the product rule, we have
(uv)’ = uv’+vu’
![Rendered by QuickLaTeX.com = (sin^k x) \frac{d}{dx}(sin x) + (sin x) \frac{d}{dx}(sin^k x)\\ = (sin^k x) (cos x) + (sin x) (k sin^{k-1}x \hspace{0.1cm}cos x)\\ = (sin^k x) (cos x)[k+1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2cd8f985d319e1a753c26b6e23b1d92e_l3.png)
Hence proved for P(k+1).
So, 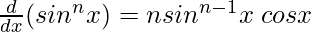 is true.
is true.
So, the given equation will be
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...