Class 11 NCERT Solutions – Chapter 13 Limits And Derivatives – Exercise 13.2
Last Updated :
30 Aug, 2022
Question 1. Find the derivative of x2 – 2 at x = 10.
Solution:
f(x) = x2 – 2
f(x+h) = (x+h)2 – 2
From the first principle,
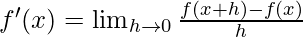
When, x = 10
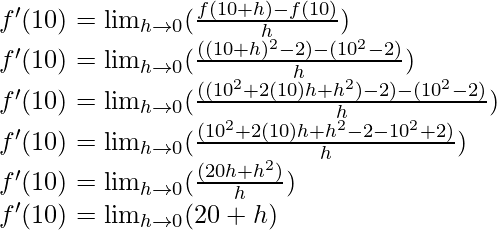
f'(10) = 20 + 0
f'(10) = 20
Question 2. Find the derivative of x at x = 1.
Solution:
f(x) = x
f(x+h) = x+h
From the first principle,
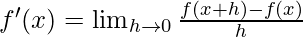
When, x = 1
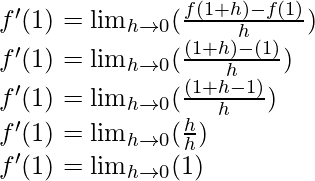
f'(1) = 1
Question 3. Find the derivative of 99x at x = l00.
Solution:
f(x) = 99x
f(x+h) = 99(x+h)
From the first principle,
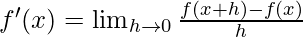
When, x = 10
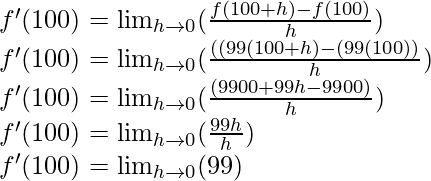
f'(100) = 99
Question 4. Find the derivative of the following functions from first principle.
(i) x3 − 27
Solution:
f(x) = x3 – 27
f(x+h) = (x+h)3 – 27
From the first principle,
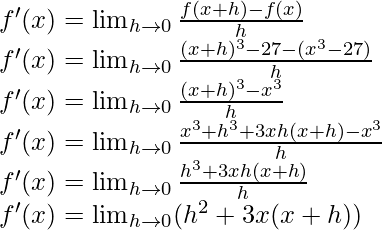
f'(x) = 02+3x(x+0)
f'(x) = 3x2
(ii) (x-1) (x-2)
Solution:
f(x) = (x-1) (x-2) = x2 – 3x + 2
f(x) = (x+h)2 – 3(x+h) + 2
From the first principle,
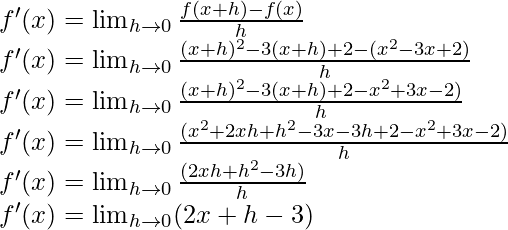
f'(x) = 2x+0 – 3
f'(x) = 2x – 3
(iii) 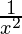
Solution:
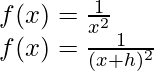
From the first principle,
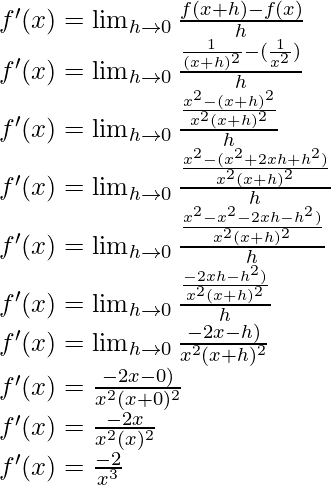
(iv) 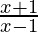
Solution:
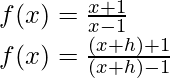
From the first principle,
![Rendered by QuickLaTeX.com f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x+h)+1}{(x+h)-1}-(\frac{x+1}{x-1})}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x+h+1)(x-1)-(x+h-1)(x+1)}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x^2+hx+x)-(x+h+1)-[(x^2+hx-x)+(x+h-1)]}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x^2+hx+x-x-h-1)-(x^2+hx-x+x+h-1)}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x^2+hx+x-x-h-1-x^2-hx+x-x-h+1)}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(-h-h)}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{-2h}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{-2h}{h(x+h-1)(x-1)}\\ f'(x) = \lim_{h \to 0} \frac{-2}{(x+h-1)(x-1)}\\ f'(x) = \frac{-2}{(x-1)(x-1)}\\ f'(x) = \frac{-2}{(x-1)^2}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91b8d72ab017d6d69ca4c37756b5418a_l3.png)
Question 5. For the function
f(x) = 
Prove that f'(1) = 100 f'(0)
Solution:
Given,
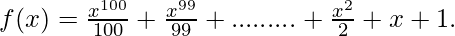
By using this, taking derivative both sides
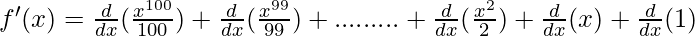
As, the derivative of xn is nxn-1 and derivative of constant is 0.
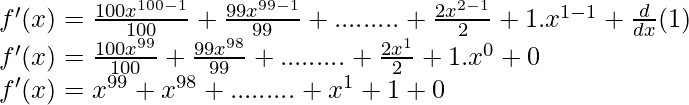
Now, then

Hence, we conclude that
f'(1) = 100 f'(0)
Question 6. Find the derivative of xn + axn-1 + a2xn-2 + ……………….+ an-1x + an for some fixed real number a.
Solution:
Given,
f(x) = xn + axn-1 + a2xn-2 + ……………….+ an-1x + an
As, the derivative of xn is nxn-1 and derivative of constant is 0.
By using this, taking derivative both sides
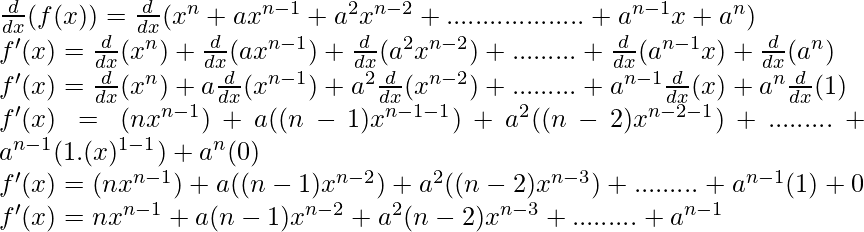
Question 7. For some constants a and b, find the derivative of
(i) (x-a) (x-b)
Solution:
f(x) = (x-a) (x-b)
f(x) = x2 – (a+b)x + ab
Taking derivative both sides,
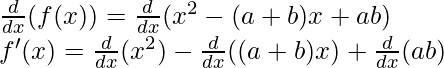
As, the derivative of xn is nxn-1 and derivative of constant is 0.
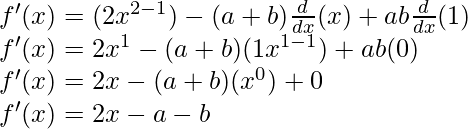
(ii) (ax2 + b)2
Solution:
f(x) = (ax2 + b)2
f(x) = (ax2)2 + 2(ax2)(b) + b2
Taking derivative both sides,
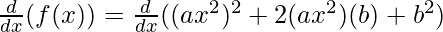
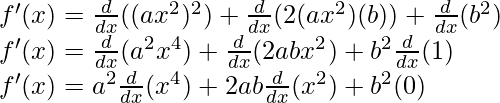
As, the derivative of xn is nxn-1 and derivative of constant is 0.
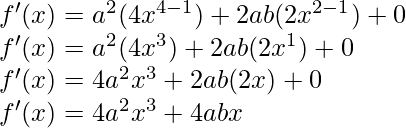
(iii) 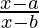
Solution:
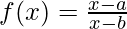
Taking derivative both sides,
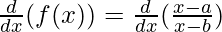
Using quotient rule, we have
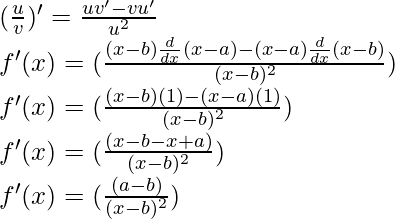
Question 8. Find the derivative of 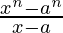 for some constant a.
for some constant a.
Solution:
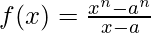
Taking derivative both sides,
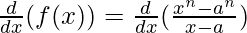
Using quotient rule, we have
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-vu'}{u^2}\\ f'(x) = (\frac{(x-a)\frac{d}{dx}(x^n-a^n)-(x^n-a^n)\frac{d}{dx}(x-a)}{(x-a)^2})\\ f'(x) = (\frac{(x-a)[\frac{d}{dx}(x^n)-\frac{d}{dx}(a^n)]-(x^n-a^n)(1)}{(x-a)^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1fabc7085a2485c7752ea1eb118d5ecc_l3.png)
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = (\frac{(x-a)[(nx^{n-1})-0)]-(x^n-a^n)}{(x-a)^2})\\ f'(x) = (\frac{(x-a)(nx^{n-1})-x^n+a^n}{(x-a)^2})\\ f'(x) = (\frac{(nx^{n-1+1}-anx^{n-1})-x^n+a^n}{(x-a)^2})\\ f'(x) = (\frac{(nx^n-anx^{n-1})-x^n+a^n}{(x-a)^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc673e844e4e02a28ffd81bede0e7dfe_l3.png)
Question 9. Find the derivative of
(i) 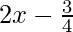
Solution:
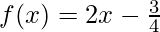
Taking derivative both sides,
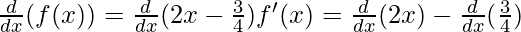
As, the derivative of xn is nxn-1 and derivative of constant is 0.
f'(x) = (2x0)-0
f'(x) = 2
(ii) (5x3 + 3x – 1)(x-1)
Solution:
f(x) = (5x3 + 3x – 1)(x-1)
Taking derivative both sides,
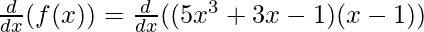
Using product rule, we have
(uv)’ = uv’ + u’v
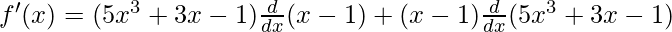
As, the derivative of xn is nxn-1 and derivative of constant is 0.
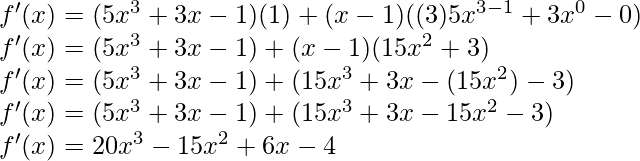
(iii) x-3 (5+3x)
Solution:
f(x) = x-3 (5+3x)
Taking derivative both sides,
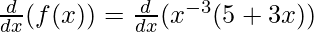
Using product rule, we have
(uv)’ = uv’ + u’v
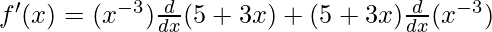
As, the derivative of xn is nxn-1 and derivative of constant is 0.
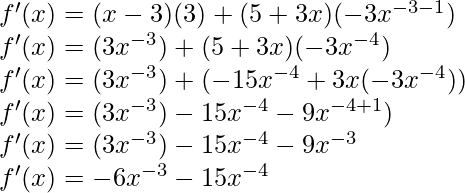
(iv) x5 (3-6x-9)
Solution:
f(x) = x5 (3-6x-9)
Taking derivative both sides,
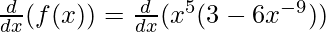
Using product rule, we have
(uv)’ = uv’ + u’v
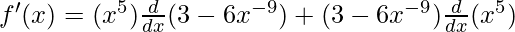
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = (x^5)[\frac{d}{dx}(3)-\frac{d}{dx}(6x^{-9})] + (3-6x^{-9})(5x^{5-1})\\ f'(x) = (x^5)[0-((-9)6x^{-9-1})] + (3-6x^{-9})(5x^{4})\\ f'(x) = (x^5)(54x^{-10}) + (3(5x^{4})-6x^{-9}(5x^{4}))\\ f'(x) = 54x^{-10+5} + (15x^{4} -30x^{-9+4})\\ f'(x) = 54x^{-5} + 15x^{4} -30x^{-5}\\ f'(x) = 24x^{-5} + 15x^{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-77656a874a44bca53ca9f3306eda1850_l3.png)
(v) x-4 (3-4x-5)
Solution:
f(x) = x-4 (3-4x-5)
Taking derivative both sides,
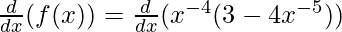
Using product rule, we have
(uv)’ = uv’ + u’v
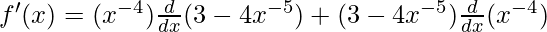
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = (x^{-4})[\frac{d}{dx}(3)-\frac{d}{dx}(4x^{-5})] + (3-4x^{-5})(-4x^{-4-1})\\ f'(x) = (x^{-4})[0-(4(-5)x^{-5-1})] + (3-4x^{-5})(-4x^{-5})\\ f'(x) = (x^{-4})[20x^{-6})] + (3(-4x^{-5})-4x^{-5}(-4x^{-5}))\\ f'(x) = (20x^{-6-4}) + (-12x^{-5}-16x^{-5-5})\\ f'(x) = (20x^{-10}) - 12x^{-3} - 16x^{-12})\\ f'(x) = 36x^{-10} - 12x^{-3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec4fcdd0d98dbeb73cef749247bad43d_l3.png)
(vi) 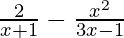
Solution:
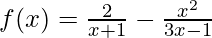
Taking derivative both sides,
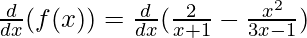
Using quotient rule, we have
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-vu'}{u^2}\\ f'(x) = [\frac{(x+1)\frac{d}{dx}(2)-(2)\frac{d}{dx}(x+1)}{(x+1)^2})] - [\frac{(3x-1)\frac{d}{dx}(x^2)-(x^2)\frac{d}{dx}(3x-1)}{(3x-1)^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eb89f4177412181a6dfaa7ede178c05e_l3.png)
As, the derivative of xn is nxn-1 and derivative of constant is 0.
![Rendered by QuickLaTeX.com f'(x) = [\frac{(x+1)(0)-(2)(1)}{(x+1)^2})] - [\frac{(3x-1)(2x^{2-1})-(x^2)(3)}{(3x-1)^2})]\\ f'(x) = [\frac{-2}{(x+1)^2})] - [\frac{(3x-1)(2x)-(x^2)(3)}{(3x-1)^2})]\\ f'(x) = [\frac{-2}{(x+1)^2})] - [\frac{(6x^2-2x)-3x^2)}{(3x-1)^2})]\\ f'(x) = \frac{-2}{(x+1)^2}) - \frac{(3x^2-2x)}{(3x-1)^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-981d515c7ef36490f7b0265778a666cb_l3.png)
Question 10. Find the derivative of cos x from first principle.
Solution:
Here, f(x) = cos x
f(x+h) = cos (x+h)
From the first principle,
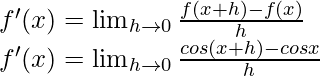
Using the trigonometric identity,
cos a – cos b = -2 sin 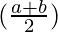 sin
sin 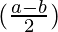
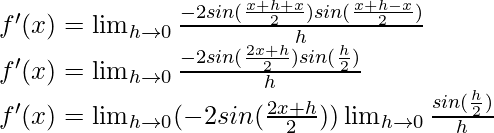
Multiplying and dividing by 2,
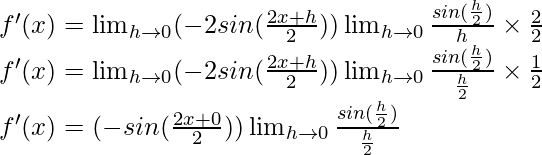
f'(x) = -sin (x) (1)
f'(x) = -sin x
Question 11. Find the derivative of the following functions:
(i) sin x cos x
Solution:
f(x) = sin x cos x
f(x+h) = sin (x+h) cos (x+h)
From the first principle,
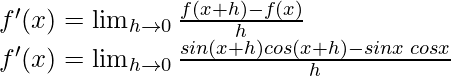
Using the trigonometric identity,
sin A cos B = 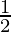 (sin (A+B) + sin(A-B))
(sin (A+B) + sin(A-B))
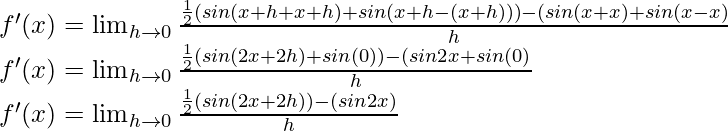
Using the trigonometric identity,
sin A – sin B = 2 cos 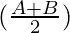 sin
sin 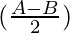
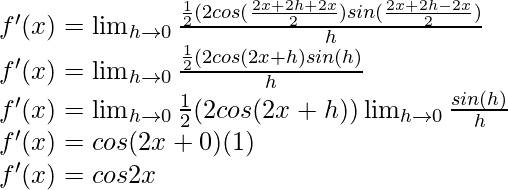
(ii) sec x
Solution:
f(x) = sec x = 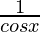
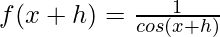
From the first principle,
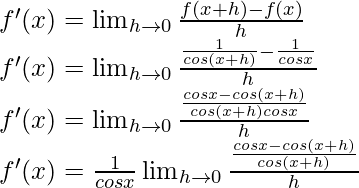
Using the trigonometric identity,
cos a – cos b = -2 sin 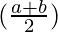 sin
sin 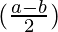
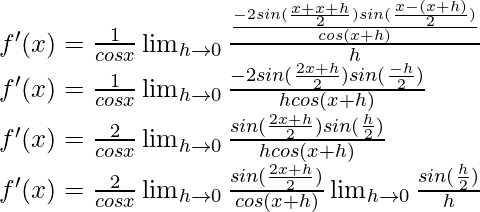
Multiply and divide by 2, we have
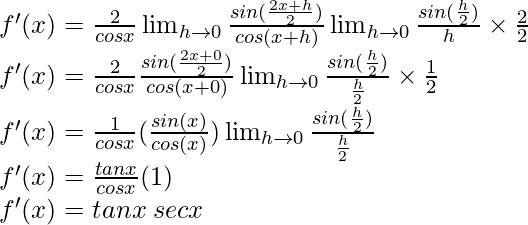
(iii) 5 sec x + 4 cos x
Solution:
f(x) = 5 sec x + 4 cos x
Taking derivative both sides,
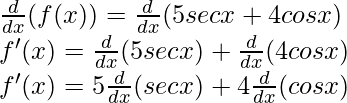
f'(x) = 5 (tan x sec x) + 4 (-sin x)
f'(x) = 5 tan x sec x – 4 sin x
(iv) cosec x
Solution:
f(x) = cosec x = 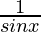
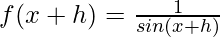
From the first principle,
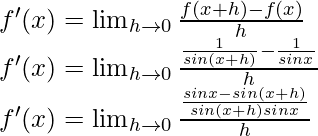
Using the trigonometric identity,
sin a – sin b = 2 cos 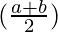 sin
sin 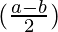
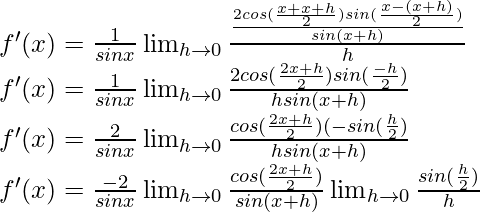
Multiply and divide by 2, we have
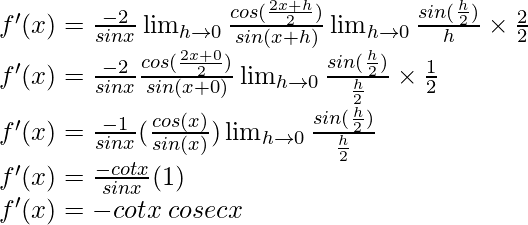
(v) 3 cot x + 5 cosec x
Solution:
f(x) = 3 cot x + 5 cosec x
Taking derivative both sides,
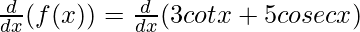
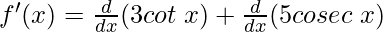
f'(x) = 3 g'(x) + 5 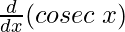
Here,
g(x) = cot x = 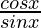
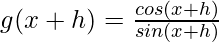
From the first principle,
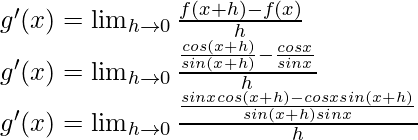
Using the trigonometric identity,
sin a cos b – cos a sin b = sin (a-b)
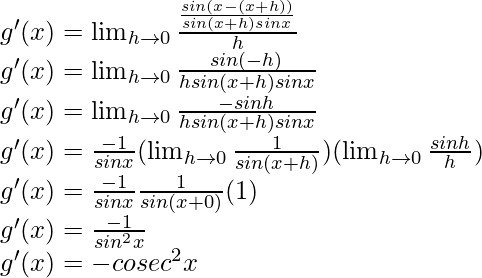
So, now
f'(x) = 3 g'(x) + 5 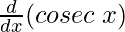
f'(x) = 3 (- cosec2 x) + 5 (-cot x cosec x)
f'(x) = – 3cosec2 x – 5 cot x cosec x
(vi) 5 sin x – 6 cos x + 7
Solution:
f(x) = 5 sin x – 6 cos x + 7
f(x+h) = 5 sin (x+h) – 6 cos (x+h) + 7
From the first principle,
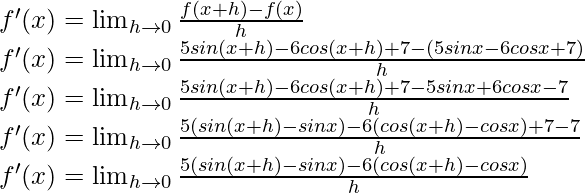
Using the trigonometric identity,
sin a – sin b = 2 cos 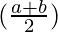 sin
sin 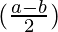
cos a – cos b = -2 sin 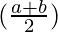 sin
sin 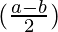
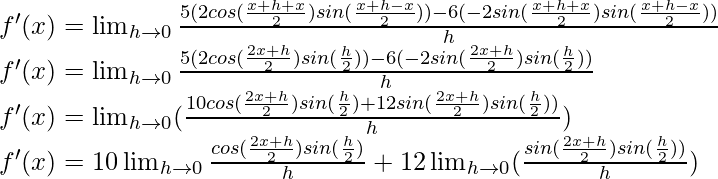
Multiply and divide by 2, we get
![Rendered by QuickLaTeX.com f'(x) = \frac{2}{2}[10 \lim_{h \to 0} \frac{cos (\frac{2x+h}{2}) sin (\frac{h}{2})}{h} + 12 \lim_{h \to 0} (\frac{sin (\frac{2x+h}{2}) sin (\frac{h}{2}))}{h})]\\ f'(x) = \frac{1}{2}[10 \lim_{h \to 0} \frac{cos (\frac{2x+h}{2}) sin (\frac{h}{2})}{\frac{h}{2}} + 12 \lim_{h \to 0} (\frac{sin (\frac{2x+h}{2}) sin (\frac{h}{2}))}{\frac{h}{2}})]\\ f'(x) = 5 cos (\frac{2x+0}{2}) \lim_{h \to 0}\frac{ sin (\frac{h}{2})}{\frac{h}{2}} + 6 (sin (\frac{2x+0}{2}) \lim_{h \to 0} \frac{sin (\frac{h}{2}))}{\frac{h}{2}})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8f6f84674f37c703aeee780f044499a4_l3.png)
f'(x) = 5 cos x (1) + 6 sin x (1)
f'(x) = 5 cos x + 6 sin x
(vii) 2 tan x – 7 sec x
Solution:
f(x) = 2 tan x – 7 sec x
Taking derivative both sides,
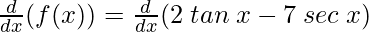
f'(x) = 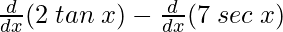
f'(x) = 2 g'(x) – 7 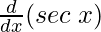
Here,
g(x) = tan x = 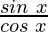
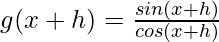
From the first principle,
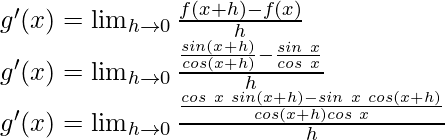
Using the trigonometric identity,
sin a cos b – cos a sin b = sin (a-b)
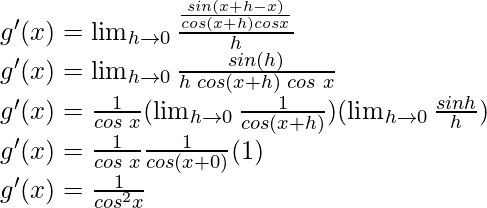
g'(x) = sec2x
So, now
f'(x) = 2 g'(x) – 7 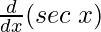
f'(x) = 2 (sec2x) – 7 (sec x tan x)
f'(x) = 2sec2x – 7 sec x tan x
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...