Class 11 NCERT Solutions- Chapter 13 Limits And Derivatives – Exercise 13.1 | Set 2
Last Updated :
07 Apr, 2021
Question 17: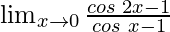
Solution:
In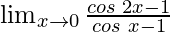 , as x⇢0
, as x⇢0
As we know, cos 2θ = 1-2sin2θ
Substituting the values, we get
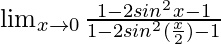
=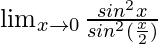
Put x = 0, we get
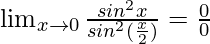
As, this limit becomes undefined
Now, let’s multiply and divide the numerator by x2 and denominator by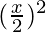 to make it equivalent to theorem.
to make it equivalent to theorem.
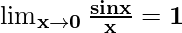
Hence, we have
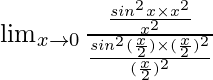
=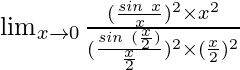
=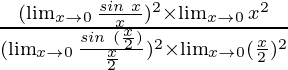
By using the theorem, we get
=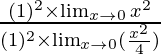
=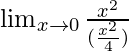
=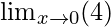
= 4
Question 18: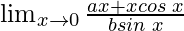
Solution:
In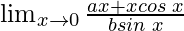 , as x⇢0
, as x⇢0
Put x = 0, we get
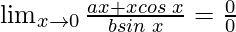
As, this limit becomes undefined
Now, let’s simplify the equation to make it equivalent to theorem.
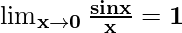
Hence, we have
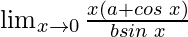
=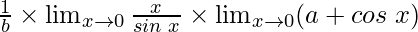
By using the theorem, we get
=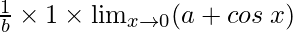
=
Putting x=0, we have
=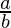
Question 19: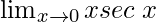
Solution:
In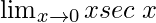 , as x⇢0
, as x⇢0
Put x = 0, we get
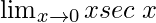 = 0 ×1
= 0 ×1
= 0
Question 20: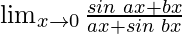
Solution:
In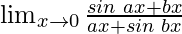 , as x⇢0
, as x⇢0
Put x = 0, we get
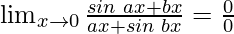
As, this limit becomes undefined
Now, let’s simplify the equation to make it equivalent to theorem.
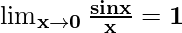
Hence, we can write the equation as follows:
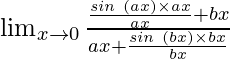
=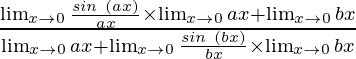
By using the theorem, we get
=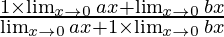
=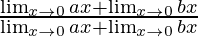
=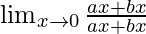
=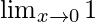
Putting x=0, we have
= 1
Question 21: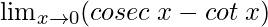
Solution:
In , as x⇢0
, as x⇢0
By simplification, we get
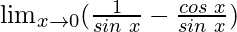
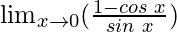
Put x = 0, we get
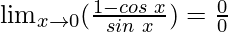
As, this limit becomes undefined
Now, let’s simplify the equation to make it equivalent to theorem:
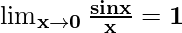
By using the trigonometric identities,
cos 2θ = 1-2sin2θ
sin 2θ = 2 sinθ cosθ
Hence, we can write the equation as follows:
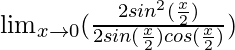
=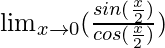
=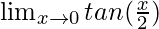
Putting x=0, we have
= 0
Question 22: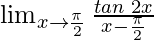
Solution:
In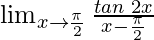 , as x⇢
, as x⇢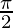
Put x =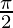 , we get
, we get
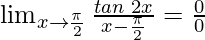
As, this limit becomes undefined
Now, let’s simplify the equation :
Let’s take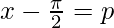
As, x⇢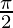 ⇒ p⇢0
⇒ p⇢0
Hence, we can write the equation as follows:
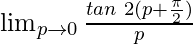
=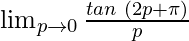
=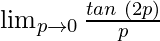 (As tan (π+θ) = tan θ)
(As tan (π+θ) = tan θ)
=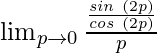
=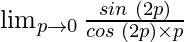
Now, let’s multiply and divide the equation by 2 to make it equivalent to theorem
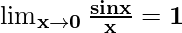
=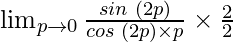
=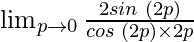
As p⇢0, then 2p⇢0
=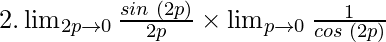
Using the theorem and putting p=0, we have
= 2×1×1
= 2
Question 23: Find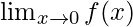 and
and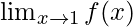 , where
, where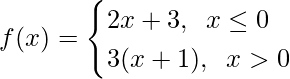
Solution:
Let’s calculate, the limits when x⇢0
Here,
Left limit =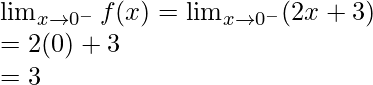
Right limit =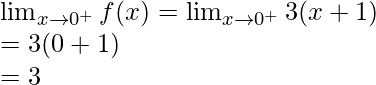
Limit value =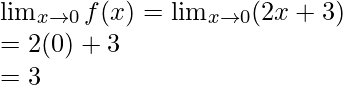
Hence,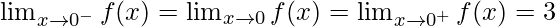 , then limit exists
, then limit exists
Now, let’s calculate, the limits when x⇢1
Here,
Left limit =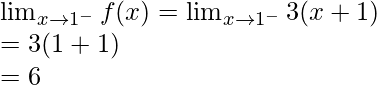
Right limit =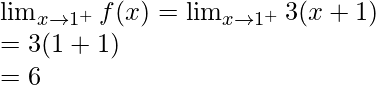
Limit value =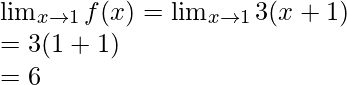
Hence,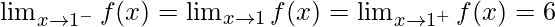 , then limit exists
, then limit exists
Question 24: Find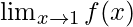 , where
, where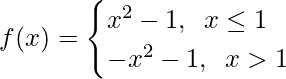
Solution:
Let’s calculate, the limits when x⇢1
Here,
Left limit =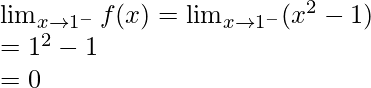
Right limit =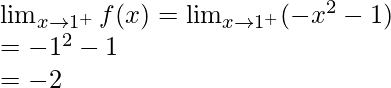
As,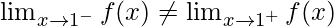
Hence, limit does not exists when x⇢1.
Question 25: Evaluate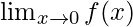 , where
, where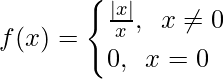
Solution:
Let’s calculate, the limits when x⇢0
Here,
As, we know that mod function works differently.
In |x-0|, |x|=x when x>0 and |x|=-x when x<0
Left limit =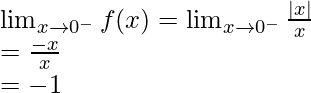
Right limit =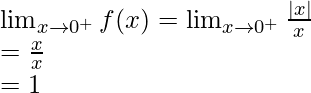
As,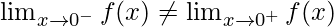
Hence, limit does not exists when x⇢0.
Question 26: Find 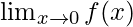 , where
, where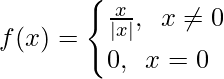
Solution:
Let’s calculate, the limits when x⇢0
Here,
As, we know that mod function works differently.
In |x-0|, |x|=x when x>0 and |x|=-x when x<0
Left limit =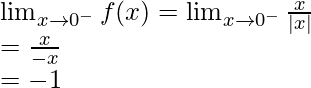
Right limit =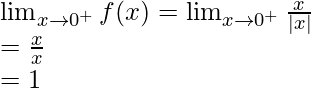
As,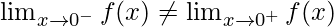
Hence, limit does not exists when x⇢0.
Question 27: Find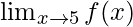 , where f(x)=|x|-5.
, where f(x)=|x|-5.
Solution:
Let’s calculate, the limits when x⇢5
Here,
As, we know that mod function works differently.
In |x-0|, |x|=x when x>0 and |x|=-x when x<0
Left limit =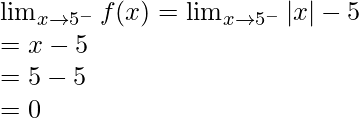
Right limit =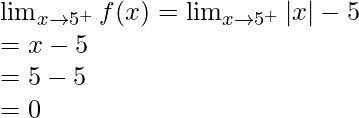
Hence,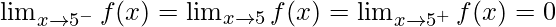 , then limit exists
, then limit exists
Question 28: Suppose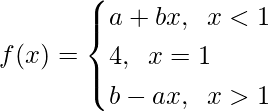 and if
and if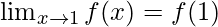 what are possible values of a and b?
what are possible values of a and b?
Solution:
As, it is given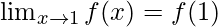
Let’s calculate, the limits when x⇢1
Here,
Left limit =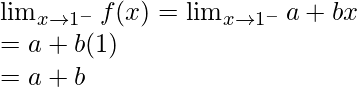
Right limit =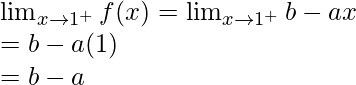
Limit value f(1) = 4
So, as limit exists then it should satisfy
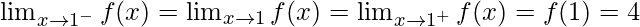
Hence, a+b = 4 and b-a = 4
Solving these equation, we get
a = 0 and b = 4
Question 29: Let a1, a2, . . ., an be fixed real numbers and define a function
f(x) = (x-a1) (x-a2)………… (x-an).
What is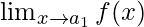 ? For some a ≠ a1, a2, …, an, compute
? For some a ≠ a1, a2, …, an, compute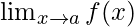 .
.
Solution:
Here, f(x) = (x-a1) (x-a2)………… (x-an).
Then,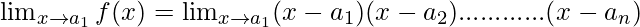
=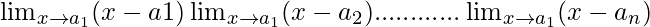
= (a1-a1) (a1-a2)………… (a1-an)
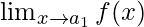 = 0
= 0
Now, let’s calculate for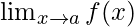
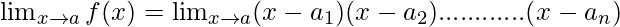
=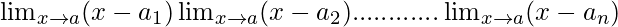
= (a-a1) (a-a2)………… (a-an)
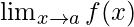 = (a-a1) (a-a2)………… (a-an)
= (a-a1) (a-a2)………… (a-an)
Question 30: If
For what value (s) of a does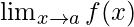 exists?
exists?
Solution:
Here,
As, we know that mod function works differently.
In |x-0|, |x|=x when x>0 and |x|=-x when x<0
Let’s check for three cases of a:
Let’s calculate, the limits when x⇢0
Left limit =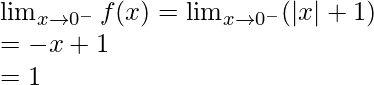
Right limit =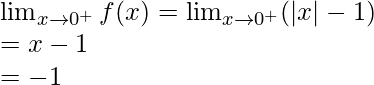
As,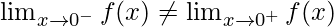
Hence, limit does not exists when x⇢0.
Let’s take a=2, for reference
Let’s calculate, the limits when x⇢2
Left limit =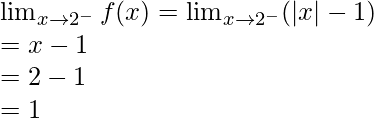
Right limit =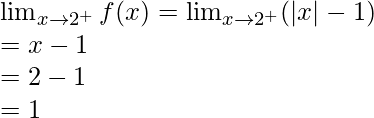
As,
Hence, limit exists when x⇢2.
Let’s take a=-2, for reference
Let’s calculate, the limits when x⇢ -2
Left limit =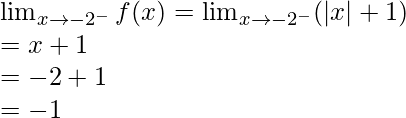
Right limit =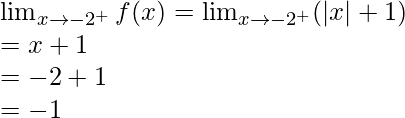
As,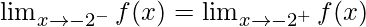
Hence, limit exists when x⇢ -2.
Question 31: If the function f(x) satisfies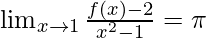 , evaluate
, evaluate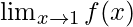
Solution:
Here, as it is given
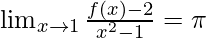
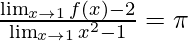
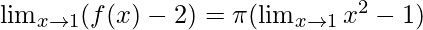
Put x = 1 in RHS, we get
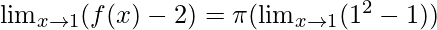
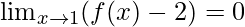
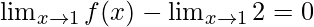
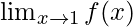 = 2
= 2
Hence proved!
Question 32: If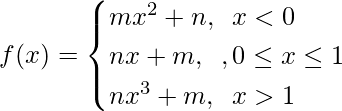 . For what integers m and n does both
. For what integers m and n does both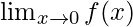 and
and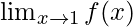 exists?
exists?
Solution:
Let’s calculate, the limits when x⇢0
Here,
Left limit =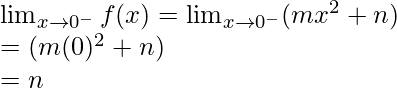
Right limit =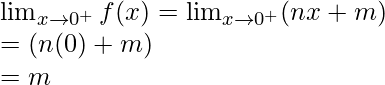
Hence,
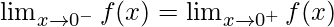 , then limit exists
, then limit exists
m = n
Now, let’s calculate, the limits when x⇢1
Here,
Left limit =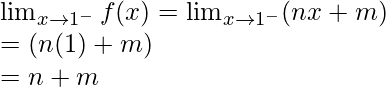
Right limit =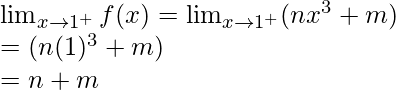
Hence,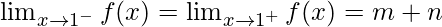 , then limit exists.
, then limit exists.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...