Class 11 NCERT Solutions- Chapter 12 Introduction to three dimensional Geometry – Exercise 12.3
Last Updated :
09 Mar, 2021
Problem 1: Find the coordinates of the point which divides the line segment joining the points (– 2, 3, 5) and (1, – 4, 6) in the ratio.
(i) 2: 3 internally
Solution:
By using Section formula,
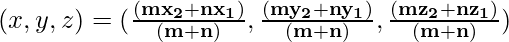
Upon comparing we get,
x1 = -2, y1 = 3, z1 = 5
x2 = 1, y2 = -4, z2 = 6 and
m = 2, n = 3
So, the coordinates of the point which divides the line segment joining the points P (– 2, 3, 5) and Q (1, – 4, 6) in the ratio 2 : 3 internally is given by:
((2 * 1 + 3 * -2)/(2 + 3), (2 * -4 + 3 * 3)/(2 + 3), (2 * 6 + 3 * 5)/(2 + 3))
((-4/5), (1/5), (27/5))
Hence, the coordinates of the point which divides the line segment joining the points (-2, 3, 5) and (1, -4, 6) is (-4/5, 1/5, 27/5)
(ii) 2: 3 externally
Solution:
By using Section formula,
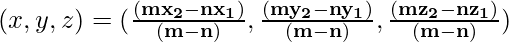
Upon comparing we get,
x1 = -2, y1 = 3, z1 = 5;
x2 = 1, y2 = -4, z2 = 6 and
m = 2, n = 3
So, the coordinates of the point which divides the line segment joining the points P (– 2, 3, 5) and Q (1, – 4, 6) in the ratio 2: 3 externally is given by:
((2 * 1 – 3 * -2)/(2 + 3), (2 * -4 – 3 * 3)/(2 + 3), (2 * 6 – 3 * 5)/(2 + 3))
((2 + 6)/(-1), (-8 – 9)/(-1), (12 – 15)/(-1)
(-8), (17), (3)
∴ The co-ordinates of the point which divides the line segment joining the points (-2, 3, 5) and (1, -4, 6) is (-8, 17, 3).
Problem 2: Given that P (3, 2, – 4), Q (5, 4, – 6) and R (9, 8, –10) are collinear. Find the ratio in which Q divides PR.
Solution:
Let us consider Q divides PR in the ratio k: 1.
By using Section formula,
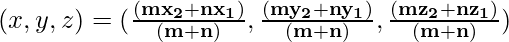
Upon comparing we get,
x1 = 3, y1 = 2, z1 = -4;
x2 = 9, y2 = 8, z2 = -10 and
m = k, n = 1
So, we have
((k * 9 + 1 * 3)/(k + 1), (k * 8 + 1 * 2)/(k + 1), (-10 * k + 1 * -4)/(k + 1) = (5, 4, -6)
(9k + 3)/(k + 1) = 5, (8k + 2)/(k + 1) = 4, (-10k + -4)/(k + 1) = -6
(8k + 2)/(k + 1) = 4
8k + 2 = 4k + 4
4k = 2
k = 1/2
Hence, the ratio in which Q divides PR is 1: 2
Problem 3: Find the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8).
Solution:
Let the line segment formed by joining the points P (-2, 4, 7) and Q (3, -5, 8) be PQ.
We know that any point on the YZ-plane is of the form (0, y, z).
So now, let R (0, y, z) divides the line segment PQ in the ratio k: 1.
Then,
Upon comparing we get,
x1 = -2, y1 = 4, z1 = 7;
x2 = 3, y2 = -5, z2 = 8 and
m = k, n = 1
By using the Section formula,
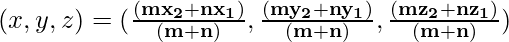
So we have,
((3k – 2)/(k + 1), (-5k + 4)/(k + 1), (8k + 7)/(k + 1)) = (0, y, z)
3k – 2 = 0
3k = 2
k = 2/3
Hence, the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8) is 2:3.
Problem 4: Using section formula, show that the points A (2, –3, 4), B (–1, 2, 1) and C (0, 1/3, 2) are collinear.
Solution:
Let the point P divides AB in the ratio k: 1.
Upon comparing we get,
x1 = 2, y1 = -3, z1 = 4;
x2 = -1, y2 = 2, z2 = 1 and
m = k, n = 1
By using Section formula,
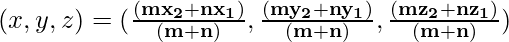
So we have,
The coordinates of P are:
((-k + 2)/(k + 1), (2k – 3)/(k + 1), (k + 4)/(k + 1))
Now, we check if for some value of k, the point coincides with the point C.
Put (-k + 2)/(k + 1) = 0
-k + 2 = 0
k = 2
When k = 2, then (2k – 3)/(k + 1) = (2(2) – 3)/(2 + 1)
= (4 – 3)/3
= 1/3
And, (k + 4)/(k +1) = (2 + 4)/(2 +1)
= 6/3
= 2
∴ C (0, 1/3, 2) is a point which divides AB in the ratio 2: 1 and is same as P.
Hence, A, B, C are collinear.
Problem 5: Find the coordinates of the points which trisect the line segment joining the points P (4, 2, – 6) and Q (10, –16, 6).
Solution:
Let A (x1, y1, z1) and B (x2, y2, z2) trisect the line segment joining the points P (4, 2, -6) and Q (10, -16, 6).
A divides the line segment PQ in the ratio 1: 2.
Upon comparing we get,
x1 = 4, y1 = 2, z1 = -6;
x2 = 10, y2 = -16, z2 = 6 and
m = 1, n = 2
By using the Section formula,
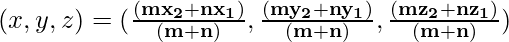
So we have,
The coordinates of A are:
((1*10 + 2*4)/(1 + 2), (1*(-16) + 2*2)/(1 + 2), (1*6 + 2*(-6))/(1 + 2)
((18/3), (-12/3), (-6/3))
The coordinates of A are (6, -4, -2)
Similarly, we know that B divides the line segment PQ in the ratio 2: 1.
Upon comparing we get,
x1 = 4, y1 = 2, z1 = -6;
x2 = 10, y2 = -16, z2 = 6 and
m = 2, n = 1
By using the Section formula,
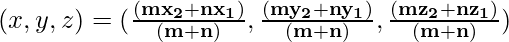
So we have,
The coordinates of B are:
((2 * 10 + 1 * 4)/(2 + 1), (2 * -16 + 1 * 2)/(2 + 1), (2 * 6 + 1 * -6)/(2 + 1)
The coordinates of B are (8, -10, 2)
∴ The coordinates of the points which trisect the line segment joining the points P (4, 2, – 6) and Q (10, –16, 6) are (6, -4, -2) and (8, -10, 2).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...