Question 13. Show that the equation of the line passing through the origin and making an angle θ with the line y = mx + c is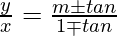 .
.
Solution:
Suppose y = m1x is the equation of the line passing through the origin. Hence, slope of this line is,
m1 =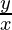
Given line is y = mx + c whose slope is m. It makes an angle θ with the line y = m1x.
=> tan θ =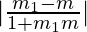
=> = tan θ
= tan θ
=>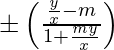 = tan θ
= tan θ
=>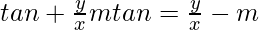 or
or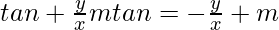
=>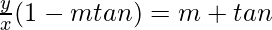 or
or
=>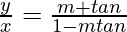 or
or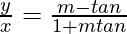
=>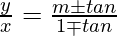
Hence proved.
Question 14. In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4?
Solution:
We know that the equation of the line joining (–1, 1) and (5, 7) is given by,
=> y – 1 =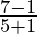 (x + 1)
(x + 1)
=> y – 1 = x + 1
=> x – y + 2 = 0 . . . . (1)
We are given the line, x + y = 4 . . . . (2)
Solving (1) and (2), we get the point of intersection of these lines,
x = 1 and y = 3
Suppose the point (1, 3) divides the line joining (–1, 1) and (5, 7) in the ratio 1 : k.
Using section formula, we get,
(1, 3) =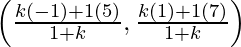
(1, 3) =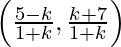
We get,
=> – k + 5 = 1 + k
=> 2k = 4
=> k = 2
Therefore, the line joining the points (–1, 1) and (5, 7) is divided by the line x + y = 4 in the ratio 1 : 2.
Question 15. Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.
Solution:
We are given,
2x – y = 0 . . . . (1)
4x + 7y + 5 = 0 . . . . (2)
Solving (1) and (2), we get the point of intersection of lines,
x = –5/18 and y = –5/9.

So, we get B (–5/18, –5/9) and we have A (1, 2). Now we have to find the distance AB.
Using the distance formula, we get,
AB =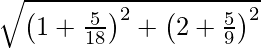
=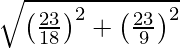
=
=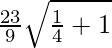
=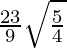
=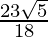 units
units
Therefore, the required distance is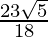 units.
units.
Question 16. Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.
Solution:
Suppose y = mx + c is the line passing through the point (–1, 2). So we get
=> 2 = m (–1) + c
=> 2 = –m + c
=> c = m + 2
Putting the value of c in the equation, we get,
y = mx + m + 2 . . . . (1)
Now the given line is
x + y = 4 . . . . (2)
By solving both the equations we get the point of intersection of these lines,
x =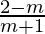 , y =
, y =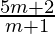
Now the point is at a distance of 3 units from the point (–1, 2).
is at a distance of 3 units from the point (–1, 2).
From distance formula, we get,
=>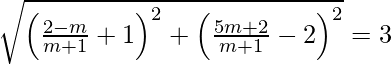
=>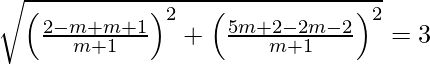
=>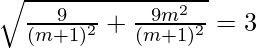
=>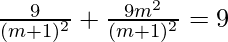
=>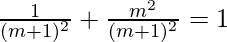
=>
=> 1 + m2 = m2 + 1 + 2m
=> 2m = 0
=> m = 0
As the slope of the required line is zero, the line must be parallel to the x-axis.
Question 17. The hypotenuse of a right-angled triangle has its ends at the points (1, 3) and (−4, 1). Find the equation of the legs (perpendicular sides) of the triangle.
Solution:
Suppose △ABC is right-angled triangle where ∠ C = 90o and m is the slope of AC.
So the slope of BC = –1/m. And the equation of AC is given by,
=> y – 3 = m (x – 1)
=> x – 1 = 1/m (y – 3)
We know the equation of BC is given by,
=> y – 1 = – 1/m (x + 4)
=> x + 4 = – m (y – 1)
If m = 0, we get the equations of perpendicular sides,
y – 3 = 0 and x + 4 = 0 or,
y = 3 and x = –4
If m = ∞, we get the equations,
x – 1 = 0 and y – 1 = 0 or,
x = 1 and y = 1
Question 18. Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Solution:
We are given that
x + 3y = 7 . . . . (1)
Suppose B (a, b) is the image of point A (3, 8). Hence line (1) is the perpendicular bisector of AB.

Slope of line (1) = −1/3
And slope of line AB =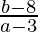
We know, AB and line (1) are perpendicular, so we have,
=>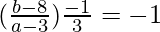
=>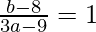
=> 3a − b = 1 . . . . (2)
Now, mid-point of AB =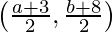 . As the mid-point is satisfying line (1), we get,
. As the mid-point is satisfying line (1), we get,
=>
=> a + 3 + 3b + 24 = 14
=> a + 3b = −13 . . . . (3)
Solving (2) and (3), we get, a = –1 and b = –4
Therefore, the image of the given point with respect to the given line is (–1, –4).
Question 19. If the lines y = 3x + 1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.
Solution:
We are given,
y = 3x + 1 . . . . (1)
2y = x + 3 . . . . (2)
y = mx + 4 . . . . (3)
So the slope of line (1), a = 3,
line (2), b = 1/2
line (3), c = m
It is given that the lines (1) and (2) are equally inclined to line (3) which implies that the angle between lines (1) and (3) equals the angle between lines (2) and (3).
=>
=>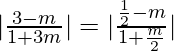
=>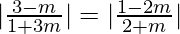
=>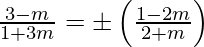
=>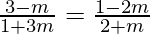 or
or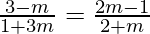
=>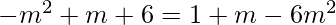 or
or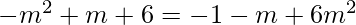
=> 5m2 + 5 = 0 (ignored) or 7m2 − 2m − 7 = 0
=> 7m2 − 2m − 7 = 0
=> m =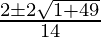
=> m =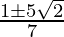
Hence the required value of m is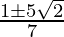 .
.
Question 20. If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y + 7 = 0 is always 10. Show that P must move on a line.
Solution:
We are given lines,
x + y – 5 = 0 . . . . (1)
3x – 2y + 7 = 0 . . . . (2)
Now, we know that the perpendicular distance(d) of a line Ax + By + C = 0 from (x, y) is given by,
d =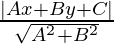
So, perpendicular distance(d1) of a line x + y – 5 = 0 from (x, y) is,
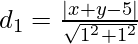
=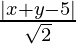
And the perpendicular distance(d2) of a line 3x – 2y + 7 = 0 from (x, y) is,
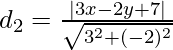
=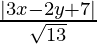
According to the question,
=> d1 + d2 = 10
=>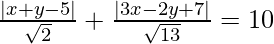
=>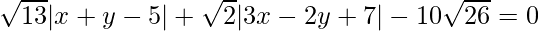
=>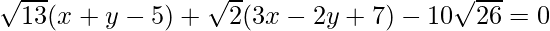
=>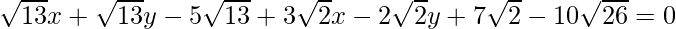
=>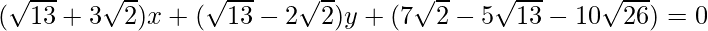
As the equation represents a line, P must move on a line.
Hence, proved.
Question 21. Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
Solution:
We are the given the lines,
9x + 6y – 7 = 0 . . . . (1)
3x + 2y + 6 = 0 . . . . (2)
Let (a, b) be the point lying on the line which is equidistant from (1) and (2).
Now, we know that the perpendicular distance(d) of a line Ax + By + C = 0 from (x, y) is given by,
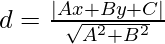
So, perpendicular distance(d1) of a line 9x + 6y – 7 = 0 from (a, b) is,
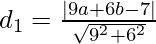
=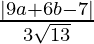
And the perpendicular distance(d2) of a line 3x + 2y + 6 = 0 from (a, b) is,
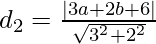
=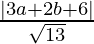
According to the question,
=> d1 = d2
=>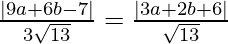
=> |9a + 6b − 7| = 3 |3a + 2b + 6|
=> 9h + 6k – 7 = 3 (3h + 2k + 6) or 9h + 6k – 7 = – 3 (3h + 2k + 6)
=> 9h + 6k – 7 = 9h + 6k + 18 or 9h + 6k – 7 = –9h – 6k – 18
=> – 7 = 18 (ignored) or 18h + 12k + 11 = 0
=> 18h + 12k + 11 = 0
Therefore, the required equation of the line is 18x + 12y + 11 = 0.
Question 22. A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
Solution:

The perpendicular line from the axes divides the ∠ BAC = 90o in two equal parts, each having value of θ.
Therefore, θ = 45o. And hence lines AC and AB subtend equal angles (θ) at x-axis.
Slope of AC = tan θ =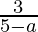 . . . . (1)
. . . . (1)
Slope of AB = tan (180−θ) =
=> −tan θ =
=> tan θ =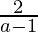 . . . . (2)
. . . . (2)
From (1) and (2), we get,
=>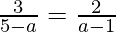
=> 3a – 3 = 10 – 2a
=> a = 13/5
Therefore, the coordinates of point A are (13/5, 0).
Question 23. Prove that the product of the lengths of the perpendiculars drawn from the points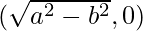 and
and to the line
to the line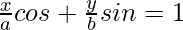 is b2.
is b2.
Solution:
We are given the line,
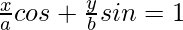
=> bx cos θ + ay sin θ – ab = 0 . . . . (1)
Now, we know that the perpendicular distance(d) of a line Ax + By + C = 0 from (x, y) is given by,
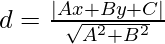
So, perpendicular distance(d1) of (1) from point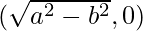 is,
is,

=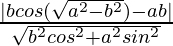
And the perpendicular distance(d2) of (1) from point is,
is,
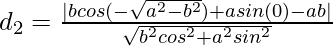
=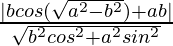
Now, L.H.S. = d1d2
=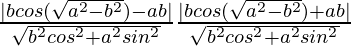
=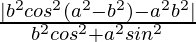
=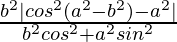
=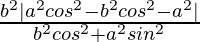
=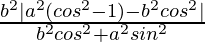
=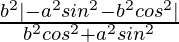
=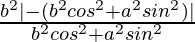
=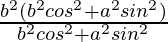
= b2
= R.H.S.
Hence, proved.
Question 24. A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find the equation of the path that he should follow.
Solution:
We are given that,
2x – 3y + 4 = 0 . . . . (1)
3x + 4y – 5 = 0 . . . . (2)
6x – 7y + 8 = 0 . . . . (3)
It is given that the person is standing at the intersection of the paths represented by lines (1) and (2).
By solving equations (1) and (2) we get
x = –1/17 and y = 22/17
As perpendicular distance is the shortest distance, the person can reach path (3) in the least time if he walks along the perpendicular line to (3) from point (–1/17, 22/17).
Now, the slope of the line (3) = 6/7
Hence, the slope of the line perpendicular to line (3) = –1/(6/7) = –7/6
So the equation of line passing through (–1/17, 22/17) and having a slope of –7/6 is given by,
=>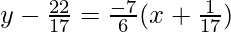
=> 6 (17y – 22) = –7 (17x + 1)
=> 102y – 132 = –119x – 7
=> 1119x + 102y = 125
Therefore, the required path is 119x + 102y = 125.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...