Class 10 RD Sharma Solutions – Chapter 6 Trigonometric Identities – Exercise 6.1 | Set 1
Last Updated :
30 Apr, 2021
Prove the following trigonometric identities:
Question 1. (1 – cos2 A) cosec2 A = 1
Solution:
We have,
L.H.S. = (1 – cos2 A) cosec2 A
By using the identity, sin2 A + cos2 A = 1, we get,
= (sin2 A) (cosec2 A)
= sin2 A × (1/sin2 A)
= 1
= R.H.S.
Hence proved.
Question 2. (1 + cot2 A) sin2 A = 1
Solution:
We have,
L.H.S. = (1 + cot2 A) sin2 A
By using the identity, cosec2 A = 1 + cot2 A, we get,
= cosec2 A sin2 A
= (1/sin2 A) × sin2 A
= 1
= R.H.S
Hence proved.
Question 3. tan2 θ cos2 θ = 1 − cos2 θ
Solution:
We have,
L.H.S. = tan2 θ cos2 θ
= (sin2 θ/cos2 θ) (cos2 θ)
= sin2 θ
= 1 − cos2 θ
= R.H.S.
Hence proved.
Question 4. cosec θ √(1 – cos2 θ) = 1
Solution:
We have,
L.H.S. = cosec θ √(1 – cos2 θ)
= cosec θ √(sin2 θ)
= cosec θ sin θ
= (1/sin θ) (sin θ)
= 1
= R.H.S.
Hence proved.
Question 5. (sec2 θ − 1)(cosec2 θ − 1) = 1
Solution:
We have,
L.H.S. = (sec2 θ − 1)(cosec2 θ − 1)
By using the identities sec2 θ − tan2 θ = 1 and cosec2 θ − cot2 θ = 1, we have,
= tan2 θ cot2 θ
= (tan2 θ) (1/tan2 θ)
= 1
= R.H.S.
Hence proved.
Question 6. tan θ + 1/tan θ = sec θ cosec θ
Solution:
We have,
L.H.S. = tan θ + 1/ tan θ
= (tan2 θ + 1)/tan θ
= sec2 θ/tan θ
= 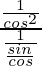
= 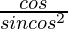
= 1/sin θ cos θ
= sec θ cosec θ
= R.H.S.
Hence proved.
Question 7. cos θ/(1 – sin θ) = (1 + sin θ)/cos θ
Solution:
We have,
L.H.S. = cos θ/(1 – sin θ)
= 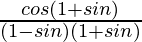
= 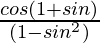
= 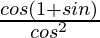
= (1 + sin θ)/cos θ
= R.H.S.
Hence proved.
Question 8. cos θ/(1 + sin θ) = (1 – sin θ)/cos θ
Solution:
We have,
L.H.S. = cos θ/(1 + sin θ)
= 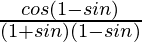
= 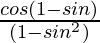
= 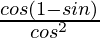
= (1 – sin θ)/cos θ
= R.H.S.
Hence proved.
Question 9. cos2 θ + 1/(1 + cot2 θ) = 1
Solution:
We have,
L.H.S. = cos2 θ + 1/(1 + cot2 θ)
= cos2 θ + 1/(cosec2 θ)
= cos2 θ + sin2 θ
= 1
= R.H.S.
Hence proved.
Question 10. sin2 A + 1/(1 + tan2 A) = 1
Solution:
We have,
L.H.S. = sin2 A + 1/(1 + tan2 A)
= sin2 A + 1/(sec2 A)
= sin2 A + cos2 A
= 1
= R.H.S.
Hence proved.
Question 11. 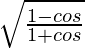 = cosec θ − cot θ
= cosec θ − cot θ
Solution:
We have,
L.H.S. = 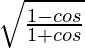
= 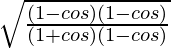
= 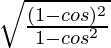
= 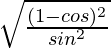
= 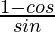
= 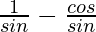
= cosec θ − cot θ
= R.H.S.
Hence proved.
Question 12. (1 – cos θ)/sin θ = sin θ/(1 + cos θ)
Solution:
We have,
L.H.S. = (1 – cos θ)/sin θ
= 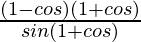
= 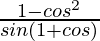
= 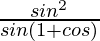
= sin θ/(1 + cos θ)
= R.H.S.
Hence proved.
Question 13. sin θ/(1 – cos θ) = cosec θ + cot θ
Solution:
We have,
L.H.S. = sin θ/(1 – cos θ)
= 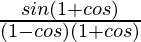
= 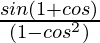
= 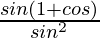
= 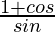
= 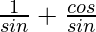
= cosec θ + cot θ
= R.H.S.
Hence proved.
Question 14. (1 – sin θ)/(1 + sin θ) = (sec θ – tan θ)2
Solution:
We have,
L.H.S. = (1 – sin θ)/(1 + sin θ)
= 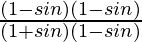
= 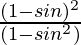
= 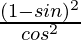
= 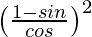
= 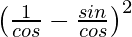
= (sec θ – tan θ)2
= R.H.S.
Hence proved.
Question 15. 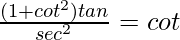
Solution:
We have,
L.H.S. = 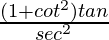
= 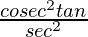
= 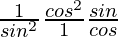
= cos θ/sin θ
= cot θ
= R.H.S.
Hence proved.
Question 16. tan2 θ − sin2 θ = tan2 θ sin2 θ
Solution:
We have,
L.H.S. = tan2 θ − sin2 θ
= sin2 θ/cos2 θ − sin2 θ
= sin2 θ(1/cos2 θ − 1)
= 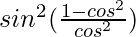
= sin2θ (sin2θ/cos2θ)
= tan2 θ sin2 θ
= R.H.S.
Hence proved.
Question 17. (cosec θ + sin θ)(cosec θ – sin θ) = cot2θ + cos2θ
Solution:
We have,
L.H.S. = (cosec θ + sin θ)(cosec θ – sin θ)
= cosec2 θ – sin2 θ
= (1 + cot2 θ) – (1 – cos2 θ)
= 1 + cot2 θ – 1 + cos2 θ
= cot2 θ + cos2 θ
= R.H.S.
Hence proved.
Question 18. (sec θ + cos θ) (sec θ – cos θ) = tan2 θ + sin2 θ
Solution:
We have,
L.H.S. = (sec θ + cos θ) (sec θ – cos θ)
= sec2 θ – cos2 θ
= (1 + tan2 θ) – (1 – sin2 θ)
= 1 + tan2 θ – 1 + sin2 θ
= tan2 θ + sin2 θ
= R.H.S
Hence proved.
Question 19. sec A(1 – sin A) (sec A + tan A) = 1
Solution:
We have,
L.H.S. = sec A(1 – sin A) (sec A + tan A)
= 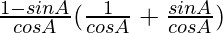
= 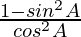
= 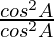
= 1
= R.H.S
Hence proved.
Question 20. (cosec A – sin A)(sec A – cos A)(tan A + cot A) = 1
Solution:
We have,
L.H.S. = (cosec A – sin A)(sec A – cos A)(tan A + cot A)
= 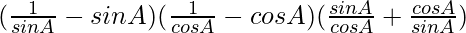
= 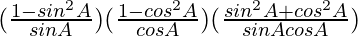
= 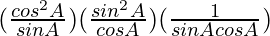
= 1
= R.H.S
Hence proved.
Question 21. (1 + tan2 θ)(1 – sin θ)(1 + sin θ) = 1
Solution:
We have,
L.H.S. = (1 + tan2 θ)(1 – sin θ)(1 + sin θ)
= (sec2 θ) (1 – sin2 θ)
= (sec2 θ) (cos2 θ)
= 1
= R.H.S
Hence proved.
Question 22. sin2 A cot2 A + cos2 A tan2 A = 1
Solution:
We have,
L.H.S. = sin2 A cot2 A + cos2 A tan2 A
= sin2 A (cos2 A/sin2 A) + cos2 A (sin2 A/cos2 A)
= cos2 A + sin2 A
= 1
= R.H.S.
Hence proved.
Question 23.
(i) cot θ – tan θ = 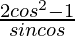
Solution:
We have,
L.H.S. = cot θ – tan θ
= cos θ/sin θ – sin θ/cos θ
= 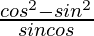
= 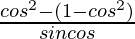
= 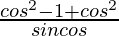
= 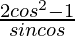
= R.H.S.
Hence proved.
(ii) tan θ – cot θ = 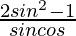
Solution:
We have,
L.H.S. = tan θ – cot θ
= sin θ/cos θ – cos θ/sin θ
= 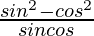
= 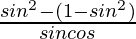
= 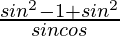
= 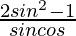
= R.H.S.
Hence proved.
Question 24. (cos2 θ/sin θ) – cosec θ + sin θ = 0
Solution:
We have,
L.H.S. = (cos2 θ/sin θ) – cosec θ + sin θ
= 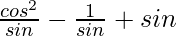
= 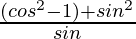
= 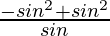
= 0
= R.H.S.
Hence proved.
Question 25. 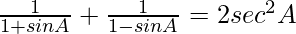
Solution:
We have,
L.H.S. = 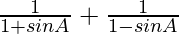
= 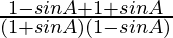
= 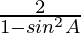
= 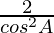
= 2 sec2 A
= R.H.S.
Hence proved.
Question 26. 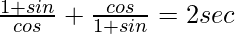
Solution:
We have,
L.H.S. = 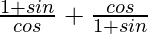
= 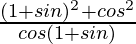
= 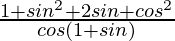
= 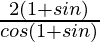
= 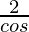
= 2 sec θ
= R.H.S.
Hence proved.
Question 27. 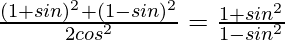
Solution:
We have,
L.H.S. = 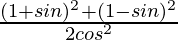
= 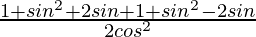
= 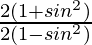
= 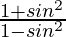
= R.H.S.
Hence proved.
Question 28. 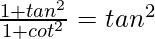
Solution:
We have,
L.H.S. = 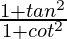
= sec2 θ/cosec2 θ
= 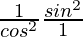
= tan2 θ
= R.H.S.
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...