Class 10 RD Sharma Solutions – Chapter 5 Trigonometric Ratios – Exercise 5.3 | Set 2

Question 8. Prove the following:

(i) sin θ sin (90° – θ) – cosθ cos (90° – θ) = 0

Solution:

We have to prove that  sin θ sin (90° – θ) – cosθ cos (90° – θ) = 0

Taking LHS

= sin θ sin (90° – θ) – cosθ cos (90° – θ)           -(∵ sin (90° – θ) = cos θ)

= sin θ cosθ – cosθ sinθ

= 0

LHS = RHS 

Hence proved

(ii)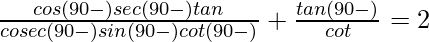 

Solution:

We have to prove that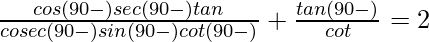 

Taking LHS 

= 

= 

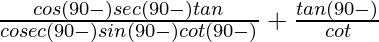
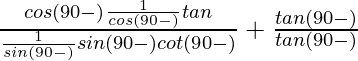
= tan θ/tan θ + cot θ/cot θ

= 1 + 1

= 2 

LHS = RHS 

Hence Proved

(iii)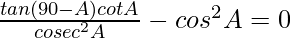 

Solution:

We have to prove that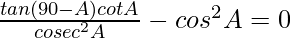 

Taking LHS

= 

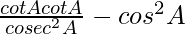
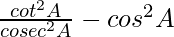=              -(∵ cot θ = cosθ/sinθ and cosecθ = 1/sinθ)

= 

= 

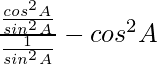
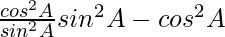
= cos²A – cos²A

= 0

LHS = RHS 

Hence Proved

(iv)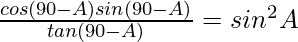 

Solution:

We have to prove that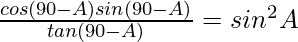 

Taking LHS

= 

= 

= 

= 

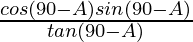
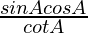
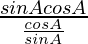
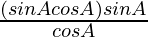
= sin²A

LHS = RHS 

Hence Proved

(v) sin (50° + θ) – cos (40° – θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89° = 1  

Solution:

We have to prove that sin (50° + θ) – cos (40° – θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89° = 1  

Taking LHS

= sin (50° + θ) – cos (40° – θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89°

= cos(90° – (50° + θ)) – cos (40° – θ) + tan (90° – 89°) tan (90° – 80°) tan (90° – 70°) tan 70° tan 80° tan 89°

= cos (40° – θ) – cos (40° – θ) + cot 89° cot 80° cot 70° tan 70° tan 80° tan 89°

= 0 + 1 = 1 

LHS = RHS

Hence Proved

Question 9. Evaluate:

(i) 2/3(cos⁴30° – sin⁴45°) – 3(sin²60° – sec²45°) + 1/4cot²30°

Solution:

Given: 2/3(cos⁴30° – sin⁴45°) – 3(sin²60° – sec²45°) + 1/4cot²30°

= 

= 

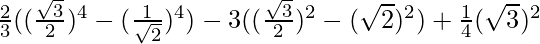
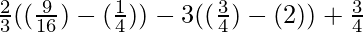
= 2/3(5/16) – 3(-5/4) + 3/4

= 5/24 + 90/24 + 18/24

= 113/24

Hence, 2/3(cos⁴30° – sin⁴45°) – 3(sin²60° – sec²45°) + 1/4cot²30° = 113/24

(ii) 4(sin⁴30° + cos⁴60°) – 2/3(sin²60° – cos²45°) + 1/2tan²60°

Solution:

Given: 4(sin⁴30° + cos⁴60°) – 2/3(sin²60° – cos²45°) + 1/2tan²60°

= 

= 

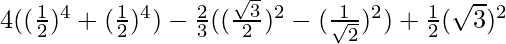
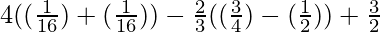
= 4(2/16) – 2/3(1/4) + 3/2

= 1/2 – 1/6 + 3/2

= 4/2 – 1/6

= 2 – 1/6

= (12 – 1)/6 

= 11/6

Hence, 4(sin⁴30° + cos⁴60°) – 2/3(sin²60° – cos²45°) + 1/2tan²60° = 11/6

(iii) sin 50°/cos 40° + cosec 40° / sec 50° – 4cos 50° cosec40°

Solution:

Given: sin 50°/cos 40° + cosec 40° / sec 50° – 4cos 50° cosec40°

= 

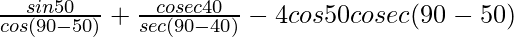
= sin 50°/sin 50° + cosec 40° / cosec 40° – 4cos 50° sec50°

= 1 + 1 – 4

= -2

Hence, sin 50°/cos 40° + cosec 40° / sec 50° – 4cos 50° cosec40° = -2

(iv) tan35°tan40°tan45°tan50°tan55°

Solution:

Given: tan35°tan40°tan45°tan50°tan55°

= tan(90° – 55°)tan(90° – 50°)tan45°tan50°tan55°

= cot55°cot50°tan45°tan50°tan55°

= (1/tan55°)(1/tan50°)tan45°tan50°tan55°

= 1

Hence, tan35°tan40°tan45°tan50°tan55° = 1

(v) cosec(65° + θ) – sec(25° – θ) – tan(55° – θ) + cot(35° + θ)

Solution:

Given: cosec(65° + θ) – sec(25° – θ) – tan(55° – θ) + cot(35° + θ)

= cosec(65° + θ) – cosec(90° – (25° – θ)) – tan(55° – θ) + tan(90° – (35° + θ))

= cosec(65° + θ) – cosec(90° – 25° + θ) – tan(55° – θ) + tan(90° – 35° – θ)

= cosec(65° + θ) – cosec(65° + θ) – tan(55° – θ) + tan(55° – θ)

= 0

Hence, cosec(65° + θ) – sec(25° – θ) – tan(55° – θ) + cot(35° + θ) = 0

(vi) tan7°tan23°tan60°tan67°tan83°

Solution:

Given: tan7°tan23°tan60°tan67°tan83°

= tan(90° – 83°)tan(90° – 67°)tan60°tan67°tan83°

= cot83°cot67°tan60°tan67°tan83°

= (1/tan83°)(1/tan67°)tan60°tan67°tan83°

= tan60°

= √3

Hence, tan7°tan23°tan60°tan67°tan83° = √3

(vii)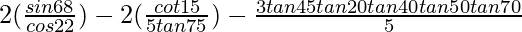 

Solution:

Given: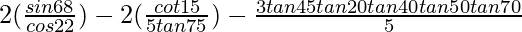 

= 

= 

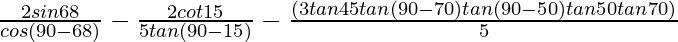
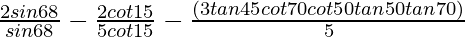
= 2 – 2/5 – 3/5

= (10 – 2 – 3)/5 

= 5/5

= 1

Hence, 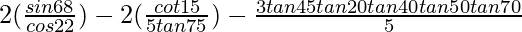 = 1

(viii)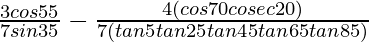 

Solution:

Given: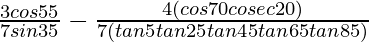 

= 

= 

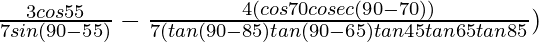
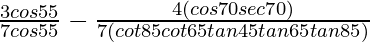
= 3/7 – 4/7

= -1/7

Hence, 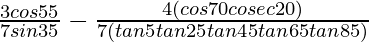 = -1/7

(ix) sin18°/cos72° + √3(tan10°tan30°tan40°tan50°tan80°)

Solution:

Given: sin18°/cos72° + √3(tan10°tan30°tan40°tan50°tan80°)

= sin18°/cos(90° – 18°) + √3(tan(90° – 80°)tan(90° – 50°)tan30°tan50°tan80°)

= sin18°/sin18° + √3(cot80°cot50°tan30°tan50°tan80°)

= 1 + √3tan30°

= 1 + √3(1/√3)

= 2

Hence, sin18°/cos72° + √3(tan10°tan30°tan40°tan50°tan80°) = 2

(x)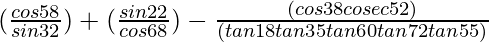 

Solution:

Given: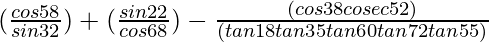 

= 

= 

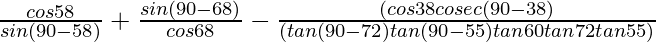
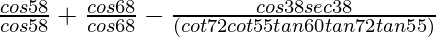
= 1 + 1 – 1/tan60°

= 2 – 1/√3

= (2√3 – 1)/√3

= (6 – √3)/3

Hence, 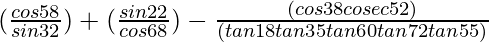= (6 – √3)/3

Question 10. If sin θ = cos(θ − 45°), where θ and θ−45° are acute angles, find the degree measure of θ.

Solution:

Given: sinθ = cos(θ − 45°), where θ and θ−45° are acute angles

= sinθ = cos(θ − 45°)           -(∵ sinθ = cos(90 − θ))

= cos(90° − θ) = cos(θ − 45°)

Equating the angles

(90° − θ) = (θ − 45°)

2θ = 90° + 45° = 135°

θ = 135°/2

θ = 67°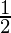

Question 11. If A, B, C are the interior angles of a triangle ABC, show that

(i) sin (B + C)/2 = cos A/2  

Solution:

According to question

In a triangle ABC, A, B, C are the interior angles

So, the sum of interior angles = A + B + C = 180°

B +C  = 180° – A

We have  

sin (B + C)/2 = cos A/2  

Taking LHS  

sin (B + C)/2          -(1)

Putting the value of B + C in equation(1)

= sin (180° – A)/2

= sin (90° – A/2)

= cos A/2

LHS = RHS 

Hence Proved

(ii) cos (B + C)/2 = sin A/2  

Solution:

According to question

In a triangle ABC, A, B, C are the interior angles

So, the sum of interior angles = A + B + C = 180°

B + C = 180° – A

We have  

cos (B + C)/2 = sin A/2  

Taking LHS  

cos (B + C)/2          -(1)

Putting the value of B + C in equation(1)

= cos (180° – A)/2

= cos (90° – A/2)

= sin A/2 

LHS = RHS 

Hence Proved

Question 12. If 2θ + 45° and 30° − θ are acute angles, find the degree measure of θ satisfying sin(2θ + 45°) = cos(30° − θ).

Solution:

Given: 2θ + 45° and (30° − θ) are acute and sin(2θ + 45°) = cos(30° − θ)

We have,

sin(2θ + 45°) = cos(30° − θ)

sin(2θ + 45°) = sin(90° − (30° − θ))           -(∵ cosθ = sin(90° − θ))

sin(2θ + 45°) = sin(60° + θ)                          

Now equating the angles

2θ + 45° = 60° + θ

2θ − θ = 60° − 45°

θ = 15°

Question 13. If θ is a positive acute angle such that secθ = cosec60°, find the value of 2cos²θ − 1.

Solution:

Given, θ is acute and secθ = cosec60°

Find the value of 2cos²θ − 1       -(1)

cosec60° = 2/√3

or secθ = 2/√3

We know that, sec30° = 2/√3

secθ = sec30°

θ = 30°

Putting the value of θ in eq(1), we get

= 2cos²30° − 1

= 2(√3/2)² − 1

= 2(3/4) − 1

= 3/2 − 1

= 1/2

Hence, the value of 2cos²θ − 1 = 1/2

Question 14. If cos2θ = sin4θ, where 2θ and 4θ are acute angles, find the value of θ.

Solution:

Given: 2θ and 4θ are acute and cos2θ = sin4θ

So, we have,  

cos2θ = sin(90° − 2θ)           -(∵ sin (90° – θ) = cos θ)

Now, sin(90° − 2θ) = sin4θ

Equating the angles

90° − 2θ = 4θ

90° = 2θ + 4θ

6θ = 90°

θ = 15°

Hence, the value of θ = 15°

Question 15. If sin3θ = cos (θ − 6°), where 3 θ and θ − 6° are acute, find the value of θ.

Solution:

Given: 3θ and (θ − 6°) are acute and sin3θ = cos(θ − 6°)

So, we have,                                                                                              

cos(θ − 6°) = sin(90° − (θ − 6°)) = sin(96° − θ).         -(∵ cosθ = sin(90° − θ))

Now, sin3θ = sin(96° − θ)

Equating the angles

3θ = 96° − θ

3θ + θ = 96°

4θ = 96°

θ = 96°/4

θ = 24°

Hence, the value of θ = 24°

Question 16. If sec4A = cosec(A – 20°), where 4A is an acute angle, find the value of A.

Solution:

Given: 4A is acute and sec4A = cosec(A − 20°)

So, we have,  

sec4A = cosec(90° − 4A)         -(∵ secθ = cosec(90° − θ))

Now, cosec(90° − 4A) = cosec(A − 20°)

Equating the angles

(90° − 4A) = (A − 20°)

110° = 5A

5A = 110°

A = 110°/5

A = 22°

Hence, the value of A = 22°

Question 17. If sec2A = cosec(A – 42°), where 2A is an acute angle, find the value of A.

Solution:

Given: 2A is acute and sec2A = cosec(A − 42°)

So, we have,  

sec2A = cosec(90° − 2A)          -(∵ secθ = cosec(90° − θ))

Now, cosec(90° − 2A) = cosec(A − 42°)

Equating the angles

(90° − 2A) = (A − 42°)

132° = 3A

3A = 132°

A = 132°/3

A = 44°

Hence, the value of A = 44°