Class 10 RD Sharma Solutions – Chapter 5 Trigonometric Ratios – Exercise 5.2 | Set 3

Question 27. If A = B = 60°, verify that

(i) cos(A − B) = cos A cos B + sin A sin B

Solution: 

We know sin 60° = √3/2, sin 30° = 1/2

Putting the values of A and B in the equation below

cos(60° − 60°) = cos60°cos60° + sin60°sin60°

cos(0) = cos²60° + sin²60°

1 = (1/2)² + (√3/2)²

1 = 1/4 + 3/4

1 = 4/4 = 1 

Hence Proved

(ii) sin(A − B) = sin A cos B − cos A sin B

Solution:

Putting the values of A and B in the equation below

sin(60° − 60°) = sin60°cos60° − cos60°sin60°

sin(0°) = (1/2)(√3/2) – (√3/2)(1/2) 

0 = √3/4 – √3/4

0 = 0  

Hence Proved

(iii) tan(A − B) =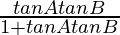 

Solution:

Putting the values of A and B in the equation below

tan(60° − 60°) =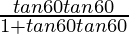 

tan0 =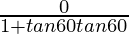

0 = 0 

Hence Proved

Question 28. If A = 30° and B = 60°, verify that

(i) sin(A + B) = sin A cos B cos A sin B

Solution:

We know sin 60° = cos 30° = √3/2, sin 30° = cos 60° = 1/2

Putting the values of A and B in the following equations

sin(30° + 60°) = sin 30° cos 60° cos 30° sin 60°

sin 90° = (1/2)(1/2) + (√3/2)(√3/2)

1 = 1/4 + 3/4

1 = 1 

Hence Proved

(ii) cos(A + B) = cos A cos B − sin A sin B

Solution:

Putting the values of A and B in the following equations

cos(30° + 60°) = cos 30° cos 60° – sin 30° sin 60°

cos 90° = (√3/2)(1/2) – (1/2)(√3/2)

0 = √3/4 – √3/4

0 = 0 

Hence Proved

Question 29. If sin(A + B) = 1 and cos(A − B) = 1, 0° < A + B ≤ 90° and A ≥ B, find A and B.

Solution:

Given sin(A + B) = 1, cos(A − B) = 1, 0° < A + B ≤ 90° and A ≥ B,

We know that, sin90° = 1 and cos0° = 1

sin(A + B) = 1 and sin90∘= 1

We can say that

(A + B) = 90°          -(1)

cos(A − B) = 1 and cos0° = 1

(A − B) = 0°

A = B          -(2)   

Substituting eq(2) in (1)

A + A = 90°

2A = 90°

A = 45°

A = B = 45°

Question 30. If tan(A + B) = √3 and tan(A − B) = 1/√3, 0° < A + B ≤ 90°; A > B, find A and B.

Solution:

Given tan(A + B) = √3

tan(A − B) = 1/√3

0∘< A + B ≤ 90∘and A > B,

We know that, tan30° = 1/√3 and tan60° = √3 

Now,

tan(A + B) = √3 and tan60 = √3

(A + B) = 60°          -(1)

Again,

tan(A − B) = 1/√3 and tan30° = 1/√3

(A − B) = 30°          -(2)

Solving eq(1) and (2),

(A + B) = 60°

(A − B) = 30°

Solving the above two equations we get

2A = 90°

A = 90°/2 = 45°

Question 31. If sin(A – B) = 1/2 and cos(A + B) = 1/2, 0° < A + B ≤ 90°; A < B, find A and B.

Solution:

Given, sin(A − B) = 1/2

cos(A + B) = 1/2

0° < A + B ≤ 90° and A < B,

We know that, sin30° = 1/2and cos60° = 1/2

Since sin(A − B) = 1/2 and sin30° = 1/2

So (A − B) = 30°          -(1)

Again  

cos(A + B) = 1/2 and cos60° = 1/2

So (A + B) = 60°          -(2)

Solving eq(1) and (2) we get

2A = 90°

A = 90°/2 = 45°

From (2)

(A + B) = 60°

Also, A = 45°

B = 60° − 45°

B = 15°

Therefore, A = 45°, B = 15°

Question 32. In a ∆ABC right-angled at B, ∠A = ∠C. Find the values of

(i) sin A cos C + cos A sin C

Solution:

Given: In ∆ABC right-angled at B, ∠A = ∠C

We know in a triangle ∠A + ∠B +∠C = 180°

2∠A = 180° – 90° = 45°               [∠B = 90°]

Now,

We have sin A cos C + cos A sin C

Putting the values of each angle 

sin 45° cos 45° + cos 45° sin 45° 

= (1/√2)(1/√2) + (1/√2)(1/√2)

= 1/2 + 1/2

= 1

(ii) sin A sin B + cos A cos B

Solution:

We have sin A sin B + cos A cos B

Putting the values of each angle  

sin 45° sin 90° + cos 45° cos 90°  

= (1/√2)(1) + (1/√2)(0)

= (1/√2) + 0

= 1/√2

Question 33. Find acute angles A and B, if sin(A + 2B) = √3/2 and cos(A + 4B) = 0, and A > B.

Solution:

Given, sin(A + 2B) = √3/2, cos(A + 4B) = 0, A > B,

We know that, sin60° = √3/2 and cos90° = 0

Since sin(A + 2B) = √3/2 and sin60° = √3/2

So (A + 2B) = 60°          -(1)

Again cos(A + 4B) = 0 and cos90° = 0

So (A + 4B) = 90°          -(2)

From (1) from (2) we get,

2B = 30°

B = 30°/2 = 15°

From (2)

(A + 4B) = 90°

Also, B = 15°

A = 90° − 60°

A = 30°

Therefore, A = 30°, B = 15°

Question 34. In ΔPQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.

Solution:

Given In ΔPQR, right-angled at Q, PQ = 3 cm and PR = 6 cm.

We know cos P = Base/Hypotenuse =3/6

cos 60° = 1/2

So ∠P = 60°

In ΔPQR 

∠P + ∠Q + ∠R = 180°

∠R = 180° – 90° – 60°

∠R = 30°

Therefore, ∠P = 60°, ∠R = 30°

Question 35. If sin(A − B) = sin A cos B − cos A sin B and cos(A − B) = cos A cos B + sin A sin B, find the values of sin15° and cos15°.

Solution:

To find sin15°:

We have sin15° = sin(45° – 30°)

A = 45°and B = 30°

Now putting the values of A and B in the following equation

sin(A − B) = sin A cos B − cos A sin B

sin(45° − 30°) = sin 45° cos 30° − cos 45° sin 30°

sin15° = (1/√2)(√3/2) – (1/√2)(1/2))

sin15° = (√3 – 1)/2√2 

To find cos15°:

 cos15° = cos(45° – 30°)

A = 45° and B = 30°

Again putting the values of A and B in the following equation

 cos(A − B) = cos A cos B + sin A sin B

cos(45° − 30°) = cos 45° cos 30° + sin 45° sin 30°

sin15° = (1/√2)(√3/2) + (1/√2)(1/2))

sin15° = (√3 + 1)/2√2   

Question 36. In a right △ABC, right-angled at C, if ∠B = 60° and AB = 15 units. Find the remaining angles and sides.

Solution:

Given In a right △ABC right-angled at C, ∠B = 60° ∠C = 90°

We know in a triangle ∠A + ∠B + ∠C = 180°

∠A = 180° – 150° = 30°

sin 30° = BC/AB = BC/15 

BC/15 = 1/2

BC = 7.5 units

cos 30° = AC/AB = AC/15

AC/15 = √3/2

AC = 15√3/2 units

Question 37. If ΔABC is a right triangle such that ∠C = 90°, ∠A = 45°, and BC = 7 units. Find ∠B, AB, and AC.

Solution:

Given: In ΔABC ∠C = 90°, ∠A = 45°, and BC = 7 units

We know in a triangle ∠A + ∠B + ∠C = 180°

∠B = 180° – 135° = 45°

cos B = BC/AB = 7/AB

cos 45° = 7/AB

7/AB = 1/√2

AB = 7/√2 units

tan A = BC/AC

tan 45° = 7/AC

7/AC = 1

AC = 7 units

Question 38. In a rectangle ABCD, AB = 20 cm, ∠BAC = 60°, calculate side BC and diagonals AC, BD.

Solution:

Given: rectangle ABCD, AB = 20 cm, ∠BAC = 60°

tan 60° = BC/AC

√3 = BC/20

BC = 20√3 cm

cos 60° = AB/AC

1/2 = 20/AC

AC = 40 cm

In rectangle both diagonals are equal

Question 39. If A and B are acute angles such that tan A = 1/2, tan B = 1/3, and tan(A + B) = 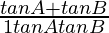 find (A + B). 

Solution:

Given, A and B are acute angles such that tanA = 1/2 and tanB = 1/3

tan(A + B) =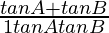 

tan(A + B) =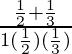 

tan(A + B) =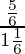 

tan(A + B) = 

tan(A + B) = 1

We know, tan45° = 1

Therefore, (A + B) = 45°

Question 40. Prove that (√3 + 1)(3 – cot 30°) = tan³ 60° – 2sin 60°

Solution:

Taking R.H.S

tan³ 60° – 2sin 60°

(√3) – 2(√3/2) = 3√3 – √3 = 2√3

Now taking L.H.S

(√3 + 1)(3 – cot 30°) 

= (√3 + 1)(3 – √3) 

= (√3 + 1)√3(√3 – 1) 

= 2√3

L.H.S = R.H.S

Hence Proved