Class 10 RD Sharma Solutions – Chapter 5 Trigonometric Ratios – Exercise 5.2 | Set 2

Evaluate each of the following(14-19)

Question 14.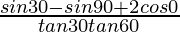 

Solution: 

Given: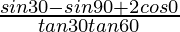           -(1)

Putting the values of sin 30° = 1/2, tan 30° = 1/√3, tan 60° = √3, sin 90° = cos 0° = 1 in eq(1) 

= 

= 

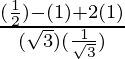
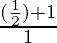
= 3/2 

Question 15.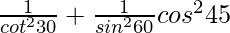 

Solution:  

Given: 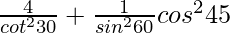           -(1)

= tan²30° + cosec²60° − cos²45°

Putting the values of cosec60° = 2/√3, cos45° = 1/√2, tan30° = 1/√3 in eq(1)  

= 

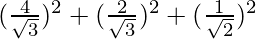
= 4/3 + 4/3 – 1/2

= (4 + 4)/3 – 1/2

= 8/3 – 1/2

= 13/6

Question 16. 4(sin⁴30° + cos²60°) – 3(cos²45° – sin²90°) – sin²60°

Solution:

Given: 4(sin⁴30° + cos²60°) – 3(cos²45° – sin²90°) – sin²60°       -(1)

Putting the values of cos45° = 1/√2, sin30° = cos30° = 1/2, sin60° = √3/2, sin90° = 1 in eq(1)

= 4((1/2)⁴ + (1/2)²) – 3((1/√2)² – (1)²) – (√3/2)²

= 4((1/16) + (1/4)) – 3((1/2) – 1) – (3/4)

= 4(5/16) – 3(-1/2) – 3/4

= 5/4 + 3/2 – 3/4

= (5 + 6 – 3)/4

= 8/4

= 2

Question 17.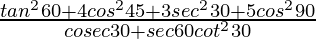 

Solution:

Given: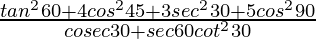 

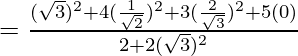
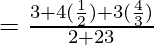
= 3 + 4(1/2) + 3(4/3)

= 3 + 2 + 4

= 9

Question 18.  Evaluate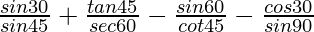 

Solution:

Given: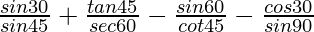 

= 

= 

= 

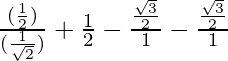
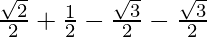
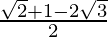
Question 19.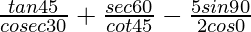 

Solution:

Given: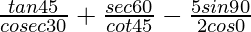 

As we know that 

cosecθ = 1/sinθ, cotθ = 1/tanθ

Now,

= tan45°sin30° + sec60°tan45° –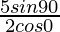 

= 1 – 1/2 + 2 – 5/2

= (1 – 5)/2 + 2

= -2 + 2

= 0

Find the value of X in each of the following 

Question 20. 2sin3x = √3

Solution:

Given,

2sin3x = √3

sin3x = √3/2

As we know that,

sin60° = √3/2

So, sin3x = sin60°

Now, 

3x = 60°

x = 60°/3

x = 20°

Question 21. 2sin x/2

Solution:

Given

2sinx/2 = 1 or sin x/2 = 1/2

We know sin30° = 1/2

So, 

sinx/2 = sin30°

x/2 = 30°

x = 60°

Question 22. √3sinx = cosx

Solution:

Given,

√3sinx = cosx or sinx/cosx = 1/√3

tan x = 1/√3

We know tan30° = 1/√3

So,

tan x = tan30°

x = 30°

Question 23. tan x = sin45°cos45° + sin30°

Solution:

Given: tan x = sin45°cos45° + sin30°

Putting the values of sin 45° = cos 45° = 1/√2, sin 30° = 1/2

tan x = ((1/√2 × 1/√2) + 1/2) 

tan x = (1/√2)² + 1/2

tan x = 1/2 + 1/2

tan x = 1

tan x = tan45°

So, x = 45°

Question 24. √3tan 2x = cos60° + sin45°cos45°

Solution:

Putting the values of sin 45° = cos 45° = 1/√2, cos 60° = 1/2 in the given equation  

√3tan 2x = 1/2 + 1/√2 × 1/√2

√3tan 2x = 1/2 + (1/√2)²

√3tan 2x = 1/2 + 1/2

tan 2x = 1/√3

tan 2x = tan30°

So, x = 15°

Question 25. cos 2x = cos60°cos30° + sin60°sin30°

Solution:

Given: cos 2x = cos60°cos30° + sin60°sin30°

Putting the values of sin 30° = cos 60° = 1/2, cos 30° = sin 60° = √3/2

cos 2x = 1/2 × √3/2 + √3/2 × 1/2

cos 2x = √3/4 + √3/4

cos 2x = √3/2

cos 2x = cos30°

So, x = 15°

Question 26. If θ = 30°, verify that:

(i) tan2θ =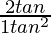 

Solution:

Putting the value of given θ in the above equation

We get

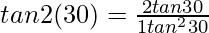
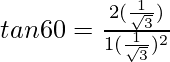
√3 =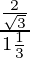 

√3 =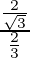 

√3 = √3

Hence Proved

(ii) tan2θ =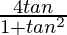 

Solution:

Putting the value of given θ in the above equation

We get

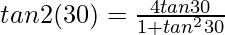
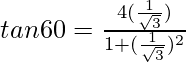
√3 =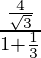 

√3 =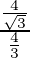 

√3 = √3 

Hence Proved

(iii) cos2θ =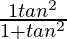 

Solution:

Putting the value of given θ in the above equation

We get

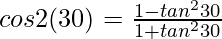
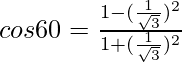
1/2=(3-1)(3+1)

1/2 = 2/4 or 1/2

Hence Proved

(iv) cos3θ = 4cos³θ − 3cosθ

Solution:

Putting the value of given θ in the above equation

We get

cos3(30°) = 4cos³ 30° − 3cos 30°

cos 90° = 4cos³30° − 3cos 30°

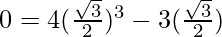
0 = 4(3√3/8) – 4(3√3/8)

0 = 3(√3/2) – 3(√3/2)

0 = 0

Hence Proved