Open In App

Class 10 RD Sharma Solutions – Chapter 5 Trigonometric Ratios – Exercise 5.1 | Set 2

Last Updated : 21 Feb, 2021
Improve
Improve
Like Article
Like
Save
Share
Report

Question 7. If cotθ = 7/8, evaluate:

(i) 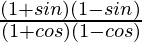\frac{(1+sinθ)(1-sinθ)}{(1+cosθ)(1-cosθ)}                              

(ii) cot2θ 

Solution:

 cotθ = 7/8 = Base/Perpendicular

In right-angled ΔPQR,

∠Q = 90°, PQ = 8, RQ = 7

Using Pythagoras Theorem

PR2 = PQ2 + QR2

PR2 = 82 + 72 = 64 + 49

PR2 = 113

PR = √113
Now

sinθ = Perpendicular/Hypotenuse = PQ/PR = 8/√113     

cosθ = Base/Hypotenuse = QR/PR = 7/√113            

(i) 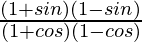\frac{(1+sinθ)(1-sinθ)}{(1+cosθ)(1-cosθ)}

Putting the values of sinθ and cosθ in the equation

=\frac{(1+\frac{8}{\sqrt113})(1-\frac{8}{\sqrt113})}{(1+\frac{7}{\sqrt113} )(1-\frac{7}{\sqrt113} )}

=\frac{(1)^2-(\frac{8}{\sqrt113})^2}{(1)^2-(\frac{7}{\sqrt113})^2}

=\frac{1-\frac{64}{113}}{1-\frac{49}{113}}

=\frac{\frac{113-64}{113}}{\frac{113-49}{113}}

=\frac{\frac{49}{113}}{\frac{64}{113}}

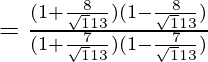
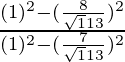
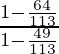
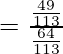
= 49/64

(ii) cot2θ  

= (cosθ/sinθ)2 

Putting the values of sinθ and cosθ in the following equation

=[\frac{(\frac{7}{\sqrt113})}{(\frac{8}{\sqrt113})}]^2

=\frac{(\frac{49}{113})}{(\frac{64}{113})}

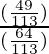
= 49/64

or

cot2θ = (cotθ)2 = (7/8)2 = 49/64

Question 8. If 3 cot A = 4, check whether 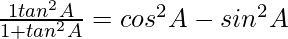\frac{1−tan^2A}{1+tan^2A} = cos^2 A - sin^2 A or not.

Solution:

Given, 3cot A = 4 or cot A = 4/3

Draw a △ ABC where ∠B = 90°, AB = 4, BC = 3

Using Pythagoras Theorem

AC2 = AB2 + BC2

AC2 = 42 + 32 = 16 + 9

AC2 = 25

AC = 5

Now, 

Taking LHS

=\frac{1−tan^2A}{1+tan^2A}

=\frac{1−(\frac{3}{4})^2}{1+(\frac{3}{4})^2}

=\frac{1−(\frac{9}{16})}{1+(\frac{9}{16})}

=\frac{(\frac{16-9}{16})}{(\frac{16+9}{16})}  

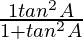
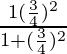
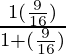
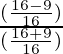
= 7/25

Taking RHS

= cos2A – sin2A

=(\frac{4}{5})^2-(\frac{3}{5})^2

=(\frac{16}{25})-(\frac{9}{25})

=(\frac{16-9}{25})

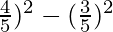
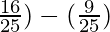
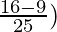
= 7/25

RHS = LHS (Hence Proved)

Question 9. If tanθ = a/b, find the value of 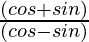\frac{(cosθ+sinθ)}{(cosθ-sinθ)}     

Solution: 

Given, tanθ = a/b

Draw a △ABC where ∠B = 90°, AB = b, BC = a

Using Pythagoras Theorem

AC2 = BC2 + AB2

AC2 = a2 + b2

AC2 = 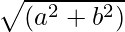\sqrt{(a^2+b^2)}

Now, 

\frac{(cosθ+sinθ)}{(cosθ-sinθ)}

=\frac{(\frac{b}{\sqrt(a^2+b^2)}+\frac{a}{\sqrt(a^2+b^2)})}{(\frac{b}{\sqrt(a^2+b^2)}-\frac{a}{\sqrt(a^2+b^2)})}

=\frac{\frac{b+a}{\sqrt(a^2+b^2)}}{\frac{b-a}{\sqrt(a^2+b^2)}}

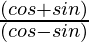
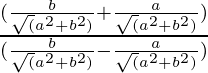
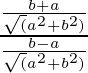
= (b + a)/(b – a)

Question 10. If 3tanθ = 4, find the value of 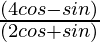\frac{(4cosθ-sinθ)}{(2cosθ+sinθ)}

Solution:

Given tanθ = 4/3 

Now, Dividing the numerator and denominator by cosθ 

=\frac{(4-tanθ)}{(2+tanθ)}

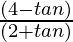
Putting the values of tanθ in the above equation

=\frac{(4-\frac{4}{3})}{(2+\frac{4}{3})}

=\frac{(\frac{16-3}{4})}{(\frac{8+3}{4})}

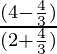
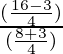
= 8/10

= 4/5

Question 11. If 3cotθ = 2, find the value of 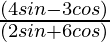\frac{(4sinθ-3cosθ)}{(2sinθ+6cosθ)}

Solution:

Given: 3cotθ = 2

  Using Pythagoras Theorem

AC2 = BC2 + AB2

AC2 = 32 + 42

AC2 = 9 + 16 = 25

AC = 5

Now, 

=\frac{(4sinθ-3cosθ)}{(2sinθ+6cosθ)}  

=\frac{(4\frac{3}{\sqrt13}-3\frac{2}{\sqrt13})}{(2\frac{3}{\sqrt13}+6\frac{2}{\sqrt13})}

=\frac{(\frac{12}{\sqrt13}-\frac{6}{\sqrt13})}{(\frac{6}{\sqrt13}+\frac{12}{\sqrt13})} 

=\frac{\frac{12-6}{\sqrt13}}{\frac{6+12}{\sqrt13}} 

=\frac{\frac{6}{\sqrt13}}{\frac{18}{\sqrt13}}

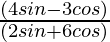
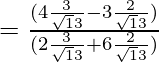
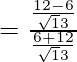
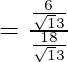
= 6/18 = 1/3 

Question 12. If tanθ = a/b, prove that 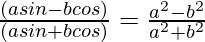\frac{(asinθ-bcosθ)}{(asinθ+bcosθ)}=\frac{a^2-b^2}{a^2+b^2}

Solution:    

Given, tanθ = a/b 

  

Using Pythagoras Theorem

AC2 = BC2 + AB2

AC2 = a2 + b2

AC2 = 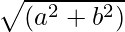\sqrt{(a^2+b^2)}

Now,   

=\frac{(asinθ-bcosθ)}{(asinθ+bcosθ)}

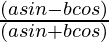
Putting the values of sinθ and cosθ in the above equation

=\frac{(a\frac{a}{\sqrt(a^2+b^2)}-b\frac{b}{\sqrt(a^2+b^2)})}{(a\frac{a}{\sqrt(a^2+b^2)}+b\frac{b}{\sqrt(a^2+b^2)})}

=\frac{(\frac{a^2}{\sqrt(a^2+b^2)}-\frac{b^2}{\sqrt(a^2+b^2)})}{(\frac{a^2}{\sqrt(a^2+b^2)}+\frac{b^2}{\sqrt(a^2+b^2)})}

=\frac{(\frac{a^2-b^2}{\sqrt(a^2+b^2)})}{(\frac{a^2+b^2}{\sqrt(a^2+b^2)})}

=\frac{a^2-b^2}{a^2+b^2}

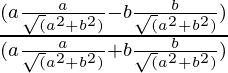
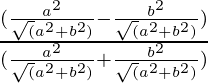
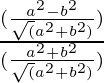
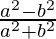
Hence Proved

Question 13. If secθ = 13/5, prove that 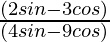\frac{(2sinθ-3cosθ)}{(4sinθ-9cosθ)}=3

Solution:  

Given, secθ = 13/5

Using Pythagoras Theorem

AC2 = BC2 + AB2

132 = BC2 + 52

BC2 = 169 – 25 = 144

BC = 12

Now,    

Taking LHS 

=\frac{(2sinθ-3cosθ)}{(4sinθ-9cosθ)}

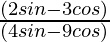
Putting the values of sinθ and cosθ in the above equation

=\frac{(2\frac{12}{13}-3\frac{5}{13})}{(4\frac{12}{13}-9\frac{5}{13})}

=\frac{(\frac{24}{13}-\frac{15}{13})}{(\frac{48}{13}-\frac{45}{13})}

=\frac{(\frac{24-15}{13})}{(\frac{48-45}{13})}

=\frac{(\frac{9}{13})}{(\frac{3}{13})}  

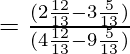
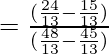
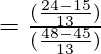
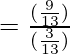
= 3 = RHS

Hence Proved

Question 14. If cosθ = 12/13, show that sinθ(1 – tanθ) = 35/156 

Solution:

We have cosθ = 12/13

Using Pythagoras Theorem

AC2 = BC2 + AB2

132 = BC2 + 122

BC2 = 169 – 144 = 25

BC = 5

Now, 

Taking LHS

= sinθ(1 – tanθ)

=\frac{5}{13}(1-\frac{5}{12})

=\frac{5}{13}.\frac{7}{12}

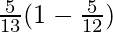
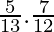
= 35/156

= RHS

Hence Proved

Question 15. If cotθ = 1/√3, show that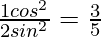\frac{1−cos^2θ}{ 2−sin^2θ}=\frac{3}{5}

Solution:

Given, cotθ = 1/√3

tanθ = 1/cotθ =√3 

From Pythagoras theorem,

AC2 = AB2 + BC2

AC2 = 12 + (√3)2

AC2 = 3 + 1 = 4

AC = 2

Now, 

Taking LHS

=\frac{1−cos^2θ}{ 2−sin^2θ}

=\frac{1-(\frac{1}{2})^2}{2-(\frac{\sqrt3}{2})^2}

=\frac{(4−1)}{(8−3)}

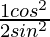
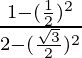
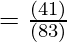
= 3/5         

Hence Proved

Question 16. If tanθ = 1/√7, then 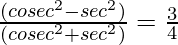\frac{(cosec^2θ-sec^2θ)}{(cosec^2θ+sec^2θ)}=\frac{3}{4}   

Solution:

We have

tanθ = 1/√7

cotθ = √7

We know sec2θ = (1 + tan2θ) = 1 + 1/7 = 8/7

and cosec2θ = (1 + cot2θ) = 1 + 7 = 8

Now, 

\frac{(cosec^2θ-sec^2θ)}{(cosec^2θ+sec^2θ)}

=\frac{(8-\frac{8}{7})}{(8+\frac{8}{7})}

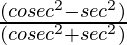
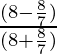
= 48/64 = 3/4

Question 17. If secθ = 5/4, find the value of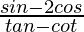\frac{sinθ-2cosθ}{tanθ-cotθ}

Solution:

Given:

secθ = 5/4

cosθ = 1/secθ = 4/5

From Pythagoras theorem,

AC2 = BC2 + AB2

52 = BC2 + 42

BC2 = 25 − 16 = 9

BC = 3

Now,

=\frac{sinθ−2cosθ}{tanθ−cotθ}=\frac{\frac{3}{5}-2(\frac{4}{5})}{\frac{3}{4}-\frac{4}{3}}

=\frac{\frac{-5}{5}}{\frac{-7}{12}}

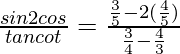
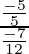
= 12/7   

Question 18. If tanθ = 12/13, find the value of 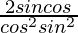\frac{2sinθcosθ}{cos^2θ−sin^2θ}

Solution:

Given: tanθ = 12/13

From Pythagoras theorem,

AC2 = BC2 + AB2

AC2 = (13)2 + (12)2

AC2 = 313

AC = √313

sinθ = 12/√313

cosθ = 13/√313

We have

\frac{2sinθcosθ}{cos^2θ−sin^2θ} = \frac{2\times\frac{12}{\sqrt{133}} \times \frac{13}{\sqrt{133}}}{(\frac{12}{\sqrt{133}})^2 - (\frac{13}{\sqrt{133}})^2 }

= \\frac{\frac{312}{313}}{\frac{169}{313}-\frac{144}{313}}

= \frac{\frac{312}{313}}{\frac{25}{313}}

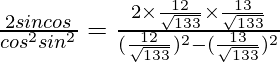
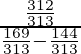
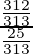
= 312/25

Question 19. If cosθ = 3/5, then evaluate 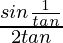\frac{sinθ−\frac{1}{tanθ}}{2tanθ}

Solution:

Given:

cosθ = 3/5

From Pythagoras theorem,

AC2 = BC2 + AB2

52 = 32 + AB2

AB2 = 25 − 9 = 16

AB = 4

Now

\frac{sinθ−\frac{1}{tanθ}}{2tanθ}

=\frac{\frac{4}{5}-\frac{1}{\frac{4}{3}}}{2\frac{4}{3}}

=\frac{\frac{4}{5}-\frac{3}{4}}{\frac{8}{3}}

=\frac{\frac{16-15}{20}}{\frac{8}{3}}

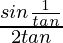
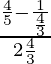
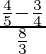
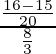
= (1/20) × (3/8)

= 3/160

Question 20. If sinθ = 3/5, then evaluate 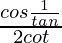\frac{cosθ−\frac{1}{tanθ}}{2cotθ}

Solution:

Given,

sinθ = 3/5

Now

\frac{sinθ−\frac{1}{tanθ}}{2cotθ}

= \frac{sinθ−{cotθ}}{2cotθ}

=\frac{cosθ−\frac{cosθ}{sinθ}}{2\frac{cosθ}{sinθ}}

=\frac{cosθ−\frac{cosθ}{sinθ}}{2\frac{cosθ}{sinθ}}

=\frac{cosθ}{cosθ}.\frac{1−\frac{1}{sinθ}}{\frac{2}{sinθ}}

=\frac{\frac{sinθ-1}{sinθ}}{\frac{2}{sinθ}}

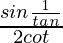
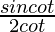
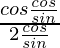
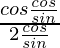
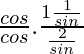
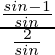
= (sinθ – 1)/(2)

Putting the value of sinθ, we get

=\frac{\frac{3}{5}-1}{2}  

=\frac{3-5}{10}

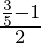
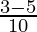
= -1/5  

Question 21. If tanθ = 24/7, find that sinθ + cosθ.

Solution:

Given:   

tanθ = 24/7 

From Pythagoras theorem,

AC2 = BC2 + AB2

AC2 = 242 + 72

AC2 = 576 + 49 = 625

AC = 25

Now, 

= sinθ + cosθ

= 24/25 + 7/25

= (24 + 7)/25

= 31/25



Like Article
Suggest improvement
Previous
Class 10 RD Sharma Solutions - Chapter 9 Arithmetic Progressions - Exercise 9.6 | Set 2
Next
Class 11 RD Sharma Solutions - Chapter 5 Trigonometric Functions - Exercise 5.1 | Set 2
Share your thoughts in the comments

Similar Reads

Class 11 RD Sharma Solutions - Chapter 7 Trigonometric Ratios of Compound Angles - Exercise 7.1 | Set 1
Class 11 RD Sharma Solutions - Chapter 9 Trigonometric Ratios of Multiple and Submultiple Angles - Exercise 9.1 | Set 2
Class 10 RD Sharma Solutions - Chapter 5 Trigonometric Ratios - Exercise 5.1 | Set 1
Class 10 RD Sharma Solutions - Chapter 5 Trigonometric Ratios - Exercise 5.1 | Set 3
Class 10 RD Sharma Solutions - Chapter 5 Trigonometric Ratios - Exercise 5.2 | Set 1
Class 10 RD Sharma Solutions - Chapter 5 Trigonometric Ratios - Exercise 5.2 | Set 2
Class 10 RD Sharma Solutions - Chapter 5 Trigonometric Ratios - Exercise 5.2 | Set 3
Class 10 RD Sharma Solutions - Chapter 5 Trigonometric Ratios - Exercise 5.3 | Set 1
Class 10 RD Sharma Solutions - Chapter 5 Trigonometric Ratios - Exercise 5.3 | Set 2
Class 11 RD Sharma Solutions - Chapter 7 Trigonometric Ratios of Compound Angles - Exercise 7.1 | Set 2

R
rahulsharma1771996
Article Tags :
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox