Class 10 RD Sharma Solutions – Chapter 4 Triangles – Exercise 4.7 | Set 2

Question 15. Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm, find the length of the other diagonal.

Solution:

Given,

In rhombus ABCD, diagonals AC and BD bisect each other at O at right angles

Each side = 10 cm and one diagonal AC = 16 cm

∴ AO = OC = 16/2 = 8 cm

Now in ∆AOB,

By using Pythagoras theorem

AB² = AO² + OB²

(10)² = (8)² + (BO)²

 100 = 64 + BO²

 BO² = 100 – 64 = 36 

BO = 6

So, BD = 2BO = 2 x 6 = 12 cm

Hence, the length of the other diagonal is 12 cm

Question 16. Calculate the height of an equilateral triangle each of whose sides measures 12 cm.

Solution:

Given,

Side of equilateral triangle=12 cm

To find: Calculate the height of an equilateral triangle

Let us draw the figure. Let us draw the altitude AD. 

BD = DC = 6cm               [ Altitude is also median of the equilateral triangle]

In ∆ADB, 

By using Pythagoras theorem

AB² = AD² + BD²                              

144 = AD² + 36

AD² = 144 − 36 = 108

AD = 10.39 cm

Hence, the height of the equilateral triangle is 10.39 cm

Question 17. In the figure, ∠B < 90° and segment AD ⊥ BC. Show that:

(i) b² = h² + a² + x² – 2ax

(ii) b² = a² + c² – 2ax

Solution:

Given : In ∆ABC, ∠B < 90°

AD ⊥ BC

AD = c, BC = a, CA = b AD = h, BD = x, DC = a – x

(i) In ∆ADC,

By using Pythagoras theorem

 AC² = AD² + DC²

 b² = h² + (a – x)²

So, b² = h² + a² + x² – 2ax

(ii) Similarly in right ∆ADB

By using Pythagoras theorem

AB² = AD² + BD²

c² = h² + x²       …..….(i)

b² = h² + a² + x² – 2ax 

= h² + x² + a² – 2ax

= c² + a² – 2ax         [From eq(i)]

So, b² = a² + c² – 2ax

Hence proved.

Question 18. In an equilateral ∆ABC, AD ⊥ BC, prove that AD² = 3 BD². 

Solution:

In right-angled ∆ABD,

By using Pythagoras theorem

AB² = AD² + BD²     ….(1)

We know that in an equilateral triangle every altitude is also median.

So, AD bisects BC.

We have BD = DC

Since ∆ABC is an equilateral triangle, AB = BC = AC

So, we can write equation (1) as

BC² = AD² + BD²       ….(2)

But BC = 2BD

Therefore, equation (2) becomes,

(2BD)² = AD² + BD²

On simplifying the equation we get,

4BD² – BD² = AD²

3BD² = AD²

So, AD² = 3BD²

Hence proved

Question 19. ∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that

(i) AB² = BC.BD

(ii) AC² = BC.DC

(iii) AD² = BD.CD

(iv) AB²/AC² = BD/DC 

Solution:

(i) In ΔADB and ΔCAB

∠DAB = ∠ACB = 90°

∠ABD = ∠CBA                       (common angle)

∠ADB = ∠CAB                      (remaining angle)

So, by AAA 

 ΔADB ~ ΔCAB     

Hence,           

AB/CB = BD/AB

⇒ AB2 = CB × BD

(ii) Let ∠CAB = y

In ΔCBA

∠CBA = 180° − 90° − y

∠CBA = 90° − y

Similarly, in ΔCAD

∠CAD = 90° − ∠CAD = 90° − y

∠CDA = 90° − ∠CAB

= 90° − y

 ∠CDA = 180° −90° − (90° − y)

∠CDA = y

Now in ΔCBA and ΔCAD,

∠CBA = ∠CAD

∠CAB = ∠CDA

∠ACB = ∠DCA = 90°

So, by AAA rule

ΔCBA ~ ΔCAD 

So, AC /DC = BC/AC

⇒ AC² = DC × BC

(iii) In ΔDCA & ΔDAB

∠DCA = ∠DAB     (both are equal to 90°)

∠CDA = ∠ADB     (common angle)

∠DAC = ∠DBA     (remaining angle)

So, by AAA rule

ΔDCA ~ ΔDAB 

so, DC/DA = DA/DB

⇒ AD² = BD × CD

(iv) From part (i) AB² = CB x BD

From part (ii) AC² = DC × BC

So, AB²/AC²= CB x BD/DC x BC

AB²/AC² = BD/DC

Hence proved

Question 20. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?

Solution:

Given,

 AC = 18m be the height of pole.

BC = 24m is the length of a guy wire and is attached to stake B.

Now,

 In △ABC

By using Pythagoras theorem

BC² = AB² + AC²

24² = AB² + 18²

AB² = 576 − 324

= 252

So, AB = 6√7 m

Hence, the stake has to be 6√7 m from base A.

Question 21. Determine whether the triangle having sides (a – 1) cm, 2 √a cm and (a + 1) cm is a right-angled triangle. 

Solution:

Given,

The sides of triangle are (a – 1) cm, 2√a and (a + 1) cm.  

Let us considered ABC be the triangle in which with the sides are  

AB = (a – 1)cm, BC = (2√ a) cm, CA = (a + 1) cm  

AB² = (a – 1)² 

By using (a – b)² = a² + b² – 2ab

= a² + 1² – 2 × a × 1      

AB² = a² + 1 -2a

BC² = (2√a)²

∴ BC = 4a

CA² = (a + 1)²

By using (a + b)² = a² + b² + 2ab

= a² + 1² + 2 × a × 1  

CA² = a²+ 1 + 2a

By using Pythagoras Theorem

AC² = AB² + BC²

On putting value of AC², AB² and BC² in the above equation,

a² + 1 + 2a = a² + 1 – 2a + 4a

a² + 1 + 2a = a² + 1 + 2a

AC² = AB² + BC²

∆ABC is right-angled ∆ at B.

Hence proved

Question 22. In an acute-angled triangle, express a median in terms of its sides.

Solution:

Given,

 In Δ ABC AD is median.

Construction: AE ⊥ BC

Now, 

∴ BD = CD = 1/2 BC ….(1)         [AD is the median]

In Δ AED,  

By using Pythagoras Theorem

AD² = AE² + DE²

⇒ AE² = AD² – DE² …..(2)

In Δ AEB,

AB² = AE² + BE²

⇒ AD² – DE² + BE²                       [From eq(2)]

= (BD + DE)² + AD² – DE²                [∴ BE = BD + DE]

BD² + DE² + 2BD x DE + AD² – DE²

= BD² + AD² + 2BD x DE

= (1/2BC)² + AD² + (2 × 1/2BC × DE)   [From eq(1)]

= (1/4BC)² + AD² + BC x DE ….(3)

In Δ AED,

By using Pythagoras Theorem

AC² = AE² + EC²

= AD² – DE² + EC²

= AD² – DE² + (DC – DE)²

= AD² – DE² + DC² + DE² – 2DC x DE

AD² + DC² – 2DC x DE

= AD² + (1/2BC)² – (2 × 1/2BC x DE)

= AD² + (1/4BC)² – BC x DE ….(4)

On adding eq(3) and (4), we get  

AB² + AC² = 1/4BC² + AD² + BC x DE + AD² + 1/4BC² – BC x DE  

= 1/2BC² + 2AD²

2(AB² + AC²) = BC² + 4AD²

2AB² + 2AC² = BC² + 4AD²

Hence Proved

Question 23. In right-angled triangle ABC in which ∠C = 90°, if D is the mid point of BC, prove that AB² = 4AD² – 3AC².

Solution:

Given :  

∠C = 90° and D is the mid-point of BC.

To prove : AB² = 4AD² – 3AC²

In ∆ ACD,  

By using Pythagoras Theorem

AD² = AC² + CD²

CD² = AD² – AC²  ……….(1)

In ∆ACB,

By using Pythagoras Theorem

AB² = AC² + BC²

AB² = AC² + (2CD)²   [D is the mid-point of BC]

AB² = AC² + 4CD²

∴ AB² = AC² + 4(AD² – AC²)    [From eq(1)]

AB² = AC² + 4AD² – 4AC²

AB² = 4AD² – 4AC² + AC²

∴ AB² = 4AD² – 3AC²

Hence Proved

Question 24. In the figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that 

(i) b² = p² + a²/4 + ax

(ii) c² = p²– ax + a²/4 

(iii) b² + c² = 2p² + a²/2

Solution:

Given,

D is the midpoint of BC

(i) In ∆ AEC

AC² = AE² + EC²

b² = AE² + (ED + DC)²

b² = AD² + DC² + 2 x ED x DC            [Given BC = 2CD]

b² = p² + (a/2)² + 2(a/2)x

b² = p² + a²/4 + ax      ………..(i)

(ii) In ∆ AEB

AB² = AE² + BE²

c² = AD² – ED² + (BD – ED)²

c² = p² – ED² + BD² + ED² – 2BD x ED

c² = P² + (a/2)² – 2(a/2)²x

c² = p² – ax + a²/4 ……………….(ii)

(iii) Adding eqn (i) and (ii) we get,

b² + c² = 2p² + a²/2

Hence Proved

Question 25. In ∆ABC, ∠A is obtuse, PB x AC and QC x AB. Prove that:

(i) AB x AQ = AC x AP

(ii) BC² = (AC x CP + AB x BQ)

Solution:

(i) Given :

∠A is obtuse.

PB is perpendicular to AC.

QC is perpendicular to AB.

To Prove :

AB × AQ = AC × AP.

Proof:

In ΔACQ and ΔABP,

⇒ ∠CAQ = ∠BAP          [Vertically opposite ∠]

⇒ ∠Q = ∠P                    [∠Q = ∠P = 90 º]

So, by AA rule

ΔACQ ~ ΔABP          

By Property of Similar Triangles,

⇒ CQ/BP = AC/AB = AQ/AP

⇒ AC/AB = AQ/AP

⇒ AB × AQ = AC × AP  ……..(i)

Hence Proved.

(ii) To Prove :

BC² = AB × BQ + AC × CP

Proof:

By using Pythagoras Theorem

⇒ BC² = CQ² + QB²

⇒ BC² = CQ² + (QA + AB)²

⇒ BC² = CQ² + QA² + AB² + 2 QA × AB

⇒ BC² = CQ² + QA² + AB² + QA × AB + QA × AB

⇒ BC² = AC² + AB² + QA × AB + QA × AB           [In ΔACQ, CQ² + QA² = AC²]

⇒ BC² = AC² + AB² + QA × AB + AC × CP            [By Eq (i)]

⇒ BC² = AC² + AC × CP + AB² + QA × AB

⇒ BC² = AC × (AC + CP) + AB × (QA + AB)

⇒ BC² = AC × CP + AB × BQ                                  [CP = AC + CP, BQ = AQ + AB]

⇒ BC² = AB × BQ + AC × CP.

Hence, Proved.

Question 26. In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC² = 4 (AD² – AC²).

Solution:

Given:

∠C = 90°

In ∆ADC

By using Pythagoras Theorem

AD² = AC² + DC²

AD² = AC² + (1/2BC)²    [DC = 1/2BC]

AD² = AC² + 1/4(BC)²

4AD² = 4AC² + (BC)²

-(BC)² = 4AC² – 4AD² 

Taking minus common

(BC)² = 4(AD² – AC²)

Hence, proved

Question 27. In a quadrilateral ABCD, ∠B = 90°, AD² = AB² + BC² + CD², prove that ∠ACD = 90°.

Solution:

Given: ABCD is a quadrilateral, ∠B = 90° and AD² = AB² + BC² + CD²

To prove: ∠ACD = 90°

Proof: In right ∆ABC,

By using Pythagoras Theorem

AC² = AB² + BC² … (1)

Given, AD² = AB² + BC² + CD²

⇒ AD² = AC² + CD²  [Using eq(1)]

In ∆ACD,

AD² = AC²+ CD²

So, ∠ACD = 90° [By converse of Pythagoras theorem]

Question 28. An aeroplane leaves an airport and flies due north at a speed of 1000 km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/ hr. How far apart will be the two planes after 1and1/2 hours?

Solution:

Given that speed of first aeroplane = 1000 km/hr

Distance travelled by first aeroplane (due north) in 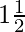 hours = 1000 x 3/2 km = 1500 km

Speed of second aeroplane = 1200 km/hr

Distance travelled by first aeroplane (due west) in 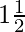 hours = 1200 × 3/2 km = 1800 km

Now in ΔAOB,

Using Pythagoras Theorem,

AB² = AO² + OB²

⇒ AB² = (1500)² + (1800)²

⇒ AB = √(2250000 + 3240000)

= √5490000

⇒ AB = 300√61 km

Hence, in 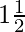 hours the distance between two plane = 300√61 km.