Class 10 RD Sharma Solutions – Chapter 4 Triangles – Exercise 4.6 | Set 2
Last Updated :
26 May, 2021
Question 11. The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
Solution:

Let us consider ∆ABC and ∆DEF, AL and DM are the medians of ∆ABC and ∆DEF
It is given that the area of ∆ABC = 121 cm2 and area of ∆DEF = 64 cm2
AL = 12.1 cm
Let us assume DM = x cm
Given that, ∆ABC ~ ∆DEF
So,
ar(∆ABC)/ar(∆DEF) = AL2/DM2
= 121/64 = (12.1)2/x2
11/8 = 12.1/x
⇒ x = (8 × 12.1)/11 = 8.8
Hence, the median of the second triangle is 8.8cm
Question 12. In ∆ABC ~ ∆DEF such that AB = 5 cm and (∆ABC) = 20 cm2 and area (∆DEF) = 45 cm2, determine DE.
Solution:

Given that,
area (∆ABC) = 20 cm²
area (∆DEF) = 45 cm²
AB = 5 cm
Let us consider DE = x cm
Also, given that ∆ABC ~ ∆DEF
ar(∆ABC)/ar(∆DEF) = AB2/DE2
⇒20/45 = (5)2/x2
⇒20/45 = 25/x2
⇒x2 = (25 × 45)/20 = 225/4 = (15/2)2
x = 15/2 = 7.5
DE = 7.5cm
Question 13. In ∆ABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divide ∆ABC into two parts equal in area. Find BP/AB.
Solution:

It is given that, in ∆ABC, PQ || BC and line PQ divide the ∆ABC into two parts
∆APQ and trap. BPQC equally
i.e., area ∆APQ = area BPQC
Now we have to find BP/AB.
As we know that PQ||BC
So, ∆APQ ∼ ∆ABC
⇒ ar.(∆APQ)/ar.(∆ABC) = AP2/AB2
⇒ ar.(∆ABC)/ar.(∆APQ) = AB2/AP2
2/1 = AB2/AP2
{area ∆APQ = area trap. BPQC
Area ∆ABC = 2area (∆APQ)}
⇒ AB/AP = √2/1
⇒√2 AP = AB = AP + PB
⇒√2AP – AP = PB
⇒(√2 – 1)AP = PB
BP/AP = (√2 – 1)/1
Question 14. The areas of two similar triangles ABC and PQR are in the ratio 9 : 16. If BC = 4.5 cm, find the length of QR.
Solution:

Given that, area (∆ABC) : area (∆PQR) = 9 : 16
∆ABC ~ ∆PQR
and BC = 4.5 cm
Let us considered QR = x cm
As we know that ∆ABC ~ ∆PQR
ar.(∆ABC)/ar.(∆PQR) = BC2/QR2 ⇒ 9/16 = (4.5)2/x2
⇒ (3/4)2 = (4.5/x)2 ⇒ 4.5/x = 3/4
x = (4.5 × 4)/3 = 60
Hence, the length of QR is 6cm
Question 15. ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 cm, prove that area of ∆APQ is one sixteenth of the area of ∆ABC.
Solution:

Given that, in ∆ABC, P and Q are two points on line AB and AC
AP = 1 cm, PB = 3 cm, AQ = 1.5 cm and QC = 4.5 cm
Now, AP/PB = 1/3 and AQ/QC = 1.5/4.5 = 1/3
In ∆APQ and ∆ABC
AP/PB = AQ/QC
PQ||BC
Hence, ∆APQ ∼ ∆ABC
So, ar.(∆APQ)/ar.(∆ABC) = AP2/PB2 = AP2/(AP + PB)2
ar.(∆APQ)/ar.(∆ABC) = 12/(1 + 3)2 = 1/16
Hence, area of ∆APQ = 1/16 of area of ∆ABC
Question 16. If D is a point on the side AB of ∆ABC such that AD : DB = 3 : 2 and E is a point on BC such that DE || AC. Find the ratio of areas of ∆ABC and ∆BDE.
Solution:

Given that in ∆ABC, D is a point on AB such that AD : DB = 3 : 2
DE||AC
In ∆BDE and ∆ABC
∠BDE = ∠A
∠DBE = ∠ABC
So, by AA, ∆BED ∼ ∆ABC
Therefore, ar.(∆ABC)/ar.(∆BDE) = AB2/BD2 = (BD + AD)2/BD2
= (2 + 3)2/22 = 52/22 = 25/4
Hence, the ratio of areas of ∆ABC and ∆BDE is 25:4
Question 17. If ∆ABC and ∆BDE are equilateral triangles, where D is the mid point of BC, find the ratio of areas of ∆ABC and ∆BDE.
Solution:

Given that ∆ABC and ∆DBE are equilateral triangles, where D is mid point of BC
So, BD = 1/2BC
Now area of ∆ABC
√3/4(side)2 = √3/4BC2
and area of ∆DBE
√3/4(side)2 = √3/4BD2
√3/4(side)2 = √3/4(1/2BC)2
√3/4(side)2 = √3/16(BC)2
So, the ratio between areas is
= area(∆ABC)/area(∆DBE) =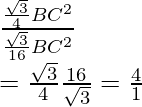
Hence, the ratio of areas of ∆ABC and ∆BDE is 4:1
Question 18. Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
Solution:
Let us consider two triangles, ∆ABC and ∆XYZ and these triangles have equal vertical angle, i.e., ∠A and ∠X
And AD and XO is the heights of these triangles.
So, ∆ABC/∆XYZ = AB/AC = XY/XZ
In ∆ABC and ∆XYZ
∠A = ∠X
AB/AC = XY/XZ
So, by SAS
∆ABC ~ ∆XYZ
So, ar(∆ABC)/ar(∆XYZ) = AD2/XO2
As we know that ar(∆ABC)/ar(∆XYZ) = 36/25
So,
36/25 = AD2/XO2
6/5 = AD/XO
Hence, the ratio of their corresponding heights is 6:5
Question 19. In the figure, ∆ABC and ∆DBC are on the same base BC. If AD and BC intersect at O, prove that 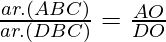
Solution:

Given that two ∆ABC and ∆DBC are on the same base BC as shown in the given figure
AC and BD intersect each other at O
Now, Draw AL ⊥ BC and DM ⊥BC
Prove: 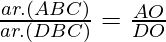
Proof:
In ∆ALO and ∆DMO,
∠L =∠M = 90°
∠AOL = ∠DOM [Vertically opposite angles]
So, by AA, ∆ALO ∼ ∆DMO
So, AL/DM = AO/DO
Now 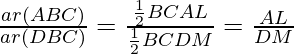
But AL/DM = AO/DO (Proved above)
So, 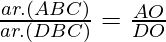
Hence proved
Question 20. ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that
(i) ∆AOB ~ ∆COD
(ii) If OA = 6 cm, OC = 8 cm, find
(a)ar(∆AOB)/ar(∆COD) (b) ar(∆AOD)/ar(∆COD)
Solution:

Given that ABCD is a trapezium in which AB || CD and the diagonals AC and BD intersect at O
Now, in the figure from point D, draw DL⊥AC
(i) In ∆AOB and ∆COD
∠AOB =∠COD [Vertically opposite angles]
∠OAB =∠OCD [Alternate angles]
So, by AA criterion
∆AOB ~ ∆COD
(ii) Given that OA = 6 cm, OC = 8 cm
As we know that ∆AOB ~ ∆COD
So, OA/OC = OB/OD = AB/CD
(a) ar(∆AOB)/ar(∆COD) = AO2/OC2
= 62/82 = 36/64 = 9/16
Therefore, ar(∆AOB)/ar(∆COD) = 9/16
(b) As we know that ∆AOD and ∆COD have their bases on the same line and their vertex A is common
Therefore, ar(∆AOD)/ar(∆COD) = AO/OC = 6/8 = 3/4
Question 21. In ∆ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ∆APQ and trapezium BPQC.
Solution:

Given that, ABC is a triangle, in which P divides the side AB such that
AP : PB = 1 : 2. Q is a point in AC such that PQ || BC
In ∆APQ and ∆ABC
∠APQ = ∠B
∠PAQ = ∠BAC
So, by AA criterion
∆APQ ∼ ∆ABC
So,
ar(∆APQ)/ar(∆ABC) = (AP)2/(AB)2
ar(∆APQ)/ar(∆ABC) = (1)2/(1 + 2)2 = (1)2/(3)2 = 1/9
9 ar(∆APQ) = ar(∆ABC)
9 ar(∆APQ) = ar(∆APQ) + ar(trap. BPQC)
9 ar(∆APQ) = ar(trap BPQC)
ar(∆APQ)/ar(trap BPQC) = 1/9
Hence, the ratio of the areas of ∆APQ and trapezium BPQC is 1:9
Question 22. AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area (∆ADE) : Area (∆ABC) = 3 : 4.
Solution:

Given that AD is an altitude of an equilateral triangle ABC.
On AD as base, another equilateral triangle ADE is constructed
Prove: Area (∆ADE) : Area (∆ABC) = 3 : 4
Proof:
Area of ∆ABC = √3/4 BC2
and AD = √3/2 BC
Area of ∆ADE = √3/4 AD2
= √3/4 (√3/2 BC)2 = 3√3/16 BC2
So, the ratio of area (∆ADE):area(∆ABC) = 3√3/16 BC2 : √3/4 BC2
= 3/4:1 = 3:4
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...