Class 10 RD Sharma Solutions – Chapter 16 Surface Areas and Volumes – Exercise 16.3 | Set 2
Last Updated :
14 Sep, 2021
Question 11. A bucket is in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm respectively. Find the capacity and surface area of the bucket. Also, find the cost of milk which can completely fill the container, at the rate of Rs.25 per litre.
Solution:
Let R and r be the radii of the top and base of the bucket respectively,
Let h be its height.
Then, we have R = 20 cm, r = 10 cm, h = 30 cm
Capacity of the bucket = Volume of the frustum of the cone
= 1/3 π(R2 + r2 + R r )h
= 1/3 π(202 + 102 + 20 x 10 ) x 30
= 3.14 x 10 (400 + 100 + 200)
= 21980 cm3 = 21.98 litres
Now,
Surface area of the bucket = CSA of the bucket + Surface area of the bottom
= π l (R + r) + πr2
We know that,
l = √h2 + (R – r)2
= √[302 + (20 – 10)2] = √(900 + 100)
= √1000 = 31.62 cm
So,
The Surface area of the bucket = (3.14) x 31.62 x (20 + 10) + (3.14) x 102
= 2978.60 + 314
= 3292.60 cm2
Next, given that the cost of 1 litre milk = Rs 25
Thus, the cost of 21.98 litres of milk = Rs (25 x 21.98) = Rs 549.50
Question 12. Radii of circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Finds its total surface area.
Solution:
Given:
Radii of top circular ends (r1) = 20 cm
Radii of bottom circular end of bucket (r2) = 12 cm
Let height of bucket be ‘h’.
Volume of frustum cone = 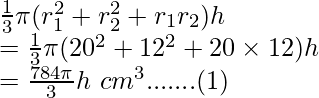
Given capacity/ volume of bucket = 12308.8 cm3 —–(2)
Equating (1) & (2)
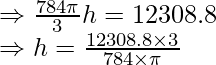
⇒ h = 15 cm
Therefore,
Height of bucket (h) = 15 cm
Let ‘l’ be slant height of bucket
⇒ l2 = (r1 – r2)2 + h2
⇒ l = 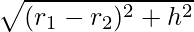
⇒ l = 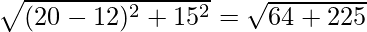
⇒ l = 17 cm
Therefore,
Length of bucket/ slant height of bucket (l) = 17 cm
Curved surface area of bucket = π(r1 + r2)l + πr22
= π(20 + 12)17 + π(12)2
= π(32)17 + π(12)2
= π(9248 + 144) = 2160.32 cm2
Therefore,
Curved surface area = 2160.32 cm2
Question 13. A bucket made of aluminium sheet is of height 20 cm and its upper and lower ends are of radius 25 cm and 10 cm. Find the cost of making a bucket if the aluminium sheet costs Rs 70 per 100 cm2?
Solution:
Given:
Height of bucket (h) = 20 cm
Upper radius of bucket (r1) = 25 cm
Lower radius of bucket (r2) = 10 cm
Let ‘l’ be slant height of bucket
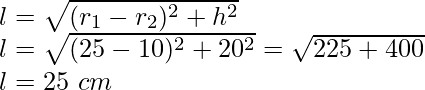
Therefore,
Slant height of bucket (l) = 25 cm
Curved surface area of bucket = π(r1 + r2)l + πr22
= π(25 + 10)25 + π(10)2
= π(35)25 + π(100) = 975π
Curved surface area = 3061.5 cm2
Cost of making bucket per 100 cm2 = Rs 70
Cost of making bucket per 3061.5 cm2 = 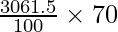
= Rs 2143.05
Therefore,
Total cost for 3061.5 cm2 = Rs 2143.05
Question 14. Radii of circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area?
Solution:
Given:
Slant height of frustum cone = 10 cm
Radii of circular ends of frustum cone are 33 and 27
r1 = 33 cm; r2 = 27 cm
Total surface area of a solid frustum of cone = π(r1 + r2) × l + πr12 + πr22
= π(33 + 27) × 10 + π(33)2 + π(27)2
= π(60) × 10 + π(33)2 + π(27)2
= π(600 + 1089 + 729)
= 2418π cm2
= 7599.42 cm2
Therefore,
Total surface area of frustum cone = 7599.42 cm2
Question 15. A bucket made up of a metal sheet is in form of a frustum of cone of height 16 cm with diameter of its lower and upper ends as 16 cm and 40 cm. Find the volume of bucket, Also find cost of bucket if the cost of metal sheet used is Rs 20 per 100 cm2?
Solution:
Given:
Height of frustum cone = 16 cm
Diameter of lower end of bucket (d1) = 16 cm
Lower end radius (r1) = 16/2 = 8 cm
Upper end radius (r2) = 40/2 = 20 cm
Let ‘l’ be slant height of frustum of cone
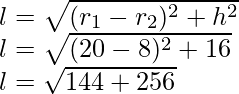
l = 20 cm
Therefore,
Slant height of frustum cone (l) = 20 cm
Volume of frustum cone =

Volume = 10449.92 cm3
Curved surface area of frustum cone = π(r1 + r2)l + πr22
= π(20 + 8)20 + π(8)2
= π(560 + 64) = 624π cm2
Cost of metal sheet per 100 cm2 = Rs 20
Cost of metal sheet for 624π cm2 = 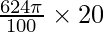
= Rs 391.90
Therefore,
Total cost of bucket = Rs 391.9
Question 16. A solid is in the shape of a frustum of a cone. The diameters of two circular ends are 60 cm and 36 cm and height is 9 cm. Find area of its whole surface and volume?
Solution:
Given:
Height of a frustum cone = 9 cm
Lower end radius (r1) = 60/2 cm = 30 cm
Upper end radius (r2) = 36/2 cm = 18 cm
Let slant height of frustum cone be l

Volume of frustum cone =
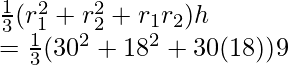
= 5292π cm3
Volume = 5292π cm3
Total surface area of frustum cone = π(r1 + r2) × l + πr12 + πr22
= π(30 + 18)15 + π(30)2 + π(18)2
= π(48(15) + (30)2 + (18)2)
= π(720 + 900 + 324)
= 1944π cm2
Therefore,
Total surface area = 1944π cm2
Question 17. A milk container is made of metal sheet in the shape of frustum of a cone whose volume is 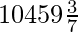 cm3. The radii of its lower and upper circular end are 8 cm and 20 cm. Find the cost of metal sheet used in making container at rate of Rs 1.40 per cm2?
cm3. The radii of its lower and upper circular end are 8 cm and 20 cm. Find the cost of metal sheet used in making container at rate of Rs 1.40 per cm2?
Solution:
Given:
Lower end radius of bucket (r1) = 8 cm
Upper end radius of bucket (r2) = 20 cm
Let height of bucket be ‘h’
V1 = 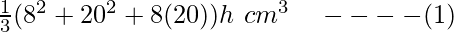
Volume of milk container = 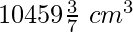
V2 = 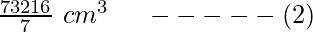
Equating (1) and (2)
V1 = V2
⇒ 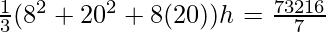
⇒ h = 
⇒ h = 16 cm
Therefore,
Height of frustum cone(h) = 16 cm
Let slant height of frustum cone be ‘l’
l = 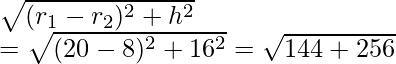
l = 20 cm
Therefore,
Slant height of frustum cone (l) = 20 cm
Total surface area of frustum cone = π(r1 + r2)l + πr12 + πr22
= π(20 + 8)20 + π(20)2 + π(8)2
= π(560 + 400 + 64)
= π(960 + 64) = 1024π = 3216.99 cm2
Total surface area = 3216.99 cm2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...