Class 10 RD Sharma Solutions – Chapter 16 Surface Areas and Volumes – Exercise 16.3 | Set 1
Last Updated :
18 Mar, 2021
Question 1. A bucket has top and bottom diameters of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs 1.20 per dm2.
Solution:
Given,
Diameter of the top of the bucket = 40 cm
Therefore,
Radius (r1) = 40/2 = 20 cm
Also,
Diameter of bottom part of the bucket = 20 cm
Therefore,
Radius (r2) = 30/2 = 10cm
Depth of the bucket (h) = 12 cm
Now,
Volume of the bucket = 1/3 π(r22 + r12 + r1 r2)h
= π/3(202 + 102 + 20 × 10)12
= 8800 cm3
Now,
Let us assume L to be the slant height of the bucket.
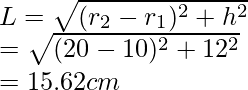
Also,
Total surface area of bucket =
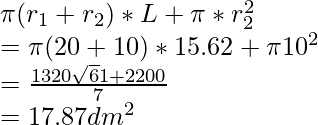
Since,
The cost of tin sheet used for making bucket per dm2 = Rs 1.20
Therefore, the total cost for making bucket 17.87dm2 = 1.20 × 17.87 = Rs 21.40
Question 2. A frustum of a right circular cone has a diameter of base 20 cm, of top 12 cm and height 3 cm. Find the area of its whole surface and volume.
Solution:
Given,
We know,
Base diameter of the cone (d1) = 20 cm
Therefore,
Radius (r1) = 20/2 cm = 10 cm
Top diameter of Cone (d2) = 12 cm
Therefore,
Radius (r2) = 12/2 cm = 6 cm
Also,
Height of the cone (h) = 3 cm
Volume of the frustum of a right circular cone = 1/3 π(r22 + r12 + r1 r2 )h
Substituting the values,
= π/3(102 + 62 + 10 × 6)3
= 616 cm3
Let us assume ‘L’ to be the slant height of the cone, then we know that
Now,
L = √(r1 – r21)2 + h2
L = √(10 – 6)2 + 32
L = √(16 + 9)
Solving, we get,
L = 5cm
Therefore,
The slant height of cone (L) = 5 cm
Thus,
Total surface area of the frustum = π(r1 + r2) x L + π r12 + π r22
Substituting the values,
= π(10 + 6) × 5 + π × 102 + π × 62
= π(80 + 100 + 36)
= π(216)
= 678.85 cm2
Question 3. The slant height of the frustum of a cone is 4 cm and the perimeters of its circular ends are 18 cm and 6 cm. Find the curved surface of the frustum.
Solution:
Given,
Slant height of frustum of the cone (l) = 4 cm
Let us assume the ratio of the top and bottom circles be r1 and r2 respectively.
And, we know,
Perimeters of the circular ends are 18 cm and 6 cm respectively.
Substituting the values,
⟹ 2πr1 = 18 cm and 2πr2 = 6 cm
Solving, we get,
⟹ πr1= 9 cm and πr2 = 3 cm
Since, we know,
Curved surface area of frustum of a cone = π(r1 + r2)l
= (πr1+πr2)l
= (9 + 3) × 4
= (12) × 4 = 48 cm2
Therefore, the curved surface area = 48 cm2
Question 4. The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
Solution:
Given values,
Perimeter of the upper end of the circular cone= 44 cm
Now,
2 π r1 = 44
2(22/7) r1 = 44
Solving, we get,
r1 = 7 cm
Also,
Perimeter of the lower end of the circular cone= 33 cm
2 π r2 = 33
2(22/7) r2 = 33
Solving,
r2 = 21/4 cm
Now,
Let us assume the slant height of the frustum of a right circular cone to be L
Given,
L = 16.1 cm
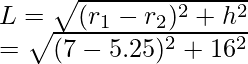
We know, the curved surface area of the frustum cone = π(r1 + r2)l
Substituting values,
= π(7 + 5.25)16.1
Curved surface area of the frustum cone = 619.65 cm3
And, The volume of the frustum cone = 1/3 π(r22 + r12 + r1 r2)h
= 1/3 π(72 + 5.252 + (7) (5.25)) x 16
= 1898.56 cm3
Now, the total surface area of the frustum cone
= π(r1 + r2) x L + π r12 + π r22
= π(7 + 5.25) × 16.1 + π72 + π5.252
= π(7 + 5.25) × 16.1 + π(72 + 5.252) = 860.27 cm2
Therefore, the total surface area of the frustum cone is 860.27 cm2
Question 5. If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket.
Solution:
Given,
The height of the conical bucket = 45 cm
Also,
The radii of the two ends of the conical bucket are 28 cm and 7 cm respectively.
Now, x = 28 cm and y = 7 cm
Now, Volume of the conical bucket = 1/3 π(x2 + y2 + xy )h
Substituting the values, we get,
= 1/3 π(282 + 72 + 28 × 7)45 = 15435π
Therefore, the volume of the bucket is 48510 cm3.
Question 6. The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be 1/125 of the volume of the original cone, determine at what height above the base the section is made.
Solution:

Let the radius of the small cone and big cone be R and r cm respectively.
Given, height of the big cone = 20 cm
Let us assume the height of section made to be h cm
Now,
Calculating the height of small cone = (20 – h) cm
Considering △OAB and △OCD
∠AOB = ∠COD [common]
And, since both of the angles are 90o
∠OAB = ∠OCD
Now, by AA similarity
Then, OAB ~ △OCD
So, by C.P.S.T we have
OA/ OC = AB/ CD
Substituting values,
(20 – h)/ 20 = r/ R …… (i)
And,
Volume of small cone = 1/125 x volume of big cone, that is,
1/3 π r2(20 – h) = 1/125 × 1/3 πR2 x 20
=>r2/ R2 = 1/125 × 20/ (20 – h) [From (i)]
=>(20 – h)2/ 202 = 1/125 × 20/20 – h
=>(20 – h)3 = 203/ 125
=>20 – h = 20/5
=>20 – h = 4
Now,
h = 20 – 4 = 16 cm
Therefore, the section was made at a height of 16 cm above the base.
Question 7. If the radii of the circular ends of a bucket 24 cm high are 5 and 15 cm respectively, find the surface area of the bucket.
Solution:
We know,
Height of the bucket (h) = 24 cm
Radii of the circular ends of the bucket x and y are 5 cm and 15 cm respectively.
Let us assume L to be the slant height of the bucket
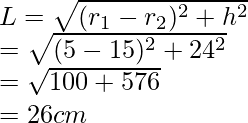
Now,
Curved surface area of the bucket is given by= π(x+ y)l + πx2
Substituting the values, we get,
= π(5 + 15)26 + π52 = π(520 + 25) = 545π cm2
Question 8. The radii of circular bases of a frustum of a right circular cone are 12 cm and 3 cm and the height is 12 cm. Find the total surface area and volume of frustum.
Solution:
Given,
Height of frustum cone = 12 cm
Now,
The radius of the lower end (x) of the frustum of cone= 12 cm
The radius of the upper end (y) of the frustum of cone= 3 cm
Let us assume L to be the slant height of the frustum cone
Now,

L = 15 cm
Now,
The total surface area of frustum of a cone = π (x + y) x L + π x2 + π y2
Substituting values,
= π (12 + 3)15 + π122 + π32
Solving, we get,
= 378 π cm2
Also,
Volume of frustum cone = 1/3 π(y2 + x2 + x y )h
= 1/3 π(122 + 32 + 12 × 3) × 12
= 756π cm3
Question 9. A tent consists of a frustum of a cone capped by a cone. If radii of the ends of the frustum be 13 m and 7 m, the height of frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent.
Solution:
Given,
Radii of the frustum cone are 13 cm and 7 cm respectively.
Height of the frustum cone, h = 8 m
Now,
The radius of the lower end (x) of the frustum of cone= 13 cm
The radius of the upper end (y) of the frustum of cone= 7 cm
Let us assume L to be the slant height of the frustum cone
Now,
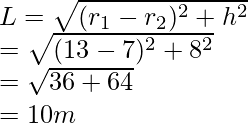
Curved surface area of the frustum (s1) = π(x + y) × L
= π(13 + 7) × 10
= 200 π m2
Also,
Slant height of conical cap = 12 m
And,
Base radius of upper cap cone = 7 m
Now,
The curved surface area of upper cap cone (s2) = π *r *l
= π × 7 × 12
= 264 m2
Therefore, the total canvas required for tent (S)
= Curved surface area of the frustum + Curved surface area of upper cap cone
= s1 + s2
S = 200π + 264
= 892.57 m2 which is the canvas required for the tent
Question 10. A milk container of height 16 cm is made of metal sheet in the form of frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of Rs. 44 per litre which the container can hold.
Solution:
Given,
The radius of the lower end (x) of the frustum of cone= 8 cm
The radius of the upper end (y) of the frustum of cone= 20 cm
Height, h = 16 cm
Now,
The capacity of the container = Volume of frustum of the cone
which is equivalent to,
= 1/3 π(y2 + x2 + xy )h
Substituting the values,
= 1/3 π(202 + 82 + (20) (8) ) x 16
= 10459.42 cm3 = 10.46 litres
Cost of 1 litre of milk = Rs 44
Cost of 10.46 litres of milk = Rs (44 x 10.46) = Rs 460.24
Therefore,
The cost of 21.98 litres of milk = Rs (25 x 21.98) = Rs 549.50
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...