Class 10 RD Sharma Solutions – Chapter 16 Surface Areas and Volumes – Exercise 16.2 | Set 3

Question 25. A hemispherical depression is cut from one face of a cubical wooden block of the edge 21 cm such that the diameter of the hemispherical surface is equal to the edge of the cubical surface. Determine the volume and the total surface area of the remaining block.

Solution: 

According to the question 

Edge of the cubical wooden block (e) = 21 cm,

Diameter of the hemisphere = Edge of the cubical wooden block = 21 cm,

So, the radius of the hemisphere (r) = 10.5 cm

Now, we find the volume of the remaining block 

V = volume of the cubical block – volume of the hemisphere

V = e³ − (2/3 πr³)

=  21³ − (2/3 π10.5³) = 6835.5 cm³

Now, we find the surface area of the block 

A_S = 6(e²) = 6(21²)          

Now, we find the curved surface area of the hemisphere 

A_C = 2πr² = 2π10.5²

The base area of the hemisphere is

A_B = πr² = π10.5²

So, the remaining surface area of the box 

= A_S – (A_C + A_B)

= 6(21²) – (2π10.5² + π10.5²) = 2992.5 cm²

Hence, the remaining surface area of the block is 2992.5 cm² and the volume is 6835.5 cm³

Question 26. A boy is playing with a toy which is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21 cm and its volume is 2/3 of the volume of the hemisphere. Calculate the height of the cone and surface area of the toy.

Solution:

According to the question 

Radius of the cone (R) = 21 cm,

Radius of the hemisphere = Radius of the cone = r = 21 cm,

Now, we find the volume of the cone 

V1 = 1/3 × πR²L

Here, L is the slant height of the cone

= 1/3 × π21²L

Now, we find the volume of the Hemisphere 

V2 = 2/3 × πR³

= 2/3 × π x 21³ = 169714.286 cm³

Since, volume of the cone = 2/3 of the hemisphere,       

So,

V1 = 2/3 V2

V1 = 2/3 ×169714.286

1/3 × π x 21² x L = 2/3×π x 21³

L = 28 cm

So, the height of the cone is 28 cm

Now, we find the curved surface area of the cone 

A1 = πRL

A1 = π × 21 × 28 cm²

Now, we find the curved surface area of the hemisphere 

A2 = 2πR²

A2 = 2π(21²) cm²

Hence, the total surface area of the toy 

A = A1 + A2

= π × 21 × 28 + 2π(21²)

= 5082 cm²

Hence, the curved surface area of the toy is 5082 cm²

Question 27. Consider a solid which is in the form of a cone surmounted on hemisphere. The radius of each of them is being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the solid.

Solution:

According to the question 

Radius of the cone = Radius of the hemisphere = R = 3.5 cm,

Total height of the solid (H) = 9.5 cm,

Slant height of the cone = H – R

L = 9.5 – 3.5 = 6 cm

Now, we find the volume of the cone 

V1 = 1/3 × πR²L

= 1/3 × π x 3.5² x 6 cm³

Now, we find the volume of the hemisphere 

V2 = 2/3 × πR³

= 2/3 × π5³ cm³                  —————(ii)

Hence, the total volume of the solid is 

V = V1 + V2

= 1/3 × π x 3.5² x 6 + 2/3 × π x 5³

= 166.75 cm³

Hence, the volume of the solid is 166.75 cm³

Question 28. A wooden toy is made by scooping out a hemisphere of same radius from each end of the solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the volume of the wood in the toy.

Solution: 

According to the question 

Radius of the cylinder = Radius of the hemisphere (r) = 3.5 cm 

Height of the hemisphere (h) = 10 cm

Now, we find the volume of the cylinder 

V1 = π × r² × h 

= π × 3.5² × 10        

Now, we find the volume of the hemisphere 

V2 = 2/3 × πr³

= 2/3 × π x 3.5³ cm³

Hence, the volume of the wood in the toy is 

V = V1 – 2(V2)

= π × 3.5² × 10 – 2(2/3 × π x 3.5³)

= 205.33 cm³

Hence, the volume of the wood in the toy is 205.33 cm³

Question 29. The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the volume of the wood left.

Solution: 

According to the question 

Diameter of the wooden solid = 7 cm,

Radius of the wooden solid = 3.5 cm,

Now, we find the volume of the cube 

V1 = a³,

= 3.5³

Now, we find the volume of sphere 

V2 = 4/3 × π × r³

= 4/3 × π × 3.5³

Hence, the volume of the wood left 

V = V1 + V2

= 3.5³ − 4/3 × π × 3.5³

= 163.33 cm³

Hence, the volume of the wood left is 163.33 cm³

Question 30. From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.

Solution: 

According to the question 

Height of the cylinder = Height of the cone = H = 2.8 cm

Diameter of the cylinder = 4.2 cm,

So, the radius of the cylinder = Radius of the cone = R = 2.1 cm 

Now, we find the curved surface area of the cylindrical part 

A1 = 2πRH

= 2π(2.8)(2.1) cm²

Now, we find the curved surface area the cone = πRL

A2 = π × 2.1 × 2.8 cm²

The area of the cylindrical base = AB = πr² = π(2.1)²

Hence, the total surface area of the remaining solid is

A = A1 + A2 + AB 

= 2π(2.8)(2.1) + π × 2.1 × 2.8 + π(2.1)²

= 36.96 + 23.1 + 13.86

= 73.92 cm²

Hence, the total surface area of the remaining solid is 73.92 cm²

Question 31. The largest cone is carved out from one face of the solid cube of side 21 cm. Find the volume of the remaining solid.

Solution: 

According to the question 

Diameter of the cone = 21 cm,

So, the radius of the cone = 10.5 cm,

The height of the cone is equal to the side of the cone,

Now, we find the volume of the cube

V1 = e³

= 10.5³

Now, we find the volume of the cone 

V2 = 1/3 × πr²L

= 1/3 × π10.5221 cm³

Hence, the volume of the remaining solid 

V = V1 – V2

= 10.53 – 1/3 × π x 10.5² x 21

= 6835.5 cm³

Hence, the volume of the remaining solid is 6835.5 cm³

Question 32. A solid wooden toy is in the form of a hemisphere surmounted by a cone of the same radius. The radius of the hemisphere is 3.5 cm and the total wood used in the making of toy is 166 5⁄6 cm³. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of Rs. 10 per square cm.

Solution: 

According to the question 

Radius of the hemisphere = 3.5 cm,

Volume of the solid wooden toy = 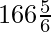 cm³,

Hence, the volume of the solid wooden toy = volume of the cone + volume of the hemisphere 

1/3 × πr²L + 2/3 × πr³ = 10016

1/3 × π3.5²L + 2/3 × π3.5³ = 10016

L + 7 = 13

L = 6 cm

Height of the solid wooden toy = Height of the cone + Radius of the hemisphere

= 6 + 3.5 = 9.5 cm

Now, we find the curved surface area of the hemisphere 

A = 2πR²

= 2π(3.5²) = 77 cm²

Cost of painting the hemispherical part of the toy = 10 x 77 = Rs. 770

Hence, the cost of painting the hemispherical part of the toy is 770 rupees

Question 33. How many spherical bullets can be made out of a solid cube of lead whose edge measures 55 cm and each of the bullet being 4 cm in diameter?

Solution:

According to the question 

Diameter of the bullet = 4 cm,

Radius of the spherical bullet = 2 cm 

So, the volume of a spherical bullet is 

V = 4/3 × π × r³

=  4/3 × π × 2³

= 4/3 × 22/7 × 2³ = 33.5238 cm³

Let’s assume that the total number of bullets be a.

So, the volume of ‘a’ number of the spherical bullets 

V1 = V x a

= (33.5238 a) cm³

and the Volume of the solid cube = (55)³ = 166375 cm³

Now, we find the volume of ‘a’ number of the spherical bullets = Volume of the solid cube

33.5238 a = 166375

a = 4962.892

Hence, the total number of the spherical bullets is 4963

Question 34. Consider a children’s toy which is in the form of a cone at the top having a radius of 5 cm mounted on a hemisphere which is the base of the toy having the same radius. The total height of the toy is 20 cm. Find the total surface area of the toy.

Solution: 

According to the question 

Radius of the conical portion of the toy (r) = 5 cm,

Total height of the toy (h) = 20 cm,

Length of the cone = L = 20 – 5 = 15 cm,

Now, we find the curved surface area of the cone 

A1 = πrL 

= π(5)(15) = 235.7142 cm²

Now, we find the curved surface area of the hemisphere 

A2 = 2πr²

= 2π(5)² = 157.1428 cm²

Therefore, The total surface area of the toy is 

A = A1 + A2

= 235.7142 + 157.1428

= 392.857 cm²

Hence, the total surface area of the children’s toy is 392.857 cm²

Question 35. A boy is playing with a toy conical in shape and is surmounted with hemispherical surface. Consider a cylinder in with the toy is inserted. The diameter of cone is the same as that of the radius of cylinder and hemispherical portion of the toy which is 8 cm. The height of the cylinder is 6 cm and the height of the conical portion of the toy is 3 cm. Assume a condition in which the boy’s toy is inserted in the cylinder, then find the volume of the cylinder left vacant after insertion of the toy.

Solution: 

According to the question 

Diameter of the cone = Diameter of the Cylinder = Diameter of the Hemisphere = 8 cm,

So, Radius of the cone = Radius of the cylinder = Radius of the Hemisphere = r = 4 cm

Height of the conical portion (L) = 3 cm,

Height of the cylinder (H) = 6 cm,

Now, we find the volume of the cylinder 

V1 = π × r² × H 

= π × 4² × 6 = 301.7142 cm³

Now, we find the vcolume of the Conical part of the toy 

V2 = 1/3 × πr²L

= 1/3 × π4² × 3 = 50.2857 cm³

Now, we find the volume of the hemispherical part of the toy 

V3 = 2/3 × πr³

= 2/3 × π4³ = 134.0952 cm³

Hence, the remaining volume the cylinder left vacant after insertion of the toy is

V = V1 – (V2 + V3)

= 301.7142 – (50.2857 + 134.0952) = 301.7142 – 184.3809

= 117.3333 cm³

Hence, the remaining volume the cylinder left vacant after insertion of the toy is 117.3333 cm3

Question 36. Consider a solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm, is placed upright in the right circular cylinder full of water such that it touches bottoms. Find the volume of the water left in the cylinder, if radius of the cylinder is 60 cm and its height is 180 cm.

Solution: 

According to the question 

Radius of the circular cone (r) = 60 cm,

Height of the circular cone (L) = 120 cm,

Radius of the hemisphere (r) = 60 cm,

Radius of the cylinder (R) = 60 cm,

Height of the cylinder (H) = 180 cm,

Now, we find the volume of the circular cone 

V1 = 1/3 × πr²L

= 1/3 × π60² × 120

= 452571.429 cm³

Now, we find the volume of the hemisphere 

V2 = 2/3 × πr³

= 2/3 × π60³ = 452571.429 cm³

Now, we find the volume of the cylinder 

V3 = π × R² × H

= π × 60² × 180 = 2036571.43 cm³

Hence, the volume of water left in the cylinder is

V = V3 – (V1 + V2)

= 2036571.43 – (452571.429 + 452571.429)

= 2036571.43 – 905142.858 = 1131428.57 cm³

= 1.1314 m³

Hence, the volume of the water left in the cylinder is 1.1314 m³

Question 37. Consider a cylindrical vessel with internal diameter 20 cm and height 12 cm is full of water. A solid cone of base diameter 8 cm and height 7 cm is completely immersed in water. Find the value of water when

(i) Displaced out of the cylinder

(ii) Left in the cylinder

Solution: 

According to the question 

Internal diameter of the cylindrical vessel = 20 cm,

So, the radius of the cylindrical vessel (r) = 10 cm 

Height of the cylindrical vessel (h) = 12 cm,

Base diameter of the solid cone = 8 cm,

So, the radius of the solid cone (R) = 4 cm 

Height of the cone (L) = 7 cm,

(i) Now, we find the volume of water displaced out from the cylinder which is equal to the volume of the cone 

V1 = 1/3 × πR²L

= 1/3 × π4² × 7 = 117.3333 cm³

Hence, the volume of the water displaced out of the cylinder is 117.3333 cm³

(ii) The volume of the cylindrical vessel is

V2 = π × r² × h

= π × 102 × 12 = 3771.4286 cm³

Hence, the volume of the water left in the cylinder is

V = V2 – V1

= 3771.4286 – 117.3333 = 3654.0953 cm³

Hence, the volume of the water left in cylinder is 3654.0953 cm³