Question 41. Three consecutive vertices of a parallelogram are (-2, -1), (1, 0) and (4, 3). Find the fourth vertex.
Solution:
Let the coordinates of three vertices are A (-2, -1), B (1, 0), and C (4, 3)
And let the diagonals AC and BD bisect each other at O

As O is the mid-point of AC
Therefore,
Vertices of O will be
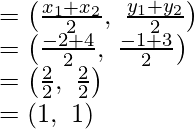
Assume coordinates of the forth vertex D be (x, y)
As O is the mid-point of BD
Thus, coordinates of O will be
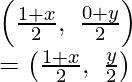
Therefore(1 + x)/2 = 1
1 + x = 2
x = 1
and
y/2 = 1
y = 2
Hence, the co-ordinates of D will be (1, 2).
Question 42. The points (3, -4) and (-6, 2) are the extremities of a diagonal of a parallelogram. If the third vertex is (-1, -3). Find the co-ordinates of the fourth vertex.
Solution:
Assume the edges of a diagonal AC of a parallelogram ABCD are A (3, -4) and C (-6, 2)
Consider AC and BD bisect each other at O.

Therefore,
Mid-point of AC will be
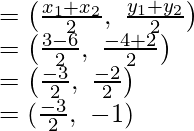
Assume the fourth vertex of the parallelogram be (x, y)
Therefore,
Mid-point of BD will be
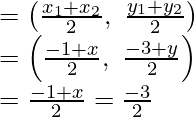
-1 + x = -3
x = -2
and
(-3 + y)/2 = -1
-3 + y = -2
y = -2 + 3 = 1
Hence, the coordinates of D are (-2, 1).
Question 43. If the co-ordinates of the mid-points of the sides of a triangle are (1, 1), (2, -3), and (3, 4), find the vertices of the triangle.
Solution:
Assume A (x1, y1), B (x2, y2) and C (x3, y3) be the vertices of the ∆ABC
D, E and F are the mid-points of BC, CA and AB respectively such that their co-ordinates are D (1, 1), E (2, -3) and F (3, 4)
D is mid-point of BC

Therefore,
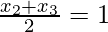
x2 + x3 = 2
and
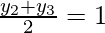
y2 + y3 = 2
Similarly, E is the mid-point of AC
Therefore,
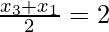
x3 + x1 = 4
and
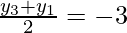
y3 + y1 = -6
And
F is the mid-point of AB
Therefore,
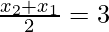
x2 + x1 = 6
and
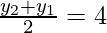
y2 + y1 = 8
Now,
x1 + x2 = 6 …………..(i)
x2 + x3 = 2 ……………(ii)
x3 + x1 = 4 …………….(iii)
On adding we will get
2(x1 + x2 + x3) = 12
x1 + x2 + x3 = 6 …………(iv)
On subtracting (ii), (iii) and (i) from (iv), we get
x1 = 4, x2 = 2, x3 = 0
Similarly
y1 + y2 = 8 ……….(v)
y2 + y3 = 2 ……….(vi)
y3 + y1 = -6 ………(vii)
On adding we will get
2(y1 + y2 + y3) = 4
y1 + y2 + y3 = 2 ………(viii)
On subtracting (vi), (vii) and (v) from (viii), we get
y1 = 0
y2 = 8
y3 = -6
Hence, the vertices of ∆ABC are A (4, 0), B(2, 8), C(0, -6)
Question 44. Determine the ratio in which the straight line x – y – 2 = 0 divides the line segment joining (3, -1) and (8, 9).
Solution:
Assume the straight line x – y – 2 = 0 divides the line segment joining the points (3, -1), (8, 9) in the ratio m : n
Co-ordinates of the point will be
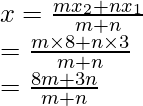
and
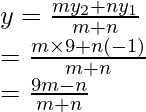
This point (x, y) lies on the line on the line x – y – 2 = 0
⇒ (8m + 3n) – (9m – n) – 2(m + n) = 0
⇒ 8m + 3n – 9m + n – 2m – 2n = 0
⇒ -3m + 2n = 0
⇒ 2n = 3m
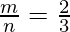
Hence, the ratio = 2 : 3 internally
Question 45. Three vertices of a parallelogram are (a + b, a – b), (2 a + b, 2a – b), (a – b, a + b). Find the fourth vertex.
Solution:
In parallelogram ABCD co-ordinates are of A (a + b, a – b), B (2a + b, 2a – b), C (a – b, a + b)
Assume coordinates of D be (x, y)
Join diagonal AC and BD
Which bisect each other at O
O is the mid-point of AC as well as BD

If O is the mid-point of AC, Then its coordinates will be
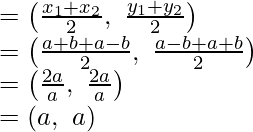
and
If O is mid-point of BD, then coordinates will be
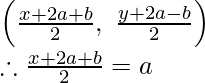
x + 2a + b = 2a
x = 2a – 2a – b = -b
and
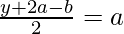
y + 2a – b = 2a
y = 2a – 2a + b = b
Hence, the coordinates of D will be (-b, b).
Question 46. If two vertices of a parallelogram are (3, 2), (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
Solution:
Two vertices of a parallelogram ABCD are A (3,2), and B (-1, 0) and its diagonals bisect each other at O (2, -5)

Assume the coordinates of C be (x1, y1) and of D be (x2, y2)
If O is the mid-point of AC, then
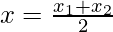
3 + x1 = 4
x1 = 4 – 3 = 1
and
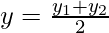
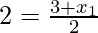
and
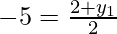
2 + y1 = -10
y1 = -10 – 2 = -12
Therefore, the coordinates of C will be (1, -12)
Again if O is mid-point of BD then
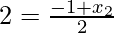
-1 + x2 = 4
x2 = 4 + 1 = 5
and
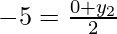
y2 = -10
Hence, the coordinates of D will be (5, -10).
Question 47. If the coordinates of the mid-points of the sides of a triangle ar6 (3, 4), (4, 6), and (5, 7), find its vertices.
Solution:
The coordinates of the mid-points of the sides BC, CA and AB are D (3, 4), E (4, 6) and F (5, 7) of the ∆ABC.

Assume the coordinates of the vertices of the triangle be A (x,1 y1), B (x2, y2), and C (x3, y3).
Now the coordinates of D will be
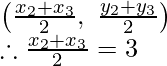
x2 + x3 = 6
and
y2 + y3 = 4
y2 + y3 = 8
Similarly, the coordinates of E will be
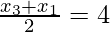
x3 + x1 = 8
and
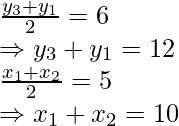
and
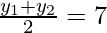
y1 + y2 = 14
Now,
x2 + x3 = 6 …….(i)
x3 + x1 = 8 ……..(ii)
x1 + x2 = 10 ……..(iii)
On adding we will get
2(x1 + x2 + x3) = 24
⇒ x1 + x2 + x3 = 24/2 = 12 ………..(iv)
On subtracting each from (iv),
We will get
x1 = 6, x2 = 4 and x3 = 2
Similarly,
y2 + y3 = 8 ……..(v)
y3 + y1 = 12 ………(vi)
y1 + y2 = 14 ……..(vii)
On Adding, we will get
2(y1 + y2 + y3) = 34
⇒ y1 + y2 + y3 = 34/2 = 17 ……..(viii)
On subtracting each from (viii),
We will get
y1 = 9
y2 = 5
y3 = 3
Hence, the coordinates will be of A (6, 9), B (4, 5) and C (2, 3)
Question 48. The line segment joining the points P (3, 3) and Q (6, -6) is trisected at the points A and B such that A is nearer to P. If A also lies on the line given by 2x+ y + k =0, find the value of k.
Solution:
Two points A and B trisect the line segment joining the points P (3, 3) and Q (6, -6) and A is nearer to P and A lies also on the line 2x + y + k = 0

Now,
A divides the line segment PQ in the ratio of 1 : 2
i.e.,
PA = AQ = 1 : 2
Assume coordinates of A be (x, y), then
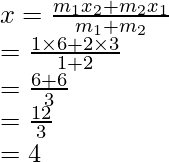
and
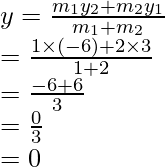
Therefore,
Coordinates of A are (4, 0)
As A lies on the line 2x + y + k = 0
Hence,
It will satisfy it
2 × 4 + 0 + k = 0
8 + k = 0
k = -8
Question 49. If three consecutive vertices of a parallelogram are (1, -2), (3, 6), and (5, 10), find its fourth vertex.
Solution:
A (1, -2), B (3, 6) and C (5, 10) are the three consecutive vertices of the parallelogram ABCD
Assume (x, y) be its fourth vertex
AC and BD are its diagonals which bisect each other at O

As O is the mid-point of AC
Therefore,
Coordinates of O will be
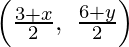
On comparing,
3 + x = 3
3 + x = 6
x = 3
and
(6 + y)/2 = 4
6 + y = 8
y = 2
Hence, the coordinates of fourth vertex D are (3, 2).
Question 50. If the points A (a, -11), B (5, b), C (2, 15), and D (1, 1) are the vertices of a parallelogram ABCD, find the values of a and b.
Solution:
A (a, -11), B (5, b), C (2, 15) and D (1, 1) are the vertices of a parallelogram ABCD
Diagonals AC and BD bisect each other at O

As O is the mid-point of AC
Therefore,
Coordinates of O will be
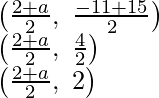
Similarly, O is the mid-point of BD also
Therefore,
Coordinates of O will be
(2 + a)/2 = 3
b + 1 = 4
b = 3
Hence,
a = 4
b = 3
Question 51. If the co-ordinates of the mid-points of the sides of a triangle be (3, -2), (-3, 1), and (4, -3), then find the coordinates of its vertices.
Solution:
In a ∆ABC,
D, E and F are the mid-points of the sides BC, CA and AB respectively and co-ordinates of D, E and F are (3, -2), (-3, 1) and (4, -3) respectively.

Assume the coordinates of A are (x1, y1), of B are (x2, y2) and of C are (x3, y3)
Now,
As D is the mid-point BC
Therefore,
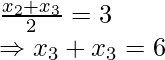
and
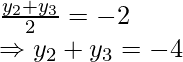
As E is the mid-point of CA
Therefore,
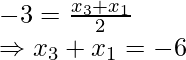
and
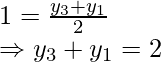
and F is the mid-point of AB
Therefore,
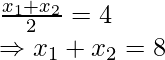
and
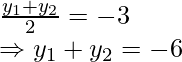
Now,
x2 + x3 = 6 ……..(i)
x3 + x1 = -6 ……..(ii)
x1 + x2 = 8 ………(iii)
On adding we get
2(x1 + x2 + x3) = 8
⇒ x1 + x2 + x3 = 4 …….(iv)
On subtracting from (iv) we get
x1 = -2,
x2 = 10,
x3 = -4
and
y2 + y3 = -4 …….(v)
y3 + y1 = 2 …….(vi)
y1 + y2 = -6 ………(vii)
On Adding, We will get
2(y1 + y2 + y3) = -8
⇒ y1 + y2 + y3 = -4 ……..(viii)
On subtracting from (viii) we get
y1 = 0,
y2 = -6,
y3 = 2
Hence, the coordinates of A are (-2, 0) of B are (10, -6) and of C (-4, 2).
Question 52. The line segment joining the points (3, -4) and (1, 2) is trisected at the points P and Q. If the co-ordinates of P and Q are (p, -2) and (53 , q) respectively, find the values of p and q.
Solution:
Assume line AB whose ends points are A (3, -4) and B (1, 2)

Coordinates of P and Q which trisect AB are P (p, -2) and Q 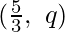
Now,
As P divides AB in the ratio 1 : 2
Therefore,
Coordinates of P will be
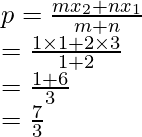
Similarly, Q divides AB in the ratio 2 : 1
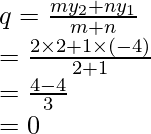
Hence,
p = 7/3, q = 0
Question 53. The line joining the points(2, 1), (5, -8) is trisected at the points P and Q. If point P lies on the line 2x – y + k = 0, find the value of k.
Solution:
Points A (2, 1), and B (5, -8) are the ends points of the line segment AB

Points P and Q trisect it and P lies on the line 2x – y + k = 0
As P divides AB in the ratio of 1 : 2
Therefore,
Coordinates of P will be
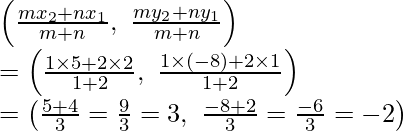
Therefore,
Coordinates of P are (3, -2)
As it lies on 2x – y + k = 0
Therefore,
It will satisfy it
2 × 3 – (-2) + k = 0
⇒ 6 + 2 + k = 0
⇒ 8 + k = 0
⇒ k = -8
Question 54. A (4, 2), B (6, 5), and C (1, 4) are the vertices of ∆ABC,
(i) The median from A meets BC in D. Find the coordinates of the point D.
(ii) Find the coordinates of point P on AD such that AP : PD = 2 : 1.
(iii) Find the coordinates of the points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What do you observe?
Solution:
In ∆ABC, co-ordinates of A (4, 2) of (6, 5) and of (1, 4) and AD is BE and CF are the medians
such that D, E and F are the mid-points of the sides BC, CA and AB respectively
P is a point on AD such that AP : PD = 2 : 1

(i) Now coordinates of D will be
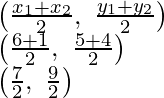
(ii) As P divides AD in the ratio of 2 : 3
Therefore,
Coordinates of P will be
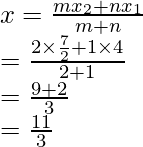
Thus,
Coordinates of P are 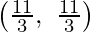
(iii) As E and F are the mid-point if CA and AB respectively
Coordinates of E will be
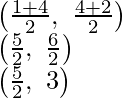
and of F will be
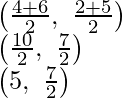
As Q and R divides BE and CF in such a way that BQ : QE = 2 : 1 and CR : RF = 2 : 1
Therefore,
Coordinates of Q will be
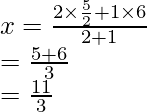
and
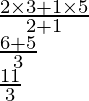
i.e., Q1 is (11/3, 11/3)
and similarly the coordinates of R will be
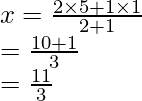
and
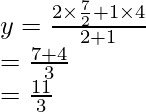
R is (11/3, 11/3)
(iv) We can see that coordinates of P, Q and R are same
i.e., P, Q and R coincides each other.
Medians of the sides of a triangle pass through the same point which is called the centroid of the triangle.
Question 55. If the points A (6, 1), B (8, 2), C (9, 4), and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
Solution:
The diagonals of a parallelogram bisect each other
O is the mid-point of AC and also of BD
O is the mid-point of AC

Therefore,
Coordinates of O will be
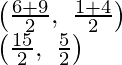
As O is also the mid-point of BD
Therefore,

and
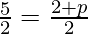
⇒ 8 + k = 15
⇒ k = 15 – 8 = 7
and
⇒ 2 + p = 5
⇒ p = 5 – 2 = 3
Hence,
k = 7, p = 3
Question 56. A point P divides the line segment joining the points A (3, -5) and B (-4, 8) such that 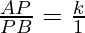 . If P lies on the line x + y = 0, then find the value of k.
. If P lies on the line x + y = 0, then find the value of k.
Solution:
Point P divides the line segment by joining the points A (3, -5) and B (-4, 8)
Such that 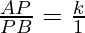
⇒ AP : PB = k : 1
Assume coordinates of P be (x, y), then
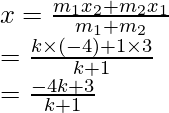
and
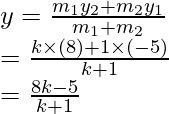
As x + y = 0
Therefore,
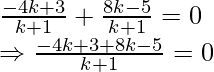
4k – 2 = 0
4k = 2
k = 2/4
k = 1/2
Question 57. The mid-point P of the line segment joining the points A (-10, 4) and B (-2, 0) lies on the line segment joining the points C (-9, -4) and D (-4, y). Find the ratio in which P divides CD. Also, find the value of y.
Solution:
P is the mid-point of line segment joining the points A (-10, 4) and B (-2, 0)
Coordinates of P will be
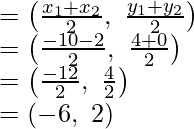
P lies on CD also,
Let P divides C (9, 4) and D (-4, y) in the ratio m1 : m2
Therefore,
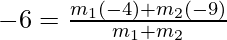
⇒ -6m1 – 6m2 = -4m1 – 9m2
⇒ -6m1 + 4m1 = -9m2 + 6m2
⇒ -2m1 = -3m2
⇒ 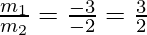
Therefore,
m1 : m2 = 3 : 2
and
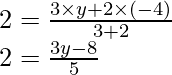
⇒ 10 = 3y – 8x
⇒ 3y = 10 + 8 = 18
⇒ y = 18/3 = 6
⇒ y = 6
Question 58. If the point C (-1, 2) divides internally the line segment joining the points A (2, 5) and B (x, y) in the ratio 3 : 4, find the value of x2 + y2.
Solution:
As we know that if a point (x, y) divides the line segment joining
the points (x1, y1) and (x,2 y2) in the ration m : n, then
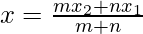
and
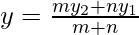
Now here, C (-1, 2) divides the line segment joining A (2, 5) and B (x, y) in the ratio of 3 : 4
Now,
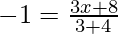
and
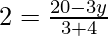
⇒ 3x + 8 = -7
and
⇒ 20 – 3y = 14
⇒ x = -5
and
⇒ y = 2
Now,
x2 + y2 = (-5)2 + (2)2
x2 + y2 = 25 + 4 = 29
Question 59. ABCD is a parallelogram with vertices A (x1, y1), B (x2, y2), and C (x3, y3). Find the coordinates of the fourth vertex D in terms of x1, x2, x3, y1, y2, and y3
Solution:
Assume the coordinates of D be (x, y). We know that diagonals of a parallelogram bisect each other.

Hence,
Mid-point of AC = Mid-point of BD
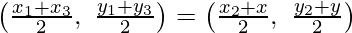
i.e., x1 + x3 = x2 + x and y1 + y3 = y2 + y
i.e, x1 + x3 – x2 = x and y1 + y3 + y2 = y
Hence, the coordinates of D are (x1 + x3 – x2, y1 + y3 + y2)
Question 60. The points A (x1, y1), B (x2, y2), and C (x3, y3) are the vertices of ∆ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the points of coordinates Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What are the coordinates of the centroid of the triangle ABC?
Solution:
Given: The points A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of ∆ABC.
(i) We know that, the median bisect the line segment into two equal parts i.e., here D is the mid-point of BC.
Therefore,
Coordinates of mid-point of BC = 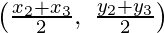
D = 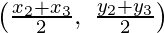
(ii) Assume the coordinates of a point P be (x, y)
Given that, the point P (x, y), divide the line joining A (x1, y1) and
D 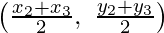 in the ration of 2 : 1,
in the ration of 2 : 1,
Then the coordinates of P
![Rendered by QuickLaTeX.com =\left[\frac{2\left(\frac{x_2+x_3}{2}\right)+1.x_1}{2+1},\ \frac{2\left(\frac{y_2+y_3}{2}\right)+1.y_1}{2+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5559f20fc7bc55e2d64a06efbddcf672_l3.png)

Using internal section formula, we get
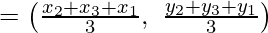
Therefore,
Required coordinates of points P = 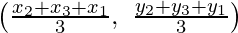
(iii) Assume the coordinates of a point Q be (p, q)
Given: The point Q (p, q) divide the line joining B(x2, y2) and E 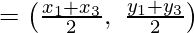
In the ratio of 2 : 1
Then the coordinates of Q

![Rendered by QuickLaTeX.com =\left[\frac{2\left(\frac{x_1+x_3}{2}\right)+1.x_2}{2+1},\ \frac{2\left(\frac{y_1+y_3}{2}\right)+1.y_2}{2+1}\right]\\ \left(\frac{x_2+x_3+x_1}{3},\ \frac{y_2+y_3+y_1}{3}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ceb17107b0896af61e06f9a9f5902439_l3.png)
[Since, BE is the median of side CA. So, BE divides AC into two equal parts]
Therefore,
Mid-point of AC = Coordinates of E
⇒ E = 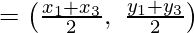
So, the required coordinate of point Q = 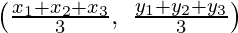
Now, let us considered that the coordinates of a point E be (α, β).
It is given that, the point R (α, β), divide the line joining C (x3, y3) and
F 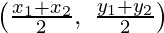 in the ration 2 : 1,
in the ration 2 : 1,
So, the coordinates of R be
![Rendered by QuickLaTeX.com =\left[\frac{2\left(\frac{x_1+x_2}{2}\right)+1.x_3}{2+1},\ \frac{2\left(\frac{y_1+y_2}{2}\right)+1.y_3}{2+1}\right]\\ \left(\frac{x_2+x_3+x_1}{3},\ \frac{y_2+y_3+y_1}{3}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2eebab6864f4ea04173b66c24a708aed_l3.png)
Here, CF is the median of side AB, hence CF divides AB into two equal parts
Hence,
Mid-point of AB = Coordinates of CF
⇒ F 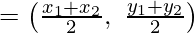
So, required coordinate of point R 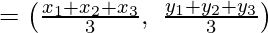
(iv) Coordinate of the centroid of the ∆ABC = (sum of abscissa of all vertices/3, sum of all vertices/2)
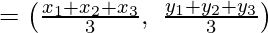
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...