Question 1. Find the coordinates of the point which divides the line segment joining (-1, 3) and (4, – 7) internally in the ratio 3: 4.
Solution:
Assume P(x, y) be the needed point.
After applying the Section Formula,
As we know that here the coordinates are
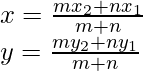
Now here we have,
x1 = – 1
y1 = 3
x2 = 4
y2 = -7
m : n = 3 : 4
Thus,

Hence,
The coordinates of P are (8/7, -9/7)
Question 2. Find the points of trisection of the line segment joining the points:
(i) (5, – 6) and (-7, 5)
(ii) (3, – 2) and (-3, – 4)
(iii) (2, – 2) and (-7, 4)
Solution:
(i) Assume P and Q are the points of trisection for AB
Thus,
AP = PQ = QB

Thus,
P divides AB within in the ratio of 1 : 2,
After putting in Section Formula,
The coordinates of P are

After this,
Q also divides AB within in the ratio of 2 : 1.
Hence, their coordinates are
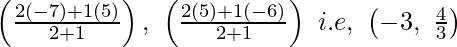
(ii) Assume P and Q are the points of trisection of AB i.e., AP = PQ = QB

Thus, P divides AB within in the ratio of 1 : 2.
Therefore, after putting in the Section Formula,
The coordinates of P are
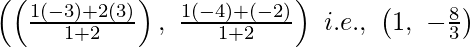
After this,
Q also divides as within in the ratio of 2 : 1
Thus, the coordinates of Q are shown as
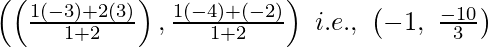
(iii) Assume P and Q are the points of the trisection of AB
i.e., AP = PQ = OQ

As, P divides AB within in the ratio 1 : 2.
Thus, the coordinates of P, by putting in the Section Formula, are shown as
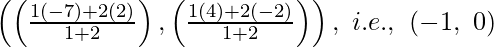
After this,
Q also divides AB putting in the ration 2 : 1.
Thus, the coordinates of Q are shown as
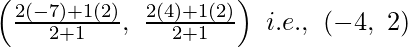
Question 3. Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (-2, -1), (1, 0), (4, 3), and (1, 2) meet.
Solution:

Assume: A(-2, -1), B(1, 0), C(4, 3) and D(1, 2) are the given points.
Assume P(x, y) is the point of intersection of the diagonals of the
parallelogram as formed by the given points. as shown in the fig.
As we know that, the diagonals of a parallelogram bisect each other.
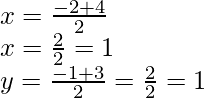
Hence,
The coordinates of P are (1, 1).
Question 4. Prove that the points (3, 2), (4, 0), (6, -3), and (5, -5) are the vertices of a parallelogram.
Solution:

Assume: A(3, -2), B(4, 0), C(6, -3) and D(5, -5)
Assume P(x, y) is the point of intersection of diagonals AC and BD of ABCD. As shown in the fig.
Now, the mid-point of AC is shown as,
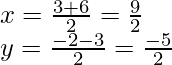
Mid – point of AC 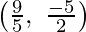
Now again, the mid-point of BD is shown as,
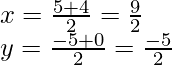
Thus, suppose that diagonals AC and BD bisect each other.
Also, as we know that diagonals of a parallelogram bisect each other.
Hence,
ABCD is a parallelogram.
Question 5. If P(9a – 2, -b) divides the line segment joining A(3a + 1, -3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
Solution:
Given: P(9a – 2, -b) divides the line segment joining A(3a + 1, -3) and B(8a, 5) in the ratio 3 : 1
After applying Section Formula
Coordinates of P are
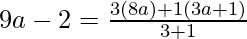
And,
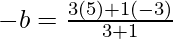
Now, lets solve for a, we will have
(9a – 2) × 4 = 24a + 3a + 1
36a – 8 = 27a + 1
9a = 9
a = 1
Now, lets solve for b, we will have
4x – b = 15 – 3
-4b = 12
b = -3
Hence,
The values of a and b are 1 and -3 respectively.
Question 6. If (a, b) is the mid-point of the line segment joining the points A (10, -6), B(k, 4), and a – 2b = 18, find the value of k and the distance AB.
Solution:
Given: (a, b) is the mid-point of the line segment A(10, -6) and B(k, 4)
Thus,
(a, b) = 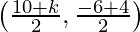
a =  and b = -1
and b = -1
2a = 10 + k
k = 2a – 10
Given, a – 2b = 18
Apply b = -1 above we will get,
a – 2(-1) = 18
a = 18 – 2 = 16
Since,
k = 2(16) – 10 = 32 – 10 = 22
Therefore,
AB = 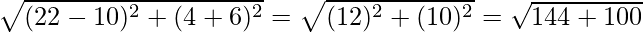 = 2√61 units
= 2√61 units
Question 7. Find the ratio in which the point (2, y) divides the line segment joining the points A(-2, 2) and B(3, 7). Also, find the value of y.
Solution:
Assume: Point P(2, y) divide the line segment joining the points A(-2, 2) and B(3, 7) in the ratio k : 1
Thus, the coordinates of P will be given by
![Rendered by QuickLaTeX.com \left[\frac{3k+(-2)\times1}{k+1},\ \frac{7k+2\times1}{k+1}\right]\\ =\left[\frac{3k-2}{k+1},\ \frac{7k+2}{k+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d525117daf62d2129e9497387bcc42f_l3.png)
Also, given the coordinates of P are (2, y)
So,
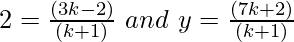
Thus, solving for k, we will get
2(k + 1) = (3k – 2)
2k + 2 = 3k – 2
k = 4
Now use the value of k to find y,
we have
y = 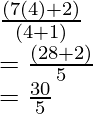
y = 6
Hence,
The ratio 4 : 1 and y = 6
Question 8. If A(-1, 3), B(1, -1) and C(5, 1) are the vertices of a triangle ABC, find the length of the median through A.
Solution:

Assume AD is the median through A.
Such that, AD is the median, D is the mid-point of BC
Thus,
The coordinates of D  are = (3 , 0)
are = (3 , 0)
Therefore,
The length of median AD = 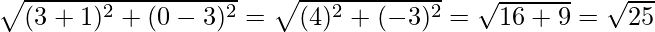 = 5 units
= 5 units
Question 9. If the points P, Q(x, 7), R, S(6, y) in this order divide the line segment joining A(2, p) and B (7, 10) in 5 equal parts, find x, y, and p.
Solution:

Given: AP = PQ = QR = RS = SB
Since,
Q is the mid-point of A and S
Then,
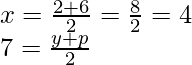
y + p = 14 ….. (i)
Thus,
Since S divides QB in the ratio 2 : 1
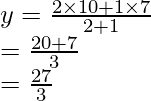 = 9
= 9
Therefore,
p = 14 – 9 = 5
Hence,
x = 4,
y = 9
and
p = 5
Question 10. If a vertex of a triangle be (1, 1) and the middle points of the sides through it be (-2, 3) and (5, 2) find the other vertices.
Solution:
Assume, A(1, 1) is the given vertex and
D(-2, 3), E(5, 2) be the mid-points of AB and AC
So, D and E are the mid-points of AB and AC
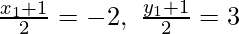
x1 + 1 = 4
x1 = -5
y1 + 1 = 6
y1 = 5
Thus, the coordinates of B are (-5, 5)
Now,

x2 + 1 = 10
x2 = 9
y2 + 1 = 4
y2 = 3
Hence,
The coordinates of C are (9, 3)
Hence,
The other vertices of the triangle are (-5, 5) and (9, 3).
Question 11 (i). In what ratio is the segment joining the points (-2, -3) and (3, 7) divides by the y-axis? Also, find the coordinates of the point of division.
Solution:
Assume P(-2, -3) and Q(9, 3) be the given points.
Assume y-axis divides PQ in the ratio k : 1 at R(0, y)
Thus, the coordinates of R are shown by

After, equating
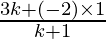
= 0
3k – 2 = 0
k = 2/3
Hence,
The ratio is 2 : 3
After putting k = 2/3 in the coordinates of R, we will get
R (0, 1)
Question 11 (ii). In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, -21/5)?
Solution:
Assume A(-3, -1) and B(-8, -9) are the given points.
And,
Assume P be the point that will divide AB in the ratio of k : 1
Thus, the coordinates of P can be shown by

Therefore, given coordinates of P
After equating, we will get
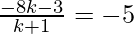
-8k – 3 = -5k – 5
3k = 2
k = 2/3
Hence, the point P divides AB in the ratio 2 : 3
Question 12. If the mid-point of the line joining (3, 4) and (k, 7) is (x, y) and 2x + 2y + 1 = 0 find the value of k.
Solution:
Since, (x, y) is the mid-point
x = (3 + k)/2 and y = (4 + 7)/2 = 11/2
Given: Mid-point lies on the line 2x + 2y + 1 = 0
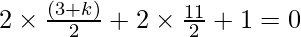
3 + k + 11 + 1 = 0
Therefore,
k = -15
Question 13. Find the ratio in which the point P(3/4, 5/12) divides the line segments joining the point A(1/2, 3/2) and B(2, -5).
Solution:
Given: Points A(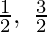 ) and B(2, -5)
) and B(2, -5)
Assume the point P(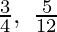 ) and divide the line segment AB into the ratio of k : 1
) and divide the line segment AB into the ratio of k : 1
Thus, as we know that
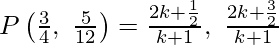
Hence, we will equate the abscissa we will get;
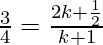
3(k + 1) = 4(2k + 1/2)
3k + 3 = 8k + 2
5k = 1
k = 1/5
Hence,
The point P(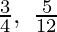 ) divides in ratio of 1 : 5.
) divides in ratio of 1 : 5.
Question 14. Find the ratio in which the line joining (-2, -3) and (5, 6) is divided by
(i) x-axis
(ii) y-axis
Also, find the coordinates of the point of division in each case.
Solution:
Assume A(-2, -3) and B(5, 6) are the given points.
(i) Assume x-axis divides AB in the ratio of k : 1 at the point P.
Hence, the coordinates of the point of division are shown as,
![Rendered by QuickLaTeX.com \left[\frac{5k-2}{k+1},\ \frac{6k-3}{k+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-364ad9d94f5e56aafca0f0288c701d40_l3.png)
Thus, P lies in the x-axis,
The y – coordinate is zero.
Therefore,
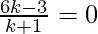
6k – 3 = 0
k = 1/2
Therefore,
Required ratio is 1 : 2
Applying value of k in the coordinates of P
We will get, P 
(ii) Assume y-axis divides AB in the ratio of k : 1 at the point Q.
Hence, the coordinates of the point of division are shown as,
![Rendered by QuickLaTeX.com \left[\frac{5k-2}{k+1},\ \frac{6k-3}{k+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-364ad9d94f5e56aafca0f0288c701d40_l3.png)
Thus, Q lies on the y-axis,
The x – ordinate is zero.
Therefore,

Therefore,
Required ratio is 2 : 5
Applying the value k in the coordinates of Q
We will get, Q 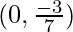
Question 15. Prove that the points (4, 5), (7, 6), (6, 3), (3, 2) are the vertices of a parallelogram. Is it a rectangle?
Solution:

Assume A (4, 5), B(7, 6), C(6, 3) and D(3, 2) are the given points, as shown in the fig
And,
Let the point P be the point of intersection of AC and BD.
Mid-point of AC coordinates are  = (5, 4)
= (5, 4)
Mid-point of BD coordinates are 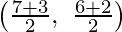 = (5, 4)
= (5, 4)
Therefore, we can see that the mid-point of AC and BD are same.
Hence,
ABCD is a parallelogram.
Now,
AC =  = √8 units
= √8 units
and,
BD = 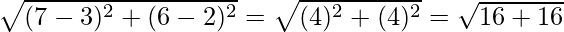 = √32 units
= √32 units
Therefore,
AC ≠ BD
Hence, ABCD is not a rectangle.
Question 16. Prove that (4, 3), (6, 4), (5, 6), and (3, 5) are the angular points of a square.
Solution:

Assume A(4, 3), B(6, 4), C(5, 6), and D(3, 5) are the given points, as shown in the figure.
By applying Distance Formula:
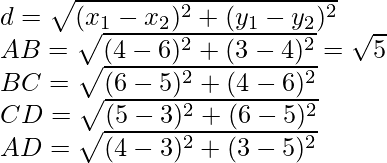
We can see that the length of all the sides are same.
Now,
The length of diagonals are;
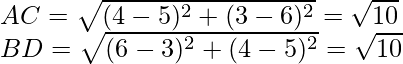
The length of both the diagonals are same.
Hence, we can say that the given points are the angular points of a square.
Question 17. Prove that the points (-4, -1), (-2, -4), (4, 0), and (2, 3) are the vertices of a rectangle.
Solution:

Assume A(-4, -1), B(-2, -4), C(4, 0) and D(2, 3) are the given points.
Now,
Mid-point of AC coordinates are 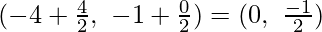
Mid-point of BD coordinates are 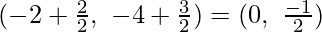
Hence,
We can see that AC and BD have the same point.
And,
Now for the diagonals
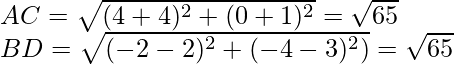
Thus length of diagonals are also same.
Hence, the given points are the vertices of a rectangle.
Question 18. Find the length of the medians of a triangle whose vertices are A(-1, 3), B(1, -1), and C(5, 1).
Solution:

Assume AD, BF and CE are the medians of ΔABC
Coordinates of D are  = (3, 0)
= (3, 0)
Coordinates of E are 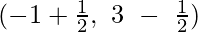 = (0, 1)
= (0, 1)
Coordinates of F are 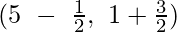 = (2, 2)
= (2, 2)
Now,
Obtaining the length of the respectively medians:
Length of AD = 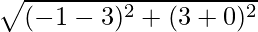 = 5 units
= 5 units
Length of BF = 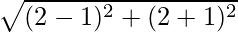 = 10 units
= 10 units
Length of CE = 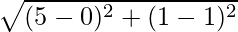 = 5 units
= 5 units
Question 19. Find the ratio in which the line segment joining the points A (3, -3) and B (-2, 7) is divided by x- axis. Also, find the coordinates of the point of division.
Solution:
Assume the point on the x-axis be (x, 0). {y – coordinate is zero}
And,
Allow this point to divide the line segment AB in the ratio of k : 1.
After applying the Section Formula for the y-coordinate,
we will get
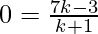
7k – 3 = 0
k = 3/7
Hence, x – axis divides the line segment AB in the ratio of 3 : 7.
Question 20. Find the ratio in which the point P(x, 2) divides the line segment joining the points A (12, 5) and B (4, -3). Also, find the value of x.
Solution:
Assume P divide the line joining A and B
and
Allow it to divide the segment in the ratio of k : 1
After applying the Section Formula for the y – coordinate
we will get
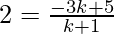
2(k + 1) = -3k + 5
2k + 2 = -3k + 5
5k = 3
k = 3/5
Therefore,
The line segment AB is divided by P in the ratio of 3 : 5
By applying the value of k,
We will get the x – coordinate as
x = 12 + 60/8 = 72/8 = 9
Hence, the coordinates of point P is (9, 2).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...