Class 10 RD Sharma- Chapter 15 Areas Related to Circles – Exercise 15.3
Last Updated :
18 Mar, 2021
Question 1. AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
Solution:
Given,
Radius of the circle with centre O, given by OA and OB = r = 4 cm
Also, length of the given chord AB = 4 cm
Since all the sides are equal, OAB is an equilateral triangle where the angle AOB = 60°

Thus, the angle subtended at the centre θ is equal to 60°
Now,
Area of the minor segment = (Area of sector) – (Area of triangle AOB)
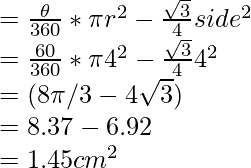
Therefore, now the required area of the segment is given by (8π/3 – 4√3) cm2
Question 2. A chord PQ of length 12 cm subtends an angle 120o at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
Solution:
We have, ∠POQ = 120o and the line segment PQ = 12 cm
Draw the line segment OV ⊥ PQ,

Now,
PV = PQ × (0.5) = 12 × 0.5 = 6 cm
Since, ∠POV = 120o
Also,
∠POV = ∠QOV = 60o
We have,
In triangle OPQ, we have
Sin θ = PV/ OA
Sin 60o = 6/ OA
Substituting the values, we get,
√3/2 = 6/ OA
OA = 12/ √3 = 4√3 = r
Now, calculating the area of the minor segment
Area of the segment = area of sector OPUQO – area of △OPQ
= θ/360 x πr2 – ½ x PQ x OV
= 120/360 x π(4√3)2 – ½ x 12 x 2√3
= 16π – 12√3 = 4(4π – 3√3)
Hence,
Area of the minor segment = 4(4π – 3√3) cm2
Question 3. A chord of a circle of radius 14 cm makes a right angle at the centre. Find the areas of the minor and major segments of the circle.
Solution:
Given,
Radius (r) of the circle is given by = 14 cm
Angle subtended by the chord with the centre of the circle, θ is given by 90°

Now,
Area of minor segment = θ/360 x πr2 – ½ x r2 sin θ
Substituting the values, we get,
= 90/360 x π(14)2 – ½ x 142 sin (90°)
= ¼ x (22/7) (14)2 – 7 × 14
= 56 cm2
Area of circle = πr2
Substituting the values,
= 22/7 x (14)2 = 616 cm2
Thus, we know,
The area of the major segment = Area of circle – Area of the minor segment
= 616 – 56 = 560 cm2
Question 4. A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both the segments.
Solution:
Given,
Radius of the circle, r = 5√2 cm = OA = OB
Length of the chord AB = 10 cm

Now,
In triangle OAB,
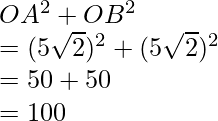
AB2 = 100
Thus, Pythagoras theorem is satisfied, that is, OAB is a right-angled triangle.
Angle subtended by the chord at the centre of the circle, θ = 90°
We know,
Area of minor segment = area of sector – area of triangle
Substituting the values,
= θ/360 × πr2 – ½ x r2 sin θ
= 90/360 × (3.14) 5√22 – ½ x (5√2)2 sin 90
= [¼ x 3.14 x 25 x 2] – [½ x 25 x 2 x 1]
We obtain,
= 25(1.57 – 1)
= 14.25 cm2
Area of circle = πr2 = 3.14 x (5√2)2 = 3.14 x 50 = 157 cm2
Thus,
Area of major segment = Area of circle – Area of minor segment
= 157 – 14.25
= 142.75 cm2
Question 5. A chord AB of circle of radius 14 cm makes an angle of 60° at the centre of a circle. Find the area of the minor segment of the circle.
Solution:
Given,
Radius of the circle (r) is given by= 14 cm = OA = OB
Angle subtended by the chord at centre of the circle, θ = 60°

In triangle AOB, since, angle opposite to equal sides are equal,
Therefore, angle A = angle B
By angle sum property,
∠A + ∠B + ∠O = 180
x + x + 60° = 180°
2x = 120°, x = 60°
Since, all the angles are 60° each, therefore, the triangle OAB is an equilateral with OA = OB = AB
We know,
Area of the minor segment = area of sector – area of triangle OAB
= θ/360 × πr2 – 1/2 r2 sin θ
= θ/360 × πr2 – 1/2 x (14)2 sin 60°
= 60/360 × (22/7) 142 – 1/2 x (14)2 x √3/2
= 60/360 x (22/7) 142 – √3/4 x (14)2
= 142 [(1/6) x (22/7)] – 0.4330
= 142 [(22/42)] – 0.4330
= 142 [(11-9.093)/21]
= 142 [0.09080]
= 17.79
Therefore, the area of the minor segment = 17.79 cm2
Question 6. Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°. [Ncert Exemplar]
Solution:
We have,
Radius of the circle, r = 14 cm
Central angle of the corresponding sector = 60°
Since, OA = OB = r, therefore, triangle AOB is an isosceles triangle.

∠OAB = ∠OBA = θ
Now, in triangle OAB, by angle sum property
∠AOB + ∠OAB + ∠OBA = 180°
Substituting values,
60° + θ + θ = 180°
Solving,
θ = 60°
Now, since all the angles are equal , therefore it is an equilateral triangle, with equal sides, that is,
OA = OB = AB = 14 cm
Area of triangle OAB = 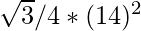
Substituting the values, we get
Area = 49 √3 cm2
Also,
Area of sector OBAO = 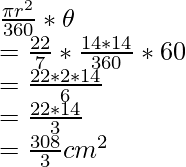
Now,
Area of minor segment = Area of sector OBAO – Area of triangle OAB = 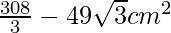
Question 7. A chord of a circle of radius 20 cm subtends an angle of 90° at the centre. Find the area of the corresponding major segment of the circle. (Use π = 3.14) [Ncert Exemplar]
Solution:
Let AB be the chord of a circle of radius 10 cm, with O as the centre of the circle

We know,
∠AOB = 90°
Therefore,
Angle of the major sector = 360° – 90° = 270°
Therefore,
Area of the major sector =
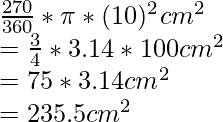
Now,
Draw OM perpendicular to AB
So,
AM = 1/2 AB and ∠AOM = 1/2×90° = 45°
Now,
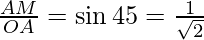
So,
AM = 10/√2
Therefore, AB = 10√2 cm and also, OM=OA
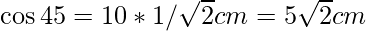
So,
Area of triangle OAB = 1/2 * base * height
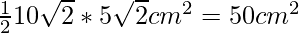
Area of the required major segment = 235.5 cm2 + 50 cm2 = 285.5 cm2
Also,
Area of triangle OAB = 1/2 × OA × OB
= 1/2 × 10 × 10 cm2 = 50 cm2
Question 8. The radius of a circle with centre O is 5 cm (see figure). Two radii OA and OB are drawn at right angles to each other. Find the areas of the segments made by the chord AB (Take π = 3.14).

Solution:
Radius of the circle ,r = 5 cm
Since, OA and OB are at right angle
Therefore, ∠AOB = 90°
∵ Chord AB makes two segments which are minor segment and major segment respectively.
Now,
Area of the minor segment
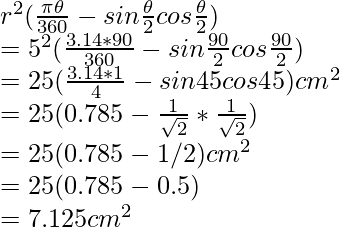
Area of circle = pi * r2 = 78.50 cm2
Therefore, area of major segment = 71.375 sq. units.
Question 9. AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 0. The area of the minor segment cut off by AC is equal to twice the area of the sector BOC. Prove that.
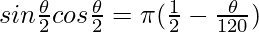
Solution:

Given,
∠AOC = 180° – θ
Let us assume r to be the radius of the circle.

Area of sector BOC = 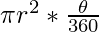
Now,
Area of minor segment AC = 2 * Area of sector BOC
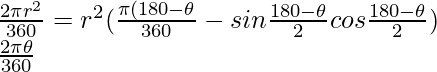
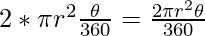
But, Area of segment=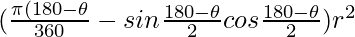
Now, 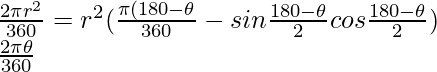
Also,
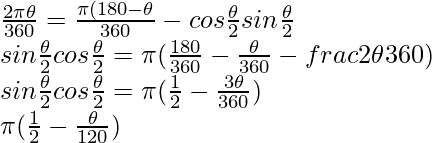
Question 10. A chord of a circle subtends an angle of 0 at the centre of the circle. The area of the minor segment cut off by the chord is one eighth of the area of the circle. Prove that
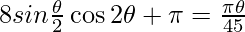
Solution:
Let chord AB subtends an angle of 0° at the centre of a circle with radius r
Now area of the circle = nr1 and area of the minor segment ACB.

But.
Area of the minor segment ACB = 1/8 = area of circle
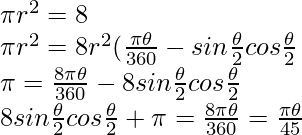
Share your thoughts in the comments
Please Login to comment...